МБОУ СОШ №1 г. Покров Петушинского района Владимирской области

Петрушкина Ольга Константиновна

Учитель высшей квалификационной категории

Освоение таблицы умножения в начальных классах.

Особое место в программе математики в начальной школе отводится таблице умножения. Практикующие учителя знают, что при ее изучении у детей развиваются познавательные процессы, произвольное внимание, математическая речь. Учитывая прописанные в новом образовательном стандарте цели обучения, изучение действия умножения должно работать на общее развитие учащихся – развивать их интеллект, волю, возбуждать интерес к познанию. Поэтому заучивание таблицы умножения должно быть осознанным, а не механическим.

В 2 классе учащиеся получают понятие об умножении и знакомятся с действиями умножения и деления в пределах 20. Лучшему осознанию учащимся смысла действия умножения способствует подготовительная работа: счет равными группами предметов, а также счет по 2, 3, 4, 5, до 20.

Нужно обратить внимание на принципы построения таблиц умножения. При построении таблиц умножения нужно обратить внимание детей на закономерность в числах, являющихся значениями произведений: каждое следующее число больше предыдущего на определенное число, равное первому множителю. Эту закономерность можно изобразить в виде прыжков по числовому лучу.

Для запоминания таблицы умножения существуют такие приемы как:

- прием счета двойками, тройками, пятерками;

- прием последовательного сложения – основной прием получения результатов табличного умножения.

Данный прием связан со смыслом действия умножения как сложения одинаковых слагаемых;

- прием прибавления слагаемого к предыдущему результату (вычитания из предыдущего результата).

Данный прием, является вторым основным приемом получения результатов табличного умножения. Используется в том случае, если ребенок смог выучить хотя бы несколько случаев из каждой таблицы. Это могут быть 3-4 первых самых легких случая, или 2-3 наиболее запоминающихся случая.

- прием взаимосвязанной пары: 2*6 6*2 (перестановка множителей);

При хорошем понимании правила перестановки множителей ребенок заучивает в два раза меньше случаев табличного умножения, чем содержит полная таблица. Используя перестановку множителей, все остальные случаи можно получить из имеющихся.

- прием запоминания последовательности случаев с ориентиром на возрастание второго множителя;

Этот прием активно реализован в традиционном учебнике по математике для 2 и 3 классов, где табличные случаи предлагаются ребенку на уроке «серией»:

3*2 3*3 3*4 3*5

Эту же «серию» учитель предлагает детям для заучивания к следующему уроку. На следующем уроке изучается новая «серия»:

3*6 3*7 3*8 3*9

Эта же «серия» предлагается детям для заучивания.

- прием «порции»;

Этот прием активно реализован в учебнике математики для 2 и 3 классов автора Н.Б. Истоминой. Для заучивания ребенку предлагается «порция», состоящая из 2-3 случаев, но не по принципу возрастания второго множителя.

Например, «порция» состоит из трех случаев: 9 * 5; 9 * 6; 9 * 7. Первым для заучивания предлагается случай 9 * 6, а от него, используя прием 3, ребенок переходит к случаям 9*5 и 9*7. В следующий раз «порция» снова содержит три случая 9 * 4; 9 * 3; 9 * 2. Здесь опорным случаем является случай 9 * 3.

- прием запоминающегося случая в качестве опорного.

Например, 5*6 =30, значит 5*7 =30+5 =35;

- прием внешней опоры;

В качестве опоры используется рисунок или прямоугольная таблица чисел. Детям, которые обладают плохой механической памятью, можно па первых порах предложить использовать клетчатое поле тетради. Обводя на клетчатом поле прямоугольник с заданным количеством клеток в сторонах, ребенок использует эту модель для контроля полученного результата или просто подсчитывает клетки как умеет. Например:

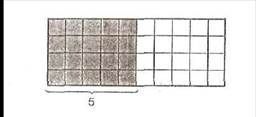4 * 5 = 20

-графический способ умножения.

Например, 2X3 =6 -для этого рисуются 3 вертикальных линии и 2 горизонтальные линии так, чтобы они пересекались Количество точек пересечения –результат произведения.

- прием запоминания таблицы «с конца»;то есть самых сложных случаев, а простые он может получить сложением одинаковых слагаемых.

- пальцевый счет при запоминании таблицы умножения.

Например, нужно умножить 6 на 7. Зажимаем пальцы на обеих руках в кулак, а затем на каждой руке отгибаем столько пальцев, на сколько каждый множитель больше, чем пять. На двух руках отогнуто три пальца - это число десятков в искомом числе. На одной руке остались прижатыми к ладони три пальца, на другой – четыре пальца. Эти числа перемножаем 3 * 4 = 12 и прибавляем к числу имеющихся десятков. 30 + 12 = 42. Ответ: 6 * 7 = 42.

Умножение на 9

Снова поверните кисти ладонями к себе, но теперь нумерация пальцев будет идти по порядку с лева на право, то есть от 1 до 10.

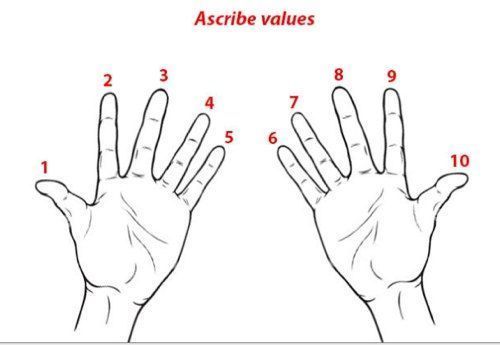
Теперь умножаем, например, 2х9. Все то, что идет до пальца №2 — это десятки (то есть 1 в этом случае). А все то, что остается после пальца №2 – единицы (то есть 8). В итоге получаем 18.

Плюсы данного способа - наглядность.

Минусы – при устном счете каждый раз к рисунку – потеря времени.

Этот секрет работает только в таблице на 9.

1 10-1 9

2 20-2 18

3 30-3 27

4 40-4 36

5 50-5 45

6 60-6 54

7 70-7 63

8 80-8 72

9 90-9 81

Полезно также ставить вопросы, отвечая на которые, дети открывают для себя практическую пользу от таблиц умножения.

Сколько глаз у пяти человек?

Сколько ног у семи воробьев?

Сколько ушей у восьми кошек?

Сколько ног у пяти собак?

В каких случаях тебе помогла ответить таблица умножения на 2?

Какую таблицу умножения нужно знать, чтобы ответить на последний вопрос?

Выполни действия

3*4 6*4 30*6 6*3 3*5 6*5 6*6 6*8 3*7 6*7 3*9 6*9 3*12 3*30

Подчеркни те равенства, с которыми связаны следующие задачи:

В одни сани запрягают трех лошадей. Сколько нужно запрячь лошадей в пять саней?

У одного жука шесть ног. Сколько ног у четырех жучков? А у шести?

Сколько углов у четырех треугольников? А у семи?

Тетрадь стоит шесть рублей. Сколько будут стоить восемь таких тетрадей? А девять?

Верно построенная работа помогает ученикам справиться даже с таким сложным материалом, как освоение таблицы умножения.

Список литературы

1. Программы и учебники математики начальной школы, методические пособия для учителя, дидактические материалы для учащихся.

2. Актуальные проблемы методики обучения математике в начальных классах/ Под ред.М.И. Моро, А.М. Пышкало.- М.,1987.

3. Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в начальных классах.- М., 1984.

4. Беспалько В.П. Педагогика и прогрессивные технологии обучения.- М.: Изд-во Ин-та профобразования Минобразования России, 1995.

5. Истомина Н.Б. и др. Методика преподавания математики в начальных классах.- М.: МГЗПИ, 1996.

7. Жикалкина Т.К. Дидактические игры на уроках математики.- М., 1994.