«Формула суммы n первых членов арифметической прогрессии»




 Муниципальное
бюджетное общеобразовательное учреждение
Муниципальное
бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №1 имени Н. Л. Мещерякова
г. Зарайск
Конспект открытого урока
в 9 классе
«Формула суммы n первых членов арифметической прогрессии»
подготовила учитель
первой квалификационной
категории
Авдюхина Л.А.
2013-2014 учебный год
Цель: обеспечить усвоение учащимися формул суммы n первых
членов арифметической прогрессии, решение задач по теме
Задачи:
- обеспечить усвоение учащимися формул суммы n первых членов арифметической прогрессии; формирование умений и навыков находить сумму n первых членов арифметической прогрессии, применяя формулы; контроль ранее изученного;
- развитие умений учебного труда, внимания, речи, слушать, участвовать в коллективном обсуждении проблемы;
- воспитание активности, самостоятельности, ответственности, умения доводить начатое дело до конца.
Оборудование: карточка-тест, учебник
Тип урока: комбинированный
Технологии: проблемное обучение, тестовая, дифференцированное обучение.
Формы работы учащихся: самостоятельная, фронтальная
Прогнозируемый результат: в результате изучения материала учащиеся смогут применить полученные знания для решения стандартных задач по данной теме.
Структура урока:
-
Организационный момент.
-
Актуализация ранее изученного и постановка цели урока.
-
Изучение нового материала.
-
Формирование умений.
а) работа по учебнику
б) самостоятельная работа - тест
-
Итог урока, сообщение домашнего задания
ХОД УРОКА
I Организационный момент.
Проверка готовности класса к уроку.
II. Актуализация ранее изученного и постановка цели урока.
Учитель.
На предыдущих уроках мы с вами познакомились с различными последовательностями и способами их задания. Среди всего разнообразия мы особо выделили одну, называемую «Арифметической прогрессией». Вспомним, что мы знаем о ней.
-2-
Математический диктант
Цель: контроль и коррекция ранее изученного, проверка осознанного выполнения домашнего задания, введение в новую тему.
-
Какая из последовательностей заданных формулой n-го члена, является арифметической прогрессией?
а)
хn=
2n
+5 б) хn
= 3n(n
+ 2); в) хn
=
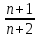
-
Дана арифметическая прогрессия (сn): с1; с2; с3; 29; 32; с6; ….
Найдите: а) d;
б) с3;
в) с6;
г) с1;
д) с2;
е) найдите сумму шести первых членов арифметической прогрессии.
ж) найдите сумму 30-первых членов арифметической прогрессии.
(Здесь возникает вопрос: неудобно, громоздко)
Проблема: Нельзя ли решить эту задачу проще? Можно! Но для этого нужно познакомиться с формулой суммы n первых членов арифметической прогрессии.
Учитель Итак, тема урока «Формула суммы n первых членов арифметической прогрессии». Сформулируйте цели урока.
III. Изучение нового материала.
Учитель.
С формулой суммы n первых членов арифметической прогрессии связан эпизод из жизни немецкого ученого Карла Гаусса (показать портрет). Когда ему было 9 лет, учитель, занятый проверкой работ других классов, задал на уроке следующую задачу:
«Сосчитать сумму натуральных чисел от 1 до 100 включительно». Каково же было его удивление, когда один из учеников (это был Гаусс) через минуту воскликнул: «Я уже решил». Большинство учеников после долгих подсчетов получили неверный результат. В тетради Гаусса было написано только одно число, и притом верное.
Со схемой его решения вас познакомит…. (ФИ ученика хорошо успевающего, с ним заранее был рассмотрен данный вопрос).
Учитель
Используя
эти рассуждения найдем сумму n-первых
членов арифметической прогрессии.
(Вывод формулы Sn
=
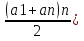 .
.
-3-
Учитель.
Есть еще одна формула суммы n-первых членов арифметической прогрессии.
Sn=
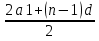 ∙n
∙n
Как получить эту формулу из первой? (Выслушать предложения)
- Что должны знать, чтобы применить первую формулу? А вторую? А знаем формулу n-го члена арифметической прогрессии? Какие будут предложения? (Идет вывод второй формулы).
Примеры
-
Из диктанта вернемся к заданию №2 (е,ж). Найдите применяя формулу S6 и S30. (Один ученик на доске, остальные в тетради).
-
Из диктанта №1 рассмотрим формулу (а). Найдите S40.
IV.Формирование умений.
а) Работа по учебнику: № 603 (б); №604 (а); №606 (а);
б) Тест
Цель: в процессе самостоятельной деятельности учащихся довести до их сознания содержание формулы суммы n-первых членов арифметической прогрессии; проверить, насколько учащийся понял и научился применять новые знания.
(Каждый учащийся получает карточку-тест, после выполнения идет проверка и разбор ошибок))
Карточка-тест
1.Установите порядок действий для вывода формулы суммы Sn n-первых членов арифметической прогрессии:
Записать сумму Sn членов арифметической прогрессии от первого до
n-го, расположив слагаемые в порядке убывания их номеров под
аналогичным равенством.
Выразить сумму Sn из последнего равенства.
Обратить внимание на то, чему равна сумма каждой пары членов
прогрессии, расположенных друг под другом, и сколько таких пар.
Сложить почленно оба равенства.
Записать сумму Sn членов арифметической прогрессии от первого до
n-го, расположив слагаемые в порядке возрастания их номеров.
-4-
2. выбрать формулу суммы n-первых членов арифметической прогрессии:
а) Sn
=
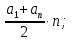 б) Sn=
б) Sn=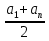 ;
в) Sn=
;
в) Sn=
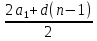 ∙n;
г) Sn
=
∙n;
г) Sn
=
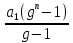
3. Найти сумму тридцати первых членов арифметической прогрессии, если а1 = 10;
а30 =25.
а) 17,5; б) 525; в) 35; г) 1050
V. Итог урока, сообщение домашнего задания.
а) Рефлексия:
-
Групповая.
Ответить на вопросы.
Как мы выполнили свою учебную задачу?
Как мы можем оценить свою работу на уроке? Почему?
С каким настроением мы заканчиваем урок?
-
Индивидуальная.
Каждый ученик получает лист и отвечает на вопросы:
Я запомнил, что……
Что было легко?
Что было трудно?
Оцените свою активность на уроке по шкале от 0-5
Что понравилось?
Что не понравилось?
Какую отметку вы себе поставили за работу?
б) Сообщение и разбор домашнего задания:
п. 26; №603(а); №606 (б); № 610 (разобрать).
в) Всех поблагодарить за работу на уроке.
-5-
Литература
-
М.Р. Леонтьева, С.Б. Суворова. Упражнения в обучении алгебре. Книга для учителя. Москва «Просвещение» 1985.
-
Ю.Н. макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под редакцией С.А. Теляковского. Алгебра. 9 класс: учебник для общеобразовательных учреждений. Москва «Просвещение», 2010.
-
И. Шальнов, С. Шальнова. Тесты к школьному учебнику: Алгебра. 9 класс: справочное пособие. Москва «АСТ-ПРЕСС» 1998.
- Международный вебинар «Волонтёрство и новые воспитательные практики в школе»
- Международный вебинар «Обучение грамоте старших дошкольников с помощью развивающих игр В. В. Воскобовича: практика реализации ФГОС и ФОП ДО»
- Вебинар «Речевое развитие детей дошкольного возраста в разных видах деятельности (ФГОС ДО)»
- Вебинар «Современные технологии речевого развития детей дошкольного возраста: синквейн, мнемотехника, ТРИЗ, РТВ»
- Международный вебинар «Современные методы нейрореабилитации и нейрокоррекции. Нейропсихологическая коррекция в системе комплексной реабилитации. Общий анализ принципов коррекционного и восстановительного обучения в нейродефектологии»
- Международный вебинар «Онтогенез и дизонтогенез в нейродефектологии»






Преимуществом работы является подробное изложение заданий к уроку, попытка использовать проблемное обучение (проблема в начале урока обозначена, но в дальнейшем нет акцента на ее разрешении).
К недостаткам можно отнести повторение цели урока и одной из задач урока, нераскрытие заявленной технологии обучения, а именно, дифференцированное обучение никак не проявляется в конспекте. Кроме этого, присутствуют опечатки и неточности.
Автор разместил свою работу на двух педагогических сайтах, в этом не было необходимости.
Конспект нельзя использовать как методический документ, но можно как источник заданий к уроку.
Согласно требованиям портала на титульной странице должен быть логотип портала (раздел Справка Главного меню).