Контекстное обучение как средство формирования математической компетентности учащихся
Описание опыта работы Тема: «Контекстное обучение как средство формирования математической компетентности учащихся»
Выполнила: Купш Ольга Николаевна учитель математики
Литковка-2012 ОГЛАВЛЕНИЕ
|
| Введение
| 3
|
| Глава I
| Контекстное обучение как средство формирования математической компетентности
| 6
|
|
| 1.1 Теоретическое обоснование компетентностного подхода в образовании
| 6
|
|
| 1.2 Контекстное обучение как средство формирования математической компетентности школьников
| 7
|
| Глава II
| Внедрение контекстного обучения как средства формирования математической компетентности учащихся 5-6 классов
| 10
|
|
| 2.1 Приемы и методы контекстного обучения математике
| 10
|
|
| 2.2 Методика изучения нового материала в рамках контекстного обучения
| 10
|
|
| 2.3 Проектная деятельность учащихся как средство контекстного обучения математике в 5-6 классах
| 13
|
|
| 2.4 Методические рекомендации для работы над контекстными заданиями по математике для 5-6 классов.
| 14
|
|
| Заключение
| 19
|
|
| Список литературы и интернет источников
| 22
|
|
| Приложения
| 23
|
|
| 1. Методическая разработка урока математики в 6 классе по теме «Умножение обыкновенных дробей»
|
|
|
| 2. Информационная карта ученического проекта «Живой градусник»
|
|
|
| 3. Контекстные задания по математике для 5-6 классов и инструментарий отслеживания уровня сформированности математической компетентности по теме «Обыкновенные дроби»
|
|
ВВЕДЕНИЕ
Российское общество сегодня переживает период глубоких структурных, в том числе социокультурных изменений. Этот процесс не может не затрагивать сферу образования и воспитания.
Главная задача российской образовательной политики – обеспечение современного качества образования на основе сохранения его фундаментальности и соответствия актуальным и перспективным потребностям личности, общества и государства. Основные принципы образовательной политики в России определены в Законе Российской Федерации «Об образовании», а также в Федеральной программе развития образования.
Основываясь на документах «Стратегии модернизации содержания образования» [8], «Концепции модернизации российского образования на период до 2010 года» [4], можно отметить, что происходит резкая переориентация оценки результата образования с понятий «подготовленность», «образованность», «общая культура», «воспитанность», на понятия «компетенция», «компетентность обучающихся», «способность к адаптации в новых условиях». Современный уровень отношений в обществе характеризуется возрастанием требований к уровню развития личности.
В национальной образовательной инициативе «Наша новая школа» также подчеркнуто, что требования к результатам должны включать не только знания, но и умения их применять. В число таких требований должны войти компетентности, связанные с идеей опережающего развития, все то, что понадобится школьникам и в дальнейшем образовании, и в будущей взрослой жизни.
Модернизация школьного образования ориентирует на развитие познавательной самостоятельности учащихся, формирование у них умений исследовательской деятельности. Одна из задач сегодня – формирование молодого человека с критическим, нестандартным мышлением, способного к поиску взвешенных решений, основанных на самостоятельном исследовании окружающего мира. Такие люди будут определять успехи нашей страны в будущем.
Таким образом, компетентностный подход (В.А.Болотов, А.В. Вишнякова, С.Г. Воровщиков, И.А.Зимняя, А.В. Хуторской, И.С. Якиманская, А.Л Андреев,А.Дахин, Г.К. Селевко и др.) ложится в основу обучения в общеобразовательной школе.
По результатам международного тестирования PISA-2006, ориентированного на проверку сформированности компетентностей в различных циклах (естественнонаучный, математический, гуманитарный), Россия набрала балл ниже среднего по уровню сформированности математической компетентности. При этом результаты учащихся начальной школы достаточно высоки, что говорит о низком уровне преемственности при переходе с первой ступени обучения на вторую.
Исходя из выше сказанного, находим противоречие между необходимостью формирования математической компетентности учащихся и недостаточно разработанной системой приемов, методов и форм реализации данного направления на средней ступени обучения.
Моя работа «Контекстное обучение как средство формирования математической компетентности учащихся 5-6 классов» посвящена разрешению данного противоречия.
Цель работы: обобщение системы работы по внедрению контекстного обучения как средства формирования математической компетентности учащихся 5-6 классов.
Для достижения поставленной цели и решения проблемы выделены следующие задачи:
1. Провести анализ теоретического состояния и практического опыта по вопросам формирования математической компетентности школьников.
2. Осуществить внедрение контекстного обучения как средства формирования математической компетентности учащихся 5-6 классов в учебный процесс.
3. Разработать и обосновать систему контекстных заданий, направленную на формирование математической компетентности учащихся 5-6 классов.
4. Разработать инструментарий по оценке уровня сформированности математической компетентности учащихся 5-6 классов.
5. Провести опытно-экспериментальное исследование, направленное на проверку влияния методики контекстного обучения на формирование математической компетентности учащихся 5-6 классов.
Объектом исследованиявыступает процесс обучения математике в 5-6 классах общеобразовательной школы в рамках компетентностного подхода.
Предмет исследования: технология контекстного обучения как средство формирования математической компетентности учащихся 5-6 классов.
Контекстное обучение разрабатывается более 25 лет А.А. Вербицким, однако, лишь для высшего образования. В средней школе методические разработки внедрения технологии контекстного обучения недостаточны для полной реализации, что обуславливает актуальность моей темы, её практическую значимость и новизну.
ГЛАВАI.КОНТЕКСТНОЕ ОБУЧЕНИЕ КАК СРЕДСТВО ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКОЙ КОМПЕТЕНТНОСТИ ШКОЛЬНИКОВ
1.1 Теоретическое обоснование компетентностного подхода в образовании
По мнению А.Л.Андреева: «В некотором смысле компетентностная парадигма как бы представляет в сфере образования то, что называют современностью, и в этом смысле она противопоставляется несовременному, архаическому, отжившему. Исторические рубежи современности при этом компетентностная модель образованности соотносится с динамичным «открытым» обществом, в котором продуктом процессов социализации, обучения, общей и профессиональной подготовки к выполнению всего спектра жизненных функций должен стать ответственный индивид, готовый к осуществлению свободного гуманистически ориентированного выбора.» [1, C.2]
Что же понимают под компетентностью? Компетентность-это способность решать возникающие в различных сферах жизни конкретные проблемы. Такой подход предполагает наличие знаний, способностей обладать определенными личностными качествами и уметь в любой момент найти и отобрать нужные знания для решения проблемы.
Компетентностный подход – это деятельностный подход. «Под компетентностью чаще понимается интегральное качество личности, проявляющееся в общей способности и готовности её деятельности, основанной на знаниях и опыте, которые приобретены в процессе обучения и социализации и ориентированы на самостоятельное и успешное участие в деятельности» [7, C.8].
Традиционные методы обучения направлены, в основном, на усвоение учащимися большого объема знаний, полученных в готовом виде от учителя. Умения при такой методике отрабатываются, по принципу «Делай как я», то есть по образцу, предложенному учителем, а навыки формируются в результате решения большого количества аналогичных задач, что исключает самостоятельную работу учащихся с первоисточниками и дополнительной литературой. В результате недостаточно развиваются творческое отношение к делу и самостоятельность при решении задач. Тенденция гуманизации образования требует поставить в центр процесса обучения личность ученика. Современному учителю, необходимо использовать методики обучения, направленные на персонифицированную личность объекта обучения. Таким образом, на современном этапе развития школьного образования одним из основных направлений является решение проблемы разработки эффективных методов преподавания и обеспечение качественного усвоения знаний учащимися.
1.2 Контекстное обучение как средство формирования математической компетентности учащихся
Социологи и ученые педагоги признают, что ценности сегодня сменились: и на коне не тот, кто много знает, а тот, кто умеет этими знаниями с толком распоряжаться и поэтому наша задача, задача педагогов не только научить детей, но и уметь применить свои знания в современной жизни.
Моя работа направлена на формирование математической компетентности учащихся на уроках математики в 5-6 классов.
Понятие математической компетентности отображено в различных источниках.
По мнению Г.Селевко: «математическаякомпетентность – это умение работать с числом, числовой информацией (владеть математическими умениями)» [7, C. 139].
По мнению ученых — исследователей, разработавших материалы по оценке знаний и умений для международной программы РISA, «математическая компетентность — это наиболее общие способности и умения, включающие математическое мышление, письменную и устную математическую аргументацию, постановку и решение проблемы, математическое моделирование, использование математического языка, современных технических средств» [5, C. 132].
Таким образом, становится ясным тот факт, что математическая компетентность — это владения математическим умениями. Можно утверждать, что математическая компетентность — это в совокупности математические знания, умения, навыки + опыт практической деятельности, умение применять «зун» на практике, в окружающей действительности.
В исследовании PISAвыделяются три уровня математической компетентности: уровень воспроизведения, уровень установления связей, уровень рассуждений.
Формирование математической компетентности на уроках предполагает обучение с использованием приемов, направленных на необходимость использования внешних и внутренних знаний, умений учащихся, включения в активную деятельность по решению той или иной проблемной ситуации, решению контекстных заданий. Реализация этого возможно при осуществлении контекстного обучения в учебном процессе.
Что же подразумевает собой контекстное обучение?
По мнению А.Вербицкого: «контекстное обучение выступает концептуальной основой реализации компетентностного подхода в образовании».
Контекстное обучение предполагает максимально широкое введение в учебный процесс видов, форм и методов деятельности, позволяющих перейти от преимущественно информационных форм к активным методам и формам обучения с включением элементов проблемности, научного поиска, широкого использования резервов самостоятельной работы обучающихся [3, С. 41].
В центре теории контекстного обучения находится понятие контекста.
Контекст– это система внутренних и внешних условий жизни и деятельности человека, которая влияет на восприятие, понимание и преобразование им конкретной ситуации, придавая смысл и значение этой ситуации как целому, так и ее компонентам. Внутренний контекст представляет собой индивидуально-психологические особенности, знания и опыт человека. Внешний контекст – предметные, социокультурные, пространственно-временные и иные характеристики ситуации, в которых он действует [3, С. 41].
В качестве основных принципов контекстного обучения были выбраны следующие: определение обучающегося как активного субъекта познания; его ориентация на самообразование и саморазвитие; опора на субъективный опыт учащегося; индивидуальная направленность образовании.
Анализируя данные анализа действующих учебников по математике можно сделать вывод о необходимости создания дидактических материалов для качественного осуществления контекстного обучения математике в 5-6 классах.
Для разрешения этой проблемы и реализации контекстного обучения на уроках математики мной разработаны следующие материалы для 5-6 класса: контекстные задания, фрагменты уроков с применением ИКТ, темы и содержание ученических проектов для 5-6, контрольные работы для отслеживания уровня сформированности математической компетентности. Подтверждение результативности отражены в результатах мониторинга.
ГЛАВА II. ВНЕДРЕНИЕ КОНТЕКСТНОГО ОБУЧЕНИЯ КАК СРЕДСТВА ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКОЙ КОМПЕТЕНТНОСТИ УЧАЩИХСЯ 5-6 КЛАССОВ В УЧЕБНЫЙ ПРОЦЕСС
2.1 Приемы и методы контекстного обучения математике
Для реализации контекстного обучения математике необходимо проводить внедрение основных приемов, методов, принципов контекстного обучения во все направления учебного процесса. На уроках осуществление контекстного обучения возможно на всех этапах урока: от подготовительного до изучения нового материала и его закрепления. Во внеурочной деятельности реализация элементов контекстного обучения возможно при осуществлении проектной деятельности учащихся. Таким образом, на уроках математики я применяю различные методы и приемы для развития творческих способностей и сформирования математической компетентности учащихся. В своей работе я использую: Методы: проектный, проблемный, поисковый, развивающий, исследовательский. Приемы: ролевая игра, творческая проектная деятельность, создание проблемной ситуации, выполнение развивающих заданий, воображаемое путешествие, реферат, опережающее задание, использование мультимедийных средств обучения.
2.2 Методика изучения нового материала в рамках контекстного обучения
Проиллюстрируем осуществление реализации контекстного обучения в математике на примере изучения нового материала в 6 классе по теме «Центральная симметрия» на подготовительном этапе, этапах изучения нового материала и закрепления.
1)Подготовительный этап
На предыдущем уроке математике детям предлагается домашнее задание под названием «Праздничный стол», следующего содержания: вместе с родителями «накрыть» праздничный стол, оформив на альбомном листе схему расстановки одного горячего блюда, четырех салатов. Сделать это нужно красиво, эстетично. Можно принести свои рецепты данных блюд. В зависимости от внутренних условий каждый предлагает свой способ оформления.
2) Этап изучения нового материала
Изучение нового материала осуществляется последовательно:
· Рассматриваются различные модели оформления праздничного стола, выделив те рисунки, на которых расстановка выполнена по правилам центральной симметрии. Например: Г- горячее блюдо, С – салат и т.д. (рис. 1)
Рис. 1 · Выделяются общие свойства рисунков, выполненных по правилам центральной симметрии, отмечается гармоничное расположение и эстетичность оформления. Тем самым детьми выделяются свойства центрально-симметричных фигур.
· По схеме «ученик — учитель — ученик» формулируется определение центрально-симметричных фигур. Строится математическая модель (две центрально-симметричные точки).
· Предлагается выбрать из предложенных рисунков те, на которых используется центральная симметрия (рис. 2).
3) Задания на закрепление изученного материала
Мы соглашаемся с уровнями математической компетентности, предложенные в исследовании PISAи сформулированные выше. В соответствии с ними составлены следующие задания для успешного закрепления нового материала.
Задание 1 уровня.Приведите примеры геометрических фигур, имеющих центр симметрии (возможные варианты примеров: квадрат, ромб и другие).
Задание 2 уровня. Начертите треугольник АВС, отметьте точку О и постройте треугольник, симметричный треугольнику АВС относительно этой точки, если: а) точка О – вне треугольника; б) точка О – внутри треугольника; в) точка О – середина стороны АВ; г) точка О – совпадает с вершиной А.
Задание 3 уровня.Нарисовать в тетради 3 примера орнамента с элементами центральной симметрии: 1) орнамент, связанный с национально-региональным компонентом (ханты-мансийский орнамент); 2) национальный; 3) придумать свой. Показать центральную симметрию на одном из фрагментов (умеющим работать с компьютером, дается возможность сделать его в электронном виде дома).
Таким образом, на каждом этапе, начиная от домашнего задания, являющегося подготовительным этапом, до изучения нового материала и этапа его закрепления, учащиеся принимают активное участие в учебном процессе. Ребенок для выполнения заданий привлекает все имеющиеся в его распоряжении знания, способы действия, актуализация которых позволяет производить анализ введенных понятий. Вместе с тем в контексте проблемы выявляются новые связи и отношения между элементами, такие условия проблемы, которые не были заданы, благодаря чему происходит расширение поиска возможных средств решения, достижения поставленной цели. Реализация найденных закономерностей в итоге сводится в одних случаях к выполнению операций, связанных с практической деятельностью по изготовлению создаваемой конструкции, в других — к выполнению вычислений, в третьих – к построению системы доказательств, обосновывающих достигнутое решение [15, С. 193].
2.3 Проектная деятельность учащихся как средство контекстного обучения математики в 5-6 классах
Одним из методов реализации контекстного обучения математике является метод проектов. Понятие проекта достаточно широко введено в литературе, потому рассмотрим лишь его определение и место в учебном процессе, организованном по принципам контекстного обучения.
Проект – (от лат. projectus, в буквальном переводе – брошенный вперед), 1) реалистичный замысел, план о желаемом будущем; 2) совокупность документов (расчетов, чертежей, макетов) для создания какого-либо продукта, содержит в себе рациональное обоснование и конкретный способ осуществления; 3) метод обучения, основанный на постановке социально-значимой цели и её практическом применении.
Мной разработана система ученических проектов, которые выполняются к темам изучаемого материала и направлены на достижения следующей цели: способствовать развитию творческих способностей, умений добывать необходимую информацию, самостоятельно анализировать её и представлять в виде единого целого продукта; развитию интереса к математике, привитию ученикам математической культуры и расширению кругозора учащихся. В содержание проектов входят задания опережающего характера.
Организация проектной деятельности предполагает разбиение класса на творческие группы по 4-5 человек, которые совместно осуществляют выполнение поставленного перед ними задания.
Тематика проектов для 5,6 класса:
· Проект «Обыкновенные дроби. Исторический экскурс»
· Проект «Сказка «В царстве геометрических фигур»
· Проект «Проценты. Исторический экскурс»
· Проект «Родная школа помещается в ладони» (создание макета здания школы), тема «Масштаб», «Прямоугольный параллелепипед»
· Проект «Положительные и отрицательные числа вокруг нас», «Положительные и отрицательные числа. Исторический экскурс»
· Проект «Живой градусник»
· Проект «Параллельные прямые»
· Проект «Координаты. Откуда? Где? Зачем? „
· Проект “Её величество — Пропорция»
Задание для выполнения проекта творческой группе учащихся с указанием основных требований, критериев оценивания выдается в виде информационной карты. Пример информационной карты представлен в приложении.
2.4 Методические рекомендации для работы над контекстными заданиями по математике для 5-6 классов
В рамках исследования мной разработаны контекстные задания по математике для 5-6 классов по темам «Обыкновенные дроби», «Десятичные дроби», «Положительные и отрицательные числа».
В процессе изучения математики огромную роль играет решение задач. Дело не только в применении полученных знаний на практике. По мнению ведущих методистов, без решения задач невозможно овладеть теорией, так как процесс решения задачи позволяет раскрыть взаимосвязь основных математических понятий и свойств между собой, а также окружающей нас действительностью.
Правильная постановка и подбор тематики задач и упражнений в обучении математике во многом определяет современную методику преподавания. Процесс решения задачи может служить различным целям обучения, задачи могут быть использованы при изучении новой темы, для самостоятельного установления учащимися какого-либо математического факта.
Задачи могут быть предложены учащимся с целью глубокого усвоения теоретического материала или выработки необходимых умений и навыков. Например, при изучении темы: «Десятичные дроби» можно предложить учащимся следующую задачу:
«В бочке <metricconverter productid=«180 литров» w:st=«on»>180 литров бензина. В первый день было израсходовано 0,6 этого количества. Сколько литров бензина осталось в бочке?»
Рассмотрим возможный сценарий фрагмента учебного занятия:
10.Для выполнения данного задания нужно взять учебник по географии или энциклопедию. Возможный вариант:
«Стада антилопы гну способны проходить огромные расстояния в поисках воды и пищи. Одно такое стадо прошло в течение нескольких дней путь в 200километров. В первый день им было пройдено 0,6 пути. Сколько километров осталось пройти антилопам туда, где идет дождь и много растительности?»
| Деятельность учителя
| Деятельность учащихся
|
| 1. Изучите содержание задачи
2.Определите, исходя из данной ситуации тип задачи. 3.Составьте краткую запись 4.Сформулируйте правило 5.Каков план решения задачи? 6.Запишите решение данной задачи 7. Существуют ли другие способы решения данной задачи? 8. Измените вопрос в задаче так, чтобы она решалась в одно действие 9. Измените условие задачи так, чтобы она решалась в одно действие 10.В качестве домашнего задания: Составьте аналогичную по способу решения задачу по теме: «Животный мир Африки». | 1.Повторно читают задачу.
2. Задача на нахождение дроби от числа. 3. Составляют краткую запись. 4.Проговаривают правило нахождения дроби от числа 5.В начале, применяя правило, найдем количество израсходованного бензина, а затем вычтем полученный результат из 180. 6.1) 180*0,6=108(л) израсходовали 2)180-108=72(л) осталось. 7.Другой способ: Все количество бензина примем за 1. Тогда решение будет таким: 1)1-0,6=0,4 (ч) бензина осталась 2) 180*0,4=72(л) бензина осталось. Ответ: 72 литра. 8.Сколько литров бензина было израсходовано в первый день? 9.В бочке было <metricconverter productid=«180 литров» w:st=«on»>180 литров бензина. После того, как в первый день израсходовали часть бензина, в бочке осталось 0,6 от первоначального количества. |
Задачи могут использоваться при обучении учащихся деятельности поисковой и творческой. Это способствует развитию у учащихся математического мышления. Например, при изучении темы «Среднее арифметическое» можно предложить такую задачу: «В семье работают отец, сын и дочь. Отец заработал за месяц 40 тысяч рублей, сын -20 тысяч рублей, а дочь-15 тысяч рублей. Каков средний заработок среднего члена семьи?»
В качестве домашнего задания можно предложить следующее:
Выясните, сколько денег заработали за прошлый месяц члены вашей семьи. Используя полученные данные, составьте и решите задачу, аналогичную исходной.
Разработанные задания представлены дифференцированно. Для удобства работы все составленные задания разделены по темам: «Действия с обыкновенными дробями», «Действия с десятичными дробями», «Действия с положительными и отрицательными числами».
Также разработан инструментарий, позволяющий учителю определить уровень сформированности у учащихся математической компетентности.
Возможно, такой подход в обучении позволит снять назревшее противоречие между необходимостью формирования у учащихся математической компетентности и реально сложившейся практикой обучения, позволит сформировать устойчивый интерес к предмету.
ЗАКЛЮЧЕНИЕ
Результаты эксперимента по внедрению контекстного обучения в учебный процесс за 2011-2012 учебный год позволяют сделать следующие выводы:
— благодаря использованию технологии контекстного обучения соблюдена преемственность при переходе учащихся на следующую ступень обучения, что подтверждается результатами успеваемости учащихся;
— организация учебного процесса на основе контекстного обучения математике позволяет повысить уровень математической компетентности учащихся 5-6 классов.
— внедрение контекстного обучения способствовало повышению познавательного интереса к предмету, что подтверждается результатами анкетирования учащихся.
Мониторинг успеваемости экспериментальной группы учащихся Анкетирование в контрольной и экспериментальной группах «Познавательный интерес к предмету «математики»
| Вопросы | да | нет |
| 1. Нравиться ли тебе преподавание математики?
| 92% | 8% |
| 2. Пригодятся ли тебе в будущем знания, полученные на уроках математики?
| 88% | 12% |
СПИСОК ЛИТЕРАТУРЫ 1. Андреев А. Л.Компетентностная парадигма в образовании: опыт философско-методологического анализа // Педагогика. — 2005. — № 4. – С. 19-27.
2. Вербицкий А. Гуманизация, компетентность, контекст – поиски оснований интеграции // «Alma mater» (Вестник высшей школы). – 2006. № 5. – С. 19-25.
3. Вербицкий А. Контекстное обучение в компетентностном подходе // Высшее образование в России. – 2006. № 11. – С. 39-46.
4. Концепция модернизации российского образования на период до 2010 года. – М., 2002
5. Краснянская К.А. Оценка математической грамотности 15-летних учащихся (PISA-2006) // Школьные технологии. – 2008. № 3. – С. 161-171.
6. Ларионова О.Г. Интеграция личностно-центрированного и компетентностного подходов в контекстном обучении (на материале подготовки учителя математики). – Автореферат на соискание ученой степени доктора педагогических наук, Москва 2007
7. Селевко Г. Компетентности и их классификация \\ Народное образование. – 2004. — № 4. – С. 138-142.
8. Стратегия модернизации общего образования. Материалы для разработки документов по обновлению общего образования. — М., 2001. С.34
9. Шквыря Е.Л. Конструирование математических задач: Учебное пособие / сост. Е.Л.Шквыря. Нижневартовск: НГГУ, 2007. – 27 с.
ИНТЕРНЕТ – ИСТОЧНИКИ 1.http://www.edu.ru– Министерство образования РФ
2. http://sc.nios.ru/about/ — коллекция цифровых образовательных ресурсов для учреждений общего и начального профессионального образования.
ПРИЛОЖЕНИЯ
| Приложение 1 Методическая разработка урока математики в 6 классе по теме «Умножение обыкновенных дробей» |
| |
| Предмет:
| математика
| |
| Класс:
| 6
| |
| Тема:
| Умножение обыкновенных дробей
| |
| Тип:
| Урок изучения нового материала
| |
| Цели:
| — повторить основные действия с обыкновенными дробями, вывести правило умножения обыкновенных дробей, закрепить при выполнении заданий, проверить уровень усвоения материала;
— способствовать развитию логического, аналитического, критического мышления; интереса к математике; — способствовать воспитанию умений работать в парах, самостоятельно, коллективно; — способствовать формированию математической компетентности учащихся. | |
| Методы:
| проблемно-поисковый, исследовательский
| |
| Оборудование:
| ПК, интерактивная доска, карточки для игры «Лото», карточки для самостоятельной работы по новой теме, мел, доска.
| |
| Формы работы:
| самостоятельная, работа в парах, фронтальная работа.
| |
| План урока:
| 1. Организационный момент (2 мин.)
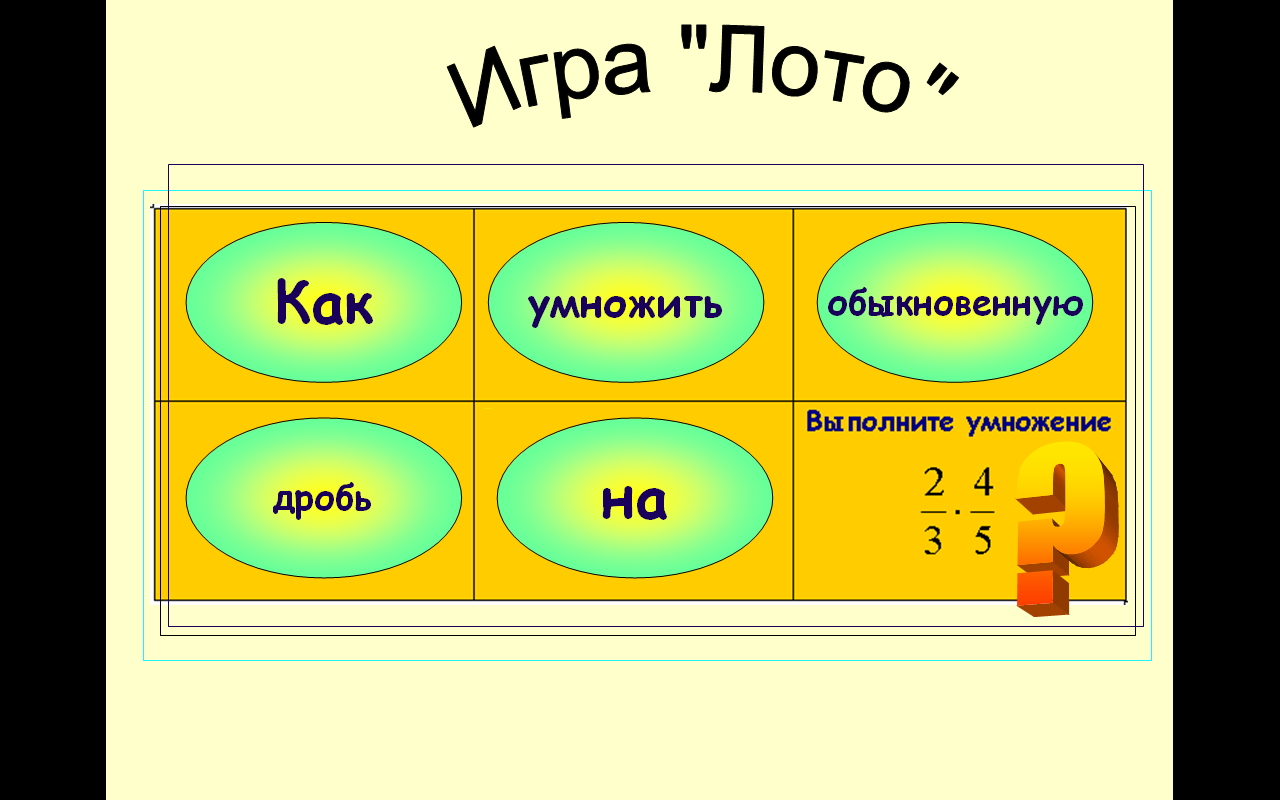
2. Актуализация знаний – игра «Лото» (6 мин.) 3. Изучение нового материала (5 мин.) 4. Закрепление изученного материала (7 мин.) 5. Проверочная работа (8 мин.) 6. Решение практической задачи (7 мин.) 7. Рефлексия урока (2 мин.) 8. Домашнее задание (3 мин.) | |
| Деятельность учителя | Деятельность учащихся | Оформление доски |
| 1. Организационный момент | ||
| Здравствуйте, дорогие ребята! Садитесь!
(приветствие) Я рада приветствовать Вас на уроке математики и прошу обратить внимание на доску. Прочитай, Полина, что написано. Как Вы понимаете это высказывание? Абсолютно точно! Это высказывание будет девизом нашего сегодняшнего урока! Мы будем мыслить, рассуждать, исследовать и только так получать знания по математике! А какую тему мы сейчас изучаем, какую область математики мы «осиливаем» сейчас? Что из этого раздела мы уже знаем и умеем? Чтобы продуктивно работать на уроке нам нужно достать из наших сундучков знания, которые мы уже имеем предлагаю Вам игру «Лото». | (присаживаются)
Дорогу осилит идущий, а математику мыслящий! (пример ответа ученика) Я понимаю это так: если человек знает куда идти, то он осилит дорогу, также и в математике, если ты мыслишь, то встречаясь с проблемой, всегда сможешь найти способ её решения! Мы изучаем тему «Обыкновенные дроби». Мы умеем складывать дроби с одинаковыми, разными знаменателями, умножать и делить на натуральное число. |
|
Необходимо выполнить задания на листе, полученный результат найти на соответствующей карточке и приложить её обратной стороной к заданию. В результате получится шифр. Если какое-то задание Вы выполнить не можете, положите на него знак «?».
(Контролирует выполнение заданий)
(Фронтальная работа, вместе с учащимися заполняют табло на доске, анализируют шифр)
(Подводит учащихся к формулировке проблемного вопроса – как умножить обыкновенную дробь на дробь)
Что ж, сегодня наши мыслительные операции будут направлены на то, чтобы найти ответ на это проблемный вопрос, этому и посвятим наш урок. Итак, тема нашего урока «Умножение обыкновенных дробей».
Курс задан, какова цель урока?
(Внимательно слушают, задают вопросы, если они есть).
(Выполняют задания, пара, заполнившая карточку «Лото» поднимает руку, после того как большинство выполнили задание – фронтальная проверка)
(В результате работы приходят к проблемному вопросу – как умножить обыкновенную дробь на дробь, так как решить последний пример им не удалось, в силу того, что задание новой не изученной темы)
(формулируют с учителем тему урока, записывают её в тетрадь)
Научиться умножать обыкновенные дроби, вывести правило умножения обыкновенных дробей.
3. Изучение нового материала (фронтальная работа) Для достижения цели и получения ответа на проблемный вопрос предлагаю Вам выполнить небольшое исследование.
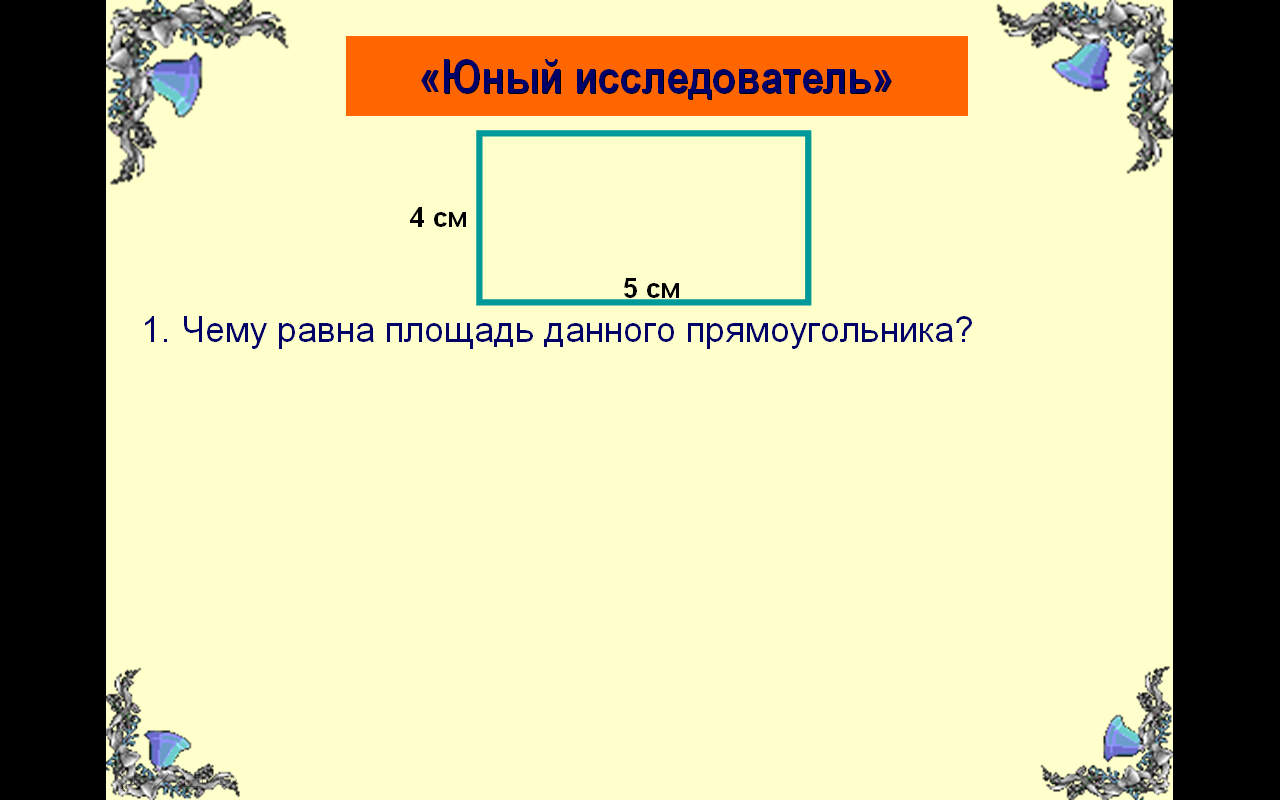
Обратите внимание на доску. Охарактеризуйте условие и данные.
Как найти площадь данного прямоугольника?
Что произойдет с площадью прямоугольника, если длину и ширину одновременно уменьшить в 10 раз?
Как это можно записать в виде равенства с обыкновенными дробями?
Но ребята, посмотрите внимательно, что у нас получилось – сами того не предполагая мы выполнили умножение обыкновенных дробей! Проанализируйте равенство, выделите закономерности- как же выполнить умножение обыкновенных дробей.
(по схеме: УЧЕНИК-УЧИТЕЛЬ-УЧЕНИК формулируется правило)
Молодцы!!! Вот и наше открытие!
Запишем правило в тетради в буквенной форме.
Дан прямоугольник со сторонами 4см и 5 см. Нужно найти площадь прямоугольника.
Нужно длину умножить на ширину и получится 20 квадратных сантиметров.
(Выслушиваются ответы)
Площадь уменьшится в 100 раз.
(внимательно изучают, предлагают свои варианты ответов)
Нужно числители перемножить и знаменатели перемножить!
(по схеме: УЧЕНИК-УЧИТЕЛЬ-УЧЕНИК формулируется правило)
Чтобы умножить обыкновенные дроби нужно числители перемножить и результат записать в числитель, знаменатели перемножить и результат записать в знаменатель)
(записывают)
4*5=20 см2
4. Закрепление (самостоятельная работа) Для закрепления правила, нужно…
(2 ученика вызываются к доске, выполняют задания)
решить примеры!
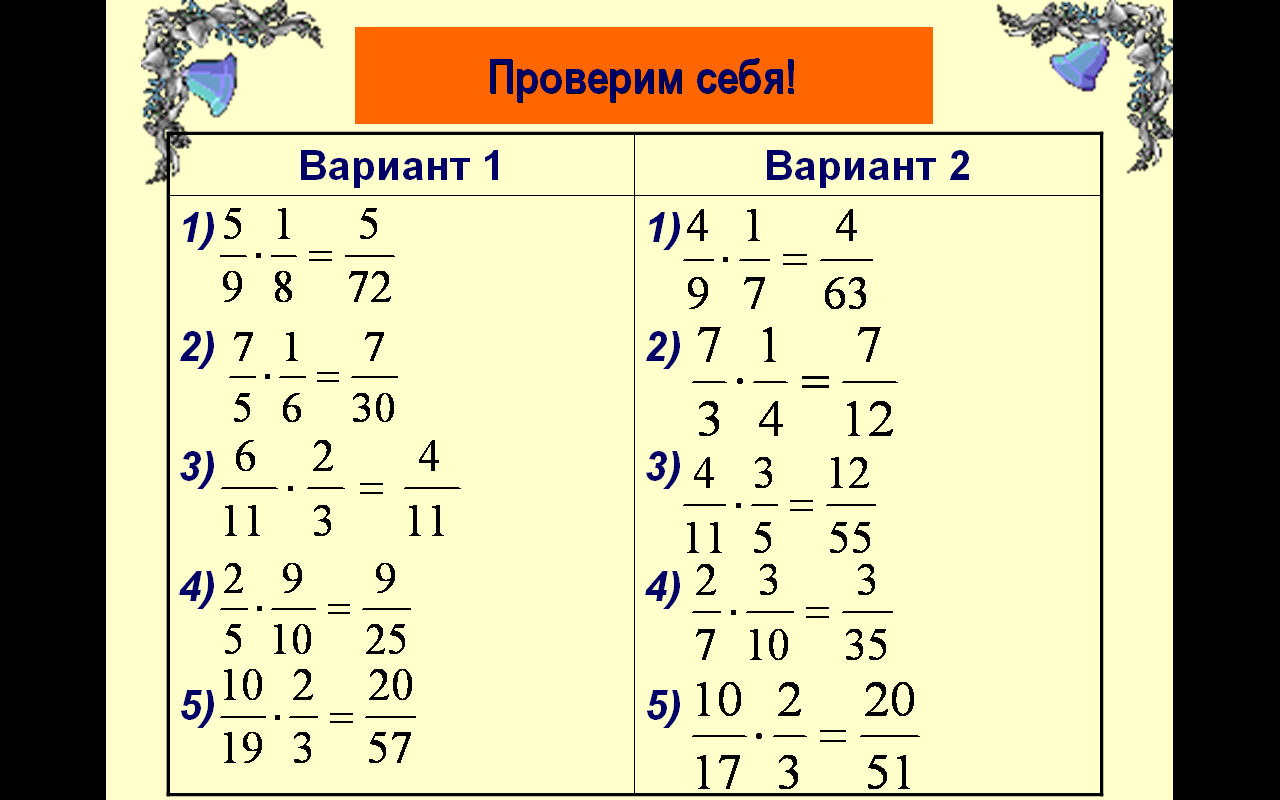
(все решают самостоятельно, затем проводят проверку решений на доске)
А теперь, ребята, я предлагаю Вам стать настоящими экспертами! Наш любимый стеснительный друг Петя Васечкин уже прорешал задания и доверил Вам проверку! Найдите ошибку в данных заданиях.
(анализируют, находят ошибки и их характер)
После определения ошибки, она выделяется анимацией на доске.
5. Проверочная работа (самостоятельная работа, взаимопроверка) (Раздаются карточки с заданиями, время работы 5 минут, затем взаимопроверка).
(Проводится анализ: количество выполнивших на «5», «4», характер ошибок)
(Решают задания на карточке, подписывают их, затем обмениваются с соседом по парте и выполняют с помощью доски взаимопроверку).
(Проводится анализ: количество выполнивших на «5», «4», характер ошибок)
6. Решение практической задачи (работа в парах) (Предлагается на закрепление решить следующую задачу)
(самостоятельно измеряют длину и ширину поверхности парты, выполняют действия, решают, записывают одно решение на доске)
7. Рефлексия урока Какова была цель урока?
Достигли ли мы цели урока?
Сформулируйте правило умножения обыкновенных дробей. Решена ли проблема, поставленная в начале урока? Какие трудности возникли? Соответствовал ли наш эпиграф уроку? Вопросы?
(Отвечают на поставленные вопросы, анализируя собственную деятельность на уроке)
8. Домашнее задание Записываем домашнее задание.
есть ли вопросы?
(контролирует запись д.з. в дневник)
(записывают, задают вопросы при возникновении таковых)
Приложение2 Информационная карта проекта «Живой градусник»
| Авторы Проекта
| учащиеся _____ класса
__________________________ ____________________________ __________________________ ____________________________ __________________________ ____________________________ |
| Срок сдачи Проекта
|
|
| Задание:
1) Изучите интересные факты о градусниках (виды, история возникновния). 2) Составьте несколько заданий, которые можно решить, используя математическую модель градусника. 3) Сделайте из ватмана «живой градусник» (размер 30см на 50см) 4) Составьте викторину по найденному материалу (минимум 7 вопросов). 5) Шаги 1, 2, 4 отобразите в презентации. | |
| План работы над Проектом
|
|
| Содержание Проекта | Презентация Проекта | Викторина | Защита Проекта | Общая отметка (ср.ариф) | |
| Критерии | — раскрытие темы;
— указание литературы, других источников. | — наглядность;
— красочность. — наличие рисунков, таблиц, схем; — возможно музыкальное сопровождение. | — содержание вопросов;
— представление вопросов; — ответы опрашиваемых. | — грамотность;
— логичность; — участие всех в группе; — понимание темы; — буклет. |
|
| Отметка |
|
|
|
|
Приложение 3 Контекстные задания по теме «Обыкновенные дроби»
1 уровень
1. Найди площадь прямоугольника, если:
а = см. Придумай задачу, аналогичную данной.
2. Составь и реши задачи, используя термины: время, скорость, расстояние.
3. Составь и реши задачу по записи: от 200 равны у.
4.Составь и реши задачу, используя следующие данные: 3300км, ; 840км.
|
кг |
5. Составь и реши задачу по разностному () и кратному отношению (в раза). Например: В магазине было красного шёлка в раза больше, чем белого. Сколько метров белого и серого шёлка было, если красного было на метров больше, чем серого? 6. Составь и реши задачу по схеме:
2 уровень
1. Марина в магазине купила кг конфет по цене 200 рублей за <metricconverter productid=«32 кг» w:st=«on»>1 кг. Какова стоимость покупки девочки? Составь и реши задачу, обратную данной.
2. Составь и реши задачу, которая бы решалась с помощью выражения: (
3.Длина прямоугольного параллелепипеда равна 20см, а ширина на см больше его длины и на 3 см больше высоты. Вычислить Vпараллелепипеда. Придумай и реши задачу обратную данной.
4.Предельный возраст яблони около 120 лет, что составляет предельного возраста тополя. Определить предельный возраст тополя. Составь и реши обратную задачу на нахождение предельного возраста яблони.
5. Придумать условие задачи по уравнению: + 2х = 12 и решить ее.
6. Придумай и реши задачу по теме: «Моя школа», которая бы решалась с помощью уравнения. Сделай проверку, решив её арифметическим способом.
3 уровень
1. Придумайте игру, которая потребовала бы от её участников знания о рациональных числах и умения выполнять действия над ними.
2. Составьте рекламу (антирекламу понятия «процент»)
3. Придумайте способ, который позволил бы каждому ученику проверить свои знания накануне контрольной работы по теме «Все действия над обыкновенными дробями»
4. Составь и реши задачу, в которой бы искомым числом было бы . В решении должно быть не менее 3-х действий.
5.Составь и реши задачу по теме: «Обыкновенные дроби», на материале русских народных сказок.
6.Составь и реши задачу по теме: «Музыка».
Рассмотрим пример контрольного среза по теме «Обыкновенные дроби», позволяющий проверить уровень сформированности математической компетентности.
этого квадрата. Какая часть квадрата осталась незакрашенной?
| уровень 1
| |
| 1
| Нарисуйте квадрат. Закрасьте |
Начертите угол, градусная мера которого равна прямого угла.
уровень 2
3
Масса трех чемоданов 32 кг. Масса Настиного чемодана такая же, как и масса двух других чемоданов вместе. Какова масса чемодана Насти?
4
Билет в кино стоит 150 рублей. Все билеты на показ фильма проданы. Что еще надо знать, чтобы найти, сколько стоят проданные билеты?
уровень 3
5
На двух полках стоят книги. На верхней полке на всех книг больше, чем на нижней. Какая часть книг стоит на верхней полке, а какая – на нижней?
КАЗЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ЛИТКОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА» ТАРСКОГО МУНИЦИПАЛЬНОГО РАЙОНА ОМСКОЙ ОБЛАСТИ
Описание опыта работы
Тема: «Контекстное обучение как средство формирования математической компетентности учащихся»
Выполнила:
Купш Ольга Николаевна
учитель математики
Литковка-2012
ОГЛАВЛЕНИЕ
|
|
Введение |
3 |
|
Глава I |
Контекстное обучение как средство формирования математической компетентности |
6 |
|
|
1.1 Теоретическое обоснование компетентностного подхода в образовании |
6 |
|
|
1.2 Контекстное обучение как средство формирования математической компетентности школьников |
7 |
|
Глава II |
Внедрение контекстного обучения как средства формирования математической компетентности учащихся 5-6 классов |
10 |
|
|
2.1 Приемы и методы контекстного обучения математике |
10 |
|
|
2.2 Методика изучения нового материала в рамках контекстного обучения |
10 |
|
|
2.3 Проектная деятельность учащихся как средство контекстного обучения математике в 5-6 классах |
13 |
|
|
2.4 Методические рекомендации для работы над контекстными заданиями по математике для 5-6 классов. |
14 |
|
|
Заключение |
19 |
|
|
Список литературы и интернет источников |
22 |
|
|
Приложения |
23 |
|
|
1. Методическая разработка урока математики в 6 классе по теме «Умножение обыкновенных дробей» |
|
|
|
2. Информационная карта ученического проекта «Живой градусник» |
|
|
|
3. Контекстные задания по математике для 5-6 классов и инструментарий отслеживания уровня сформированности математической компетентности по теме «Обыкновенные дроби» |
|
ВВЕДЕНИЕ
Российское общество сегодня переживает период глубоких структурных, в том числе социокультурных изменений. Этот процесс не может не затрагивать сферу образования и воспитания.
Главная задача российской образовательной политики – обеспечение современного качества образования на основе сохранения его фундаментальности и соответствия актуальным и перспективным потребностям личности, общества и государства. Основные принципы образовательной политики в России определены в Законе Российской Федерации «Об образовании», а также в Федеральной программе развития образования.
Основываясь на документах «Стратегии модернизации содержания образования» [8], «Концепции модернизации российского образования на период до 2010 года» [4], можно отметить, что происходит резкая переориентация оценки результата образования с понятий «подготовленность», «образованность», «общая культура», «воспитанность», на понятия «компетенция», «компетентность обучающихся», «способность к адаптации в новых условиях». Современный уровень отношений в обществе характеризуется возрастанием требований к уровню развития личности.
В национальной образовательной инициативе «Наша новая школа» также подчеркнуто, что требования к результатам должны включать не только знания, но и умения их применять. В число таких требований должны войти компетентности, связанные с идеей опережающего развития, все то, что понадобится школьникам и в дальнейшем образовании, и в будущей взрослой жизни.
Модернизация школьного образования ориентирует на развитие познавательной самостоятельности учащихся, формирование у них умений исследовательской деятельности. Одна из задач сегодня – формирование молодого человека с критическим, нестандартным мышлением, способного к поиску взвешенных решений, основанных на самостоятельном исследовании окружающего мира. Такие люди будут определять успехи нашей страны в будущем.
Таким образом, компетентностный подход (В.А.Болотов, А.В. Вишнякова, С.Г. Воровщиков, И.А.Зимняя, А.В. Хуторской, И.С. Якиманская, А.Л Андреев, А.Дахин, Г.К. Селевко и др.) ложится в основу обучения в общеобразовательной школе.
По результатам международного тестирования PISA-2006, ориентированного на проверку сформированности компетентностей в различных циклах (естественнонаучный, математический, гуманитарный), Россия набрала балл ниже среднего по уровню сформированности математической компетентности. При этом результаты учащихся начальной школы достаточно высоки, что говорит о низком уровне преемственности при переходе с первой ступени обучения на вторую.
Исходя из выше сказанного, находим противоречие между необходимостью формирования математической компетентности учащихся и недостаточно разработанной системой приемов, методов и форм реализации данного направления на средней ступени обучения.
Моя работа «Контекстное обучение как средство формирования математической компетентности учащихся 5-6 классов» посвящена разрешению данного противоречия.
Цель работы: обобщение системы работы по внедрению контекстного обучения как средства формирования математической компетентности учащихся 5-6 классов.
Для достижения поставленной цели и решения проблемы выделены следующие задачи:
-
Провести анализ теоретического состояния и практического опыта по вопросам формирования математической компетентности школьников.
-
Осуществить внедрение контекстного обучения как средства формирования математической компетентности учащихся 5-6 классов в учебный процесс.
-
Разработать и обосновать систему контекстных заданий, направленную на формирование математической компетентности учащихся 5-6 классов.
-
Разработать инструментарий по оценке уровня сформированности математической компетентности учащихся 5-6 классов.
-
Провести опытно-экспериментальное исследование, направленное на проверку влияния методики контекстного обучения на формирование математической компетентности учащихся 5-6 классов.
Объектом исследования выступает процесс обучения математике в 5-6 классах общеобразовательной школы в рамках компетентностного подхода.
Предмет исследования: технология контекстного обучения как средство формирования математической компетентности учащихся 5-6 классов.
Контекстное обучение разрабатывается более 25 лет А.А. Вербицким, однако, лишь для высшего образования. В средней школе методические разработки внедрения технологии контекстного обучения недостаточны для полной реализации, что обуславливает актуальность моей темы, её практическую значимость и новизну.
ГЛАВА I. КОНТЕКСТНОЕ ОБУЧЕНИЕ КАК СРЕДСТВО ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКОЙ КОМПЕТЕНТНОСТИ ШКОЛЬНИКОВ
-
Теоретическое обоснование компетентностного подхода в образовании
По мнению А.Л.Андреева: «В некотором смысле компетентностная парадигма как бы представляет в сфере образования то, что называют современностью, и в этом смысле она противопоставляется несовременному, архаическому, отжившему. Исторические рубежи современности при этом компетентностная модель образованности соотносится с динамичным "открытым" обществом, в котором продуктом процессов социализации, обучения, общей и профессиональной подготовки к выполнению всего спектра жизненных функций должен стать ответственный индивид, готовый к осуществлению свободного гуманистически ориентированного выбора.» [1, C.2]
Что же понимают под компетентностью? Компетентность-это способность решать возникающие в различных сферах жизни конкретные проблемы. Такой подход предполагает наличие знаний, способностей обладать определенными личностными качествами и уметь в любой момент найти и отобрать нужные знания для решения проблемы.
Компетентностный подход – это деятельностный подход. «Под компетентностью чаще понимается интегральное качество личности, проявляющееся в общей способности и готовности её деятельности, основанной на знаниях и опыте, которые приобретены в процессе обучения и социализации и ориентированы на самостоятельное и успешное участие в деятельности» [7, C.8].
Традиционные методы обучения направлены, в основном, на усвоение учащимися большого объема знаний, полученных в готовом виде от учителя. Умения при такой методике отрабатываются, по принципу «Делай как я», то есть по образцу, предложенному учителем, а навыки формируются в результате решения большого количества аналогичных задач, что исключает самостоятельную работу учащихся с первоисточниками и дополнительной литературой. В результате недостаточно развиваются творческое отношение к делу и самостоятельность при решении задач. Тенденция гуманизации образования требует поставить в центр процесса обучения личность ученика. Современному учителю, необходимо использовать методики обучения, направленные на персонифицированную личность объекта обучения. Таким образом, на современном этапе развития школьного образования одним из основных направлений является решение проблемы разработки эффективных методов преподавания и обеспечение качественного усвоения знаний учащимися.
-
Контекстное обучение как средство формирования математической компетентности учащихся
Социологи и ученые педагоги признают, что ценности сегодня сменились: и на коне не тот, кто много знает, а тот, кто умеет этими знаниями с толком распоряжаться и поэтому наша задача, задача педагогов не только научить детей, но и уметь применить свои знания в современной жизни.
Моя работа направлена на формирование математической компетентности учащихся на уроках математики в 5-6 классов.
Понятие математической компетентности отображено в различных источниках.
По мнению Г.Селевко: «математическая компетентность – это умение работать с числом, числовой информацией (владеть математическими умениями)» [7, C. 139].
По мнению ученых - исследователей, разработавших материалы по оценке знаний и умений для международной программы РISA, «математическая компетентность - это наиболее общие способности и умения, включающие математическое мышление, письменную и устную математическую аргументацию, постановку и решение проблемы, математическое моделирование, использование математического языка, современных технических средств» [5, C. 132].
Таким образом, становится ясным тот факт, что математическая компетентность - это владения математическим умениями. Можно утверждать, что математическая компетентность - это в совокупности математические знания, умения, навыки + опыт практической деятельности, умение применять «зун» на практике, в окружающей действительности.
В исследовании PISA выделяются три уровня математической компетентности: уровень воспроизведения, уровень установления связей, уровень рассуждений.
Формирование математической компетентности на уроках предполагает обучение с использованием приемов, направленных на необходимость использования внешних и внутренних знаний, умений учащихся, включения в активную деятельность по решению той или иной проблемной ситуации, решению контекстных заданий. Реализация этого возможно при осуществлении контекстного обучения в учебном процессе.
Что же подразумевает собой контекстное обучение?
По мнению А.Вербицкого: «контекстное обучение выступает концептуальной основой реализации компетентностного подхода в образовании».
Контекстное обучение предполагает максимально широкое введение в учебный процесс видов, форм и методов деятельности, позволяющих перейти от преимущественно информационных форм к активным методам и формам обучения с включением элементов проблемности, научного поиска, широкого использования резервов самостоятельной работы обучающихся [3, С. 41].
В центре теории контекстного обучения находится понятие контекста.
Контекст – это система внутренних и внешних условий жизни и деятельности человека, которая влияет на восприятие, понимание и преобразование им конкретной ситуации, придавая смысл и значение этой ситуации как целому, так и ее компонентам. Внутренний контекст представляет собой индивидуально-психологические особенности, знания и опыт человека. Внешний контекст – предметные, социокультурные, пространственно-временные и иные характеристики ситуации, в которых он действует [3, С. 41].
В качестве основных принципов контекстного обучения были выбраны следующие: определение обучающегося как активного субъекта познания; его ориентация на самообразование и саморазвитие; опора на субъективный опыт учащегося; индивидуальная направленность образовании.
Анализируя данные анализа действующих учебников по математике можно сделать вывод о необходимости создания дидактических материалов для качественного осуществления контекстного обучения математике в 5-6 классах.
Для разрешения этой проблемы и реализации контекстного обучения на уроках математики мной разработаны следующие материалы для 5-6 класса: контекстные задания, фрагменты уроков с применением ИКТ, темы и содержание ученических проектов для 5-6, контрольные работы для отслеживания уровня сформированности математической компетентности. Подтверждение результативности отражены в результатах мониторинга.
ГЛАВА II. ВНЕДРЕНИЕ КОНТЕКСТНОГО ОБУЧЕНИЯ КАК СРЕДСТВА ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКОЙ КОМПЕТЕНТНОСТИ УЧАЩИХСЯ 5-6 КЛАССОВ В УЧЕБНЫЙ ПРОЦЕСС
2.1 Приемы и методы контекстного обучения математике
Для реализации контекстного обучения математике необходимо проводить внедрение основных приемов, методов, принципов контекстного обучения во все направления учебного процесса. На уроках осуществление контекстного обучения возможно на всех этапах урока: от подготовительного до изучения нового материала и его закрепления. Во внеурочной деятельности реализация элементов контекстного обучения возможно при осуществлении проектной деятельности учащихся.
Таким образом, на уроках математики я применяю различные методы и приемы для развития творческих способностей и сформирования математической компетентности учащихся. В своей работе я использую:
Методы: проектный, проблемный, поисковый, развивающий, исследовательский.
Приемы: ролевая игра, творческая проектная деятельность, создание проблемной ситуации, выполнение развивающих заданий, воображаемое путешествие, реферат, опережающее задание, использование мультимедийных средств обучения.
2.2 Методика изучения нового материала в рамках контекстного обучения
Проиллюстрируем осуществление реализации контекстного обучения в математике на примере изучения нового материала в 6 классе по теме «Центральная симметрия» на подготовительном этапе, этапах изучения нового материала и закрепления.
1) Подготовительный этап
На предыдущем уроке математике детям предлагается домашнее задание под названием «Праздничный стол», следующего содержания: вместе с родителями «накрыть» праздничный стол, оформив на альбомном листе схему расстановки одного горячего блюда, четырех салатов. Сделать это нужно красиво, эстетично. Можно принести свои рецепты данных блюд. В зависимости от внутренних условий каждый предлагает свой способ оформления.
2) Этап изучения нового материала
Изучение нового материала осуществляется последовательно:
-
Рассматриваются различные модели оформления праздничного стола, выделив те рисунки, на которых расстановка выполнена по правилам центральной симметрии. Например: Г- горячее блюдо, С – салат и т.д. (рис. 1)
Рис. 1
-
Выделяются общие свойства рисунков, выполненных по правилам центральной симметрии, отмечается гармоничное расположение и эстетичность оформления. Тем самым детьми выделяются свойства центрально-симметричных фигур.
-
По схеме «ученик - учитель - ученик» формулируется определение центрально-симметричных фигур. Строится математическая модель (две центрально-симметричные точки).
-
Предлагается выбрать из предложенных рисунков те, на которых используется центральная симметрия (рис. 2).

Рис. 2
3) Задания на закрепление изученного материала
Мы соглашаемся с уровнями математической компетентности, предложенные в исследовании PISA и сформулированные выше. В соответствии с ними составлены следующие задания для успешного закрепления нового материала.
Задание 1 уровня. Приведите примеры геометрических фигур, имеющих центр симметрии (возможные варианты примеров: квадрат, ромб и другие).
Задание 2 уровня. Начертите треугольник АВС, отметьте точку О и постройте треугольник, симметричный треугольнику АВС относительно этой точки, если: а) точка О – вне треугольника; б) точка О – внутри треугольника; в) точка О – середина стороны АВ; г) точка О – совпадает с вершиной А.
Задание 3 уровня. Нарисовать в тетради 3 примера орнамента с элементами центральной симметрии: 1) орнамент, связанный с национально-региональным компонентом (ханты-мансийский орнамент); 2) национальный; 3) придумать свой. Показать центральную симметрию на одном из фрагментов (умеющим работать с компьютером, дается возможность сделать его в электронном виде дома).
Таким образом, на каждом этапе, начиная от домашнего задания, являющегося подготовительным этапом, до изучения нового материала и этапа его закрепления, учащиеся принимают активное участие в учебном процессе. Ребенок для выполнения заданий привлекает все имеющиеся в его распоряжении знания, способы действия, актуализация которых позволяет производить анализ введенных понятий. Вместе с тем в контексте проблемы выявляются новые связи и отношения между элементами, такие условия проблемы, которые не были заданы, благодаря чему происходит расширение поиска возможных средств решения, достижения поставленной цели. Реализация найденных закономерностей в итоге сводится в одних случаях к выполнению операций, связанных с практической деятельностью по изготовлению создаваемой конструкции, в других - к выполнению вычислений, в третьих – к построению системы доказательств, обосновывающих достигнутое решение [15, С. 193].
2.3 Проектная деятельность учащихся как средство контекстного обучения математики в 5-6 классах
Одним из методов реализации контекстного обучения математике является метод проектов. Понятие проекта достаточно широко введено в литературе, потому рассмотрим лишь его определение и место в учебном процессе, организованном по принципам контекстного обучения.
Проект – (от лат. projectus, в буквальном переводе – брошенный вперед), 1) реалистичный замысел, план о желаемом будущем; 2) совокупность документов (расчетов, чертежей, макетов) для создания какого-либо продукта, содержит в себе рациональное обоснование и конкретный способ осуществления; 3) метод обучения, основанный на постановке социально-значимой цели и её практическом применении.
Мной разработана система ученических проектов, которые выполняются к темам изучаемого материала и направлены на достижения следующей цели: способствовать развитию творческих способностей, умений добывать необходимую информацию, самостоятельно анализировать её и представлять в виде единого целого продукта; развитию интереса к математике, привитию ученикам математической культуры и расширению кругозора учащихся. В содержание проектов входят задания опережающего характера.
Организация проектной деятельности предполагает разбиение класса на творческие группы по 4-5 человек, которые совместно осуществляют выполнение поставленного перед ними задания.
Тематика проектов для 5,6 класса:
-
Проект "Обыкновенные дроби. Исторический экскурс"
-
Проект «Сказка "В царстве геометрических фигур"
-
Проект "Проценты. Исторический экскурс"
-
Проект "Родная школа помещается в ладони" (создание макета здания школы), тема «Масштаб», «Прямоугольный параллелепипед»
-
Проект "Положительные и отрицательные числа вокруг нас", "Положительные и отрицательные числа. Исторический экскурс"
-
Проект "Живой градусник"
-
Проект "Параллельные прямые"
-
Проект "Координаты. Откуда? Где? Зачем? "
-
Проект "Её величество - Пропорция"
Задание для выполнения проекта творческой группе учащихся с указанием основных требований, критериев оценивания выдается в виде информационной карты. Пример информационной карты представлен в приложении.
2.4 Методические рекомендации для работы над контекстными заданиями по математике для 5-6 классов
В рамках исследования мной разработаны контекстные задания по математике для 5-6 классов по темам «Обыкновенные дроби», «Десятичные дроби», «Положительные и отрицательные числа».
В процессе изучения математики огромную роль играет решение задач. Дело не только в применении полученных знаний на практике. По мнению ведущих методистов, без решения задач невозможно овладеть теорией, так как процесс решения задачи позволяет раскрыть взаимосвязь основных математических понятий и свойств между собой, а также окружающей нас действительностью.
Правильная постановка и подбор тематики задач и упражнений в обучении математике во многом определяет современную методику преподавания. Процесс решения задачи может служить различным целям обучения, задачи могут быть использованы при изучении новой темы, для самостоятельного установления учащимися какого-либо математического факта.
Задачи могут быть предложены учащимся с целью глубокого усвоения теоретического материала или выработки необходимых умений и навыков. Например, при изучении темы: «Десятичные дроби» можно предложить учащимся следующую задачу:
«В бочке 180 литров бензина. В первый день было израсходовано 0,6 этого количества. Сколько литров бензина осталось в бочке?»
Рассмотрим возможный сценарий фрагмента учебного занятия:
|
Деятельность учителя |
Деятельность учащихся |
|
1. Изучите содержание задачи 2.Определите, исходя из данной ситуации тип задачи. 3.Составьте краткую запись 4.Сформулируйте правило
5.Каков план решения задачи?
6.Запишите решение данной задачи
7. Существуют ли другие способы решения данной задачи?
8. Измените вопрос в задаче так, чтобы она решалась в одно действие
9. Измените условие задачи так, чтобы она решалась в одно действие
10.В качестве домашнего задания: Составьте аналогичную по способу решения задачу по теме: «Животный мир Африки». |
1.Повторно читают задачу. 2. Задача на нахождение дроби от числа. 3. Составляют краткую запись. 4.Проговаривают правило нахождения дроби от числа 5.В начале, применяя правило, найдем количество израсходованного бензина, а затем вычтем полученный результат из 180.
6.1) 180*0,6=108(л) израсходовали 2)180-108=72(л) осталось. 7.Другой способ: Все количество бензина примем за 1. Тогда решение будет таким: 1)1-0,6=0,4 (ч) бензина осталась 2) 180*0,4=72(л) бензина осталось. Ответ: 72 литра.
8.Сколько литров бензина было израсходовано в первый день?
9.В бочке было 180 литров бензина. После того, как в первый день израсходовали часть бензина, в бочке осталось 0,6 от первоначального количества. 10.Для выполнения данного задания нужно взять учебник по географии или энциклопедию. Возможный вариант: «Стада антилопы гну способны проходить огромные расстояния в поисках воды и пищи. Одно такое стадо прошло в течение нескольких дней путь в 200километров. В первый день им было пройдено 0,6 пути. Сколько километров осталось пройти антилопам туда, где идет дождь и много растительности?»
|
Подобные домашние задания позволяют возбуждать и развивать интерес не только к математике, но и к другим предметам, например, биологии, географии.
Задачи могут использоваться при обучении учащихся деятельности поисковой и творческой. Это способствует развитию у учащихся математического мышления. Например, при изучении темы «Среднее арифметическое» можно предложить такую задачу: «В семье работают отец, сын и дочь. Отец заработал за месяц 40 тысяч рублей, сын -20 тысяч рублей, а дочь-15 тысяч рублей. Каков средний заработок среднего члена семьи?»
В качестве домашнего задания можно предложить следующее:
Выясните, сколько денег заработали за прошлый месяц члены вашей семьи. Используя полученные данные, составьте и решите задачу, аналогичную исходной.
Разработанные задания представлены дифференцированно. Для удобства работы все составленные задания разделены по темам: «Действия с обыкновенными дробями», «Действия с десятичными дробями», «Действия с положительными и отрицательными числами».
Также разработан инструментарий, позволяющий учителю определить уровень сформированности у учащихся математической компетентности.
Возможно, такой подход в обучении позволит снять назревшее противоречие между необходимостью формирования у учащихся математической компетентности и реально сложившейся практикой обучения, позволит сформировать устойчивый интерес к предмету.
ЗАКЛЮЧЕНИЕ
Результаты эксперимента по внедрению контекстного обучения в учебный процесс за 2011-2012 учебный год позволяют сделать следующие выводы:
- благодаря использованию технологии контекстного обучения соблюдена преемственность при переходе учащихся на следующую ступень обучения, что подтверждается результатами успеваемости учащихся;
- организация учебного процесса на основе контекстного обучения математике позволяет повысить уровень математической компетентности учащихся 5-6 классов.
- внедрение контекстного обучения способствовало повышению познавательного интереса к предмету, что подтверждается результатами анкетирования учащихся.
Мониторинг успеваемости экспериментальной группы учащихся
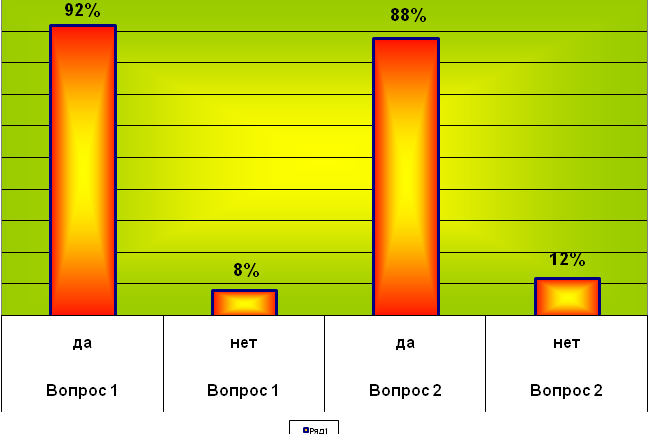
Анкетирование в контрольной и экспериментальной группах
«Познавательный интерес к предмету «математики»
|
Вопросы |
да |
нет |
|
1. Нравиться ли тебе преподавание математики? |
92% |
8% |
|
2. Пригодятся ли тебе в будущем знания, полученные на уроках математики? |
88% |
12% |
СПИСОК ЛИТЕРАТУРЫ
-
Андреев А. Л. Компетентностная парадигма в образовании: опыт философско-методологического анализа // Педагогика. - 2005. - № 4. – С. 19-27.
-
Вербицкий А. Гуманизация, компетентность, контекст – поиски оснований интеграции // «Alma mater» (Вестник высшей школы). – 2006. № 5. – С. 19-25.
-
Вербицкий А. Контекстное обучение в компетентностном подходе // Высшее образование в России. – 2006. № 11. – С. 39-46.
-
Концепция модернизации российского образования на период до 2010 года. – М., 2002
-
Краснянская К.А. Оценка математической грамотности 15-летних учащихся (PISA-2006) // Школьные технологии. – 2008. № 3. – С. 161-171.
-
Ларионова О.Г. Интеграция личностно-центрированного и компетентностного подходов в контекстном обучении (на материале подготовки учителя математики). – Автореферат на соискание ученой степени доктора педагогических наук, Москва 2007
-
Селевко Г. Компетентности и их классификация \\ Народное образование. – 2004. - № 4. – С. 138-142.
-
Стратегия модернизации общего образования. Материалы для разработки документов по обновлению общего образования. - М., 2001. С.34
-
Шквыря Е.Л. Конструирование математических задач: Учебное пособие / сост. Е.Л.Шквыря. Нижневартовск: НГГУ, 2007. – 27 с.
ИНТЕРНЕТ – ИСТОЧНИКИ
1.http://www.edu.ru – Министерство образования РФ
-
http://sc.nios.ru/about/ - коллекция цифровых образовательных ресурсов для учреждений общего и начального профессионального образования.
ПРИЛОЖЕНИЯ
|
Приложение 1 Методическая разработка урока математики в 6 классе по теме «Умножение обыкновенных дробей» |
|
|
|
Предмет: |
математика |
|
|
Класс: |
6 |
|
|
Тема: |
Умножение обыкновенных дробей |
|
|
Тип: |
Урок изучения нового материала |
|
|
Цели: |
- повторить основные действия с обыкновенными дробями, вывести правило умножения обыкновенных дробей, закрепить при выполнении заданий, проверить уровень усвоения материала; - способствовать развитию логического, аналитического, критического мышления; интереса к математике; - способствовать воспитанию умений работать в парах, самостоятельно, коллективно; - способствовать формированию математической компетентности учащихся. |
|
|
Методы: |
проблемно-поисковый, исследовательский |
|
|
Оборудование: |
ПК, интерактивная доска, карточки для игры «Лото», карточки для самостоятельной работы по новой теме, мел, доска. |
|
|
Формы работы: |
самостоятельная, работа в парах, фронтальная работа. |
|
|
План урока: |
1. Организационный момент (2 мин.) 2. Актуализация знаний – игра «Лото» (6 мин.) 3. Изучение нового материала (5 мин.) 4. Закрепление изученного материала (7 мин.) 5. Проверочная работа (8 мин.) 6. Решение практической задачи (7 мин.) 7. Рефлексия урока (2 мин.) 8. Домашнее задание (3 мин.) |
|
Ход урока:
|
Деятельность учителя |
Деятельность учащихся |
Оформление доски |
|
1. Организационный момент |
||
|
Здравствуйте, дорогие ребята! Садитесь! (приветствие)
Я рада приветствовать Вас на уроке математики и прошу обратить внимание на доску. Прочитай, Полина, что написано.
Как Вы понимаете это высказывание?
Абсолютно точно! Это высказывание будет девизом нашего сегодняшнего урока! Мы будем мыслить, рассуждать, исследовать и только так получать знания по математике! А какую тему мы сейчас изучаем, какую область математики мы «осиливаем» сейчас?
Что из этого раздела мы уже знаем и умеем?
Чтобы продуктивно работать на уроке нам нужно достать из наших сундучков знания, которые мы уже имеем предлагаю Вам игру «Лото». |
(присаживаются)
Дорогу осилит идущий, а математику мыслящий!
(пример ответа ученика) Я понимаю это так: если человек знает куда идти, то он осилит дорогу, также и в математике, если ты мыслишь, то встречаясь с проблемой, всегда сможешь найти способ её решения!
Мы изучаем тему «Обыкновенные дроби».
Мы умеем складывать дроби с одинаковыми, разными знаменателями, умножать и делить на натуральное число. |
|
|
2. Актуализация знаний – игра «Лото» (работа в парах, фронтальная работа) |
||
|
(Проводится инструктаж игры «Лото») Необходимо выполнить задания на листе, полученный результат найти на соответствующей карточке и приложить её обратной стороной к заданию. В результате получится шифр. Если какое-то задание Вы выполнить не можете, положите на него знак «?». (Контролирует выполнение заданий)
(Фронтальная работа, вместе с учащимися заполняют табло на доске, анализируют шифр)
(Подводит учащихся к формулировке проблемного вопроса – как умножить обыкновенную дробь на дробь)
Что ж, сегодня наши мыслительные операции будут направлены на то, чтобы найти ответ на это проблемный вопрос, этому и посвятим наш урок. Итак, тема нашего урока «Умножение обыкновенных дробей». Курс задан, какова цель урока? |
(Внимательно слушают, задают вопросы, если они есть).
(Выполняют задания, пара, заполнившая карточку «Лото» поднимает руку, после того как большинство выполнили задание – фронтальная проверка)
(В результате работы приходят к проблемному вопросу – как умножить обыкновенную дробь на дробь, так как решить последний пример им не удалось, в силу того, что задание новой не изученной темы)
(формулируют с учителем тему урока, записывают её в тетрадь)
Научиться умножать обыкновенные дроби, вывести правило умножения обыкновенных дробей. |
|
|
3. Изучение нового материала (фронтальная работа) |
||
|
Для достижения цели и получения ответа на проблемный вопрос предлагаю Вам выполнить небольшое исследование. Обратите внимание на доску. Охарактеризуйте условие и данные.
Как найти площадь данного прямоугольника?
Что произойдет с площадью прямоугольника, если длину и ширину одновременно уменьшить в 10 раз?
Как это можно записать в виде равенства с обыкновенными дробями?
Но ребята, посмотрите внимательно, что у нас получилось – сами того не предполагая мы выполнили умножение обыкновенных дробей! Проанализируйте равенство, выделите закономерности- как же выполнить умножение обыкновенных дробей. (по схеме: УЧЕНИК-УЧИТЕЛЬ-УЧЕНИК формулируется правило)
Молодцы!!! Вот и наше открытие! Запишем правило в тетради в буквенной форме.
|
Дан прямоугольник со сторонами 4см и 5 см. Нужно найти площадь прямоугольника.
Нужно длину умножить на ширину и получится 20 квадратных сантиметров.
(Выслушиваются ответы) Площадь уменьшится в 100 раз.
(внимательно изучают, предлагают свои варианты ответов)
Нужно числители перемножить и знаменатели перемножить!
(по схеме: УЧЕНИК-УЧИТЕЛЬ-УЧЕНИК формулируется правило) Чтобы умножить обыкновенные дроби нужно числители перемножить и результат записать в числитель, знаменатели перемножить и результат записать в знаменатель)
(записывают) |
4*5=20 см2
|
|
4. Закрепление (самостоятельная работа) |
||
|
Для закрепления правила, нужно… (2 ученика вызываются к доске, выполняют задания) |
решить примеры! (все решают самостоятельно, затем проводят проверку решений на доске) |
|
|
А теперь, ребята, я предлагаю Вам стать настоящими экспертами! Наш любимый стеснительный друг Петя Васечкин уже прорешал задания и доверил Вам проверку! Найдите ошибку в данных заданиях. |
(анализируют, находят ошибки и их характер) |
После определения ошибки, она выделяется анимацией на доске.
|
|
5. Проверочная работа (самостоятельная работа, взаимопроверка) |
||
|
(Раздаются карточки с заданиями, время работы 5 минут, затем взаимопроверка).
(Проводится анализ: количество выполнивших на «5», «4», характер ошибок) |
(Решают задания на карточке, подписывают их, затем обмениваются с соседом по парте и выполняют с помощью доски взаимопроверку). (Проводится анализ: количество выполнивших на «5», «4», характер ошибок) |
|
|
6. Решение практической задачи (работа в парах) |
||
|
(Предлагается на закрепление решить следующую задачу) |
(самостоятельно измеряют длину и ширину поверхности парты, выполняют действия, решают, записывают одно решение на доске) |
|
|
7. Рефлексия урока |
||
|
Какова была цель урока? Достигли ли мы цели урока? Сформулируйте правило умножения обыкновенных дробей. Решена ли проблема, поставленная в начале урока? Какие трудности возникли? Соответствовал ли наш эпиграф уроку? Вопросы? |
(Отвечают на поставленные вопросы, анализируя собственную деятельность на уроке) |
|
|
8. Домашнее задание |
||
|
Записываем домашнее задание. есть ли вопросы? (контролирует запись д.з. в дневник) |
(записывают, задают вопросы при возникновении таковых) |
|
Приложение 2
Информационная карта проекта
"Живой градусник"
|
Авторы Проекта |
учащиеся _____ класса __________________________ ____________________________ __________________________ ____________________________ __________________________ ____________________________ |
|
Срок сдачи Проекта |
|
|
Задание: 1) Изучите интересные факты о градусниках (виды, история возникновния). 2) Составьте несколько заданий, которые можно решить, используя математическую модель градусника. 3) Сделайте из ватмана «живой градусник» (размер 30см на 50см) 4) Составьте викторину по найденному материалу (минимум 7 вопросов). 5) Шаги 1, 2, 4 отобразите в презентации. |
|
|
План работы над Проектом |
|
Критерии оценки Проекта (макс. 5 баллов):
|
|
Содержание Проекта |
Презентация Проекта |
Викторина |
Защита Проекта |
Общая отметка (ср.ариф) |
|
Критерии |
- раскрытие темы; - указание литературы, других источников. |
- наглядность; - красочность. - наличие рисунков, таблиц, схем; - возможно музыкальное сопровождение. |
- содержание вопросов; - представление вопросов; - ответы опрашиваемых. |
- грамотность; - логичность; - участие всех в группе; - понимание темы; - буклет. |
|
|
Отметка |
|
|
|
|
Приложение 3
Контекстные задания по теме «Обыкновенные дроби»
1 уровень
-
Найди площадь прямоугольника, если:
а =
![]() см,
в =
см,
в =
![]() см.
Придумай задачу, аналогичную данной.
см.
Придумай задачу, аналогичную данной.
-
Составь и реши задачи, используя термины: время, скорость, расстояние.
3. Составь и реши задачу по
записи:
![]() от 200 равны у.
от 200 равны у.
4.Составь и реши задачу, используя
следующие данные: 3300км,
![]() ;
840км.
;
840км.
кг![]() )
и кратному отношению (в
)
и кратному отношению (в
![]() раза). Например: В магазине было красного
шёлка в
раза). Например: В магазине было красного
шёлка в
![]() раза больше, чем белого. Сколько метров
белого и серого шёлка было, если красного
было на
раза больше, чем белого. Сколько метров
белого и серого шёлка было, если красного
было на
![]() метров больше, чем серого?
метров больше, чем серого?
6. Составь и реши задачу по схеме:

![]()

2 уровень
1. Марина в магазине купила
![]() кг
конфет по цене 200 рублей за 1 кг. Какова
стоимость покупки девочки? Составь и
реши задачу, обратную данной.
кг
конфет по цене 200 рублей за 1 кг. Какова
стоимость покупки девочки? Составь и
реши задачу, обратную данной.
2. Составь и реши задачу, которая
бы решалась с помощью выражения: (![]() +
+
![]() )
* 2 +
)
* 2 +
![]() .
.
3.Длина прямоугольного
параллелепипеда равна 20см, а ширина на
![]() см
больше его длины и на 3 см больше высоты.
Вычислить V параллелепипеда.
Придумай и реши задачу обратную данной.
см
больше его длины и на 3 см больше высоты.
Вычислить V параллелепипеда.
Придумай и реши задачу обратную данной.
4.Предельный возраст яблони около
120 лет, что составляет
![]() предельного возраста тополя. Определить
предельный возраст тополя. Составь и
реши обратную задачу на нахождение
предельного возраста яблони.
предельного возраста тополя. Определить
предельный возраст тополя. Составь и
реши обратную задачу на нахождение
предельного возраста яблони.
5. Придумать условие задачи по
уравнению:
![]() + 2х = 12 и решить ее.
+ 2х = 12 и решить ее.
6. Придумай и реши задачу по теме: «Моя школа», которая бы решалась с помощью уравнения. Сделай проверку, решив её арифметическим способом.
3 уровень
1. Придумайте игру, которая потребовала бы от её участников знания о рациональных числах и умения выполнять действия над ними.
2. Составьте рекламу (антирекламу понятия «процент»)
3. Придумайте способ, который позволил бы каждому ученику проверить свои знания накануне контрольной работы по теме «Все действия над обыкновенными дробями»
4. Составь и реши задачу, в которой
бы искомым числом было бы
![]() .
В решении должно быть не менее 3-х
действий.
.
В решении должно быть не менее 3-х
действий.
5.Составь и реши задачу по теме: «Обыкновенные дроби», на материале русских народных сказок.
6.Составь и реши задачу по теме: «Музыка».
Рассмотрим пример контрольного среза по теме «Обыкновенные дроби», позволяющий проверить уровень сформированности математической компетентности.
|
уровень 1 |
|
|
1 |
Нарисуйте квадрат. Закрасьте
|
|
2 |
Начертите угол, градусная мера
которого равна
|
|
уровень 2 |
|
|
3 |
Масса трех чемоданов 32 кг. Масса Настиного чемодана такая же, как и масса двух других чемоданов вместе. Какова масса чемодана Насти? |
|
4 |
Билет в кино стоит 150 рублей. Все билеты на показ фильма проданы. Что еще надо знать, чтобы найти, сколько стоят проданные билеты? |
|
уровень 3 |
|
|
5 |
На двух полках стоят книги. На
верхней полке на
|
- Международный вебинар «Обучение грамоте старших дошкольников с помощью развивающих игр В. В. Воскобовича: практика реализации ФГОС и ФОП ДО»
- Контрольно-оценочная деятельность учителя начальных классов в условиях реализации ФГОС НОО
- Международный вебинар «Волонтёрство и новые воспитательные практики в школе»
- Методы и приемы формирования и оценки УУД младших школьников в соответствии с ФГОС НОО
- Организация исследовательской и проектной деятельности обучающихся начальной школы как основное требование ФГОС НОО
- Проектирование современного урока математики: реализация требований ФГОС