Урок по алгебре и началам анализа «Соотношения между тригонометрическими функциями одного аргумента»

Урок по алгебре и началам анализа
по теме: «Соотношения между тригонометрическими функциями одного аргумента»
10 класс (I курс)
Продолжительность урока - 45 минут
Разработал:
преподаватель математики
Бородина Елена Анатольевна
I квалификационная категория
г. Красный Луч
2015
Тема программы: Тригонометрические функции.
Тема урока: Соотношения между тригонометрическими функциями одного аргумента.
Цель урока: Обучающая: усовершенствовать знания учащихся по теме; формировать умения выполнять преобразования выражений, используя основные соотношения тригонометрических функций одного аргумента.
Развивающая: развивать математическую речь и логическое мышление учащихся; расширять их кругозор.
Воспитательная: воспитывать коллективизм, чувство ответственности за порученное дело.
Ожидаемые результаты: учащееся должны знать основное тригонометри-ческое тождество и следствия из него, использовать эти знания при решении примеров; выражать собственное мнение.
Оборудование: учебники, дидактический материал, мультимедийный проектор.
Тип урока: формирование и усовершенствование умений и навыков учащихся.
Ход урока
І. Организационный момент (1 мин)
Мотивация учебной деятельности учащихся. Объявление темы и целей урока.
ІІ. Актуализация опорных знаний (8 мин)
1. Устная разминка – «Алгебраический футбол». Учитель задаёт вопрос одному из членов группы. Тот отвечает: если правильно, то «пас» (право ответа) передаёт члену своей группы, называя его фамилию; если неправильно, то право ответа на следующий вопрос переходит к любому участнику другой группы.
1) Назвать основные тригонометрические функции.
2) В чём измеряются углы?
3) Как называется окружность радиусом 1 с центром в начале координат?
4) Какой знак имеет косинус в І четверти?
5) Какой знак имеет синус во ІІ четверти?
6) В каких четвертях знаки синуса и косинуса совпадают?
7) Определить углом какой четверти является угол 1790?
8) Углом какой четверти является угол -150??
9) Для каких углов не существует тангенс?
10)Для каких углов не существует котангенс?
11) Какова радианная мера угла 180??
2. Гимнастика для ума
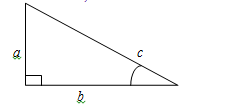
Для элементов прямоугольного треугольника установить соответствия:
1) sin А) отношение противолежащего катета к прилежащему
2) cos Б) отношение противолежащего катета к гипотенузе
3) tg В) отношение прилежащего катета к противолежащему
4) ctg Г) отношение гипотенузы к прилежащему катету
Д) отношение прилежащего катета к гипотенузе
Ожидаемый ответ:
1
 )
sin А)
отношение противолежащего катета к
прилежащему
)
sin А)
отношение противолежащего катета к
прилежащему
2 )
cos
Б) отношение противолежащего катета
к гипотенузе
)
cos
Б) отношение противолежащего катета
к гипотенузе
3 )
tg
В) отношение прилежащего катета к
противолежащему
)
tg
В) отношение прилежащего катета к
противолежащему
4) ctg Г) отношение гипотенузы к прилежащему катету
Д) отношение прилежащего катета к гипотенузе
ІІІ. Изучение нового материала (12 мин)
Ознакомление с формулами. Просмотр видеоролика, в котором рассмотрены примеры с основными способами применения соотношений между тригонометрическими функциями одного аргумента. Формулы и примеры записать в тетрадь.
IV. Формирование умений и навыков (14 мин)
1. Игра «Крестики-нолики» (проходит в парах)
Учащиеся выполняют задания самостоятельно, сверяют ответы. Затем по очереди заполняют таблицу: один учащийся правильный ответ отмечает Х, второй – 0, если ответ неверный – переход хода. Тот, кто проиграл, должен рассказать исторический факт из тригонометрии.
Задания:
-
sin2α + 2 + cos2α; 5) tgαctgα + tg2α;
-
1: (1 + ctg2 α); 6) 1- sin2α - cos2α;
-
sin2α : (cos2α – 1); 7) sinαcosαctgα – 1;
-
1 + (1 - cos2α) : (1 - sin2α); 8) (sinα - cosα)2 + 2 sinαcosα;
9) (1 + tgα)2 + (1 - tgα)2 – 1 : cos2α.
(Приложение 1)
2. Решение упражнений. Игра «Цепочка»
Учащиеся делятся на две команды. Карту заданий получают учащиеся за первыми партами. Решают пример и передают дальше. Решение предыдущего примера является началом следующего. К вниманию принимается правильность ответов и скорость (Приложение 2).
V. Закрепление изученного материала (8 мин)
Решить упражнение по примеру из видеоролика.
Найдите
![]() ,
если
,
если
![]() ,
,![]() .
.
VІ. Поведение итогов. Домашнее задание (2 мин)
Оценивание учащихся. Рефлексия: передать своё эмоциональное состояние с помощью трёх прилагательных. Кто Вам помогал в работе на уроке? Кого Вы хотите поблагодарить?
Выучить рассмотренные формулы. Составить задание на соответствие, используя эти формулы.
Литература и ссылки на источники в сети Интернет:
-
Видеоролик Саввичевой Елены youtube.com/watch?v=TI38g42WKc8
-
Математика: пiдручник для 10кл. загальноосвiтн. навч. закладiв: рiвень стандарту / Бурда М.I., Колесник Т.В., Мальований Ю.I., Тарасенкова Н.А.- К. : Зодiак-ЕКО, 2010. – 288 с. : iл.
Приложение 1
«Крестики-нолики».
-
s

1
2
3
4
5
6
7
8
9
in2α + 2 + cos2α; -
1: (1 + ctg2 α);
-
sin2α : (cos2α – 1);
-
1 + (1 - cos2α) : (1 - sin2α);
5) tgαctgα + tg2α;
6) 1- sin2α - cos2α;
7) sinα cosα ctgα – 1;
8) (sinα - cosα)2 + 2 sinα cosα;
9) (1 + tgα)2 + (1 - tgα)2 – 1 : cos2α.
Приложение 2
«Цепочка»
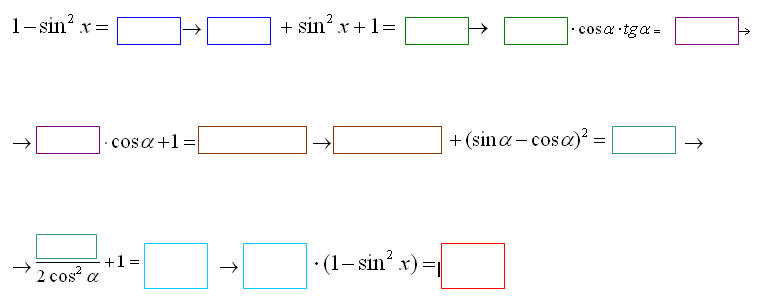
- Вебинар «Социально-коммуникативное развитие детей дошкольного возраста в условиях реализации ФОП ДО и обновлённого ФГОС ДО»
- Международный вебинар «Обучение грамоте старших дошкольников с помощью развивающих игр В. В. Воскобовича: практика реализации ФГОС и ФОП ДО»
- Международный вебинар «Волонтёрство и новые воспитательные практики в школе»
- Вебинар «Речевое развитие детей дошкольного возраста в разных видах деятельности (ФГОС ДО)»
- Вебинар «Кинезиологические игры и упражнения в развитии психических процессов дошкольников»
- Психология профессионального образования: общая характеристика





