Бойкова Анжелика Владимировна
I квалификационная категория
Новосибирская область, Барабинский р-н,
МКОУ Кармаклинская СОШ
Обобщение опыта по теме
"Практика активизации деятельности учащихся при решении задач по физике"
Актуальность
Среди практических методов обучения физике важное место принадлежит решению задач.
Решение задач в процессе обучения физике имеет многогранные функции: – средство осознания и усвоения понятий, явлений и закономерностей, средство отработки знаний и формирования умений применять их на практике, средство повторения пройденного материала, способ связи курса физики с жизнью и производством во всех его разновидностях, средство создания проблемных ситуаций, предваряющих рассмотрение нового раздела или вопроса. Решение задач имеет, кроме перечисленных обучающих функций, и ряд воспитывающих: учит трудиться, быть целеустремленным и самостоятельным, творчески активным.
Так каким образом можно вовлечь учащихся в продуктивную познавательную деятельность при решении задач по физике? Как же обеспечить усвоение умения решения задач всеми учениками? Как предупредить неуспеваемость? Как добиться результативности и при этом сохранить и укрепить здоровье ребёнка?
Один из путей решения данных проблем – системное использование приемов активизации познавательной деятельности учащихся при решении задач, которое позволяет добиться:
1. Получения максимально возможных качественных результатов в обучении физике для каждого ученика;
2. Более прочного и неформального усвоения основ физических наук;
3. Развития логического и творческого мышления.
Цель работы: Активизация познавательной деятельности учащихся при решении задач.
Задачи:
1. Изучить теоретические основы активизации познавательной деятельности при решении задач по физике.
2. Выделить наиболее значимые приемы обучения умению решать физические задачи.
3. На основе систематизации собственного опыта и опыта, описанного в
литературе, разработать систему приемов для вовлечения учащихся в процесс решения задач и поддержания интереса к решению физических задач.
1. Обучение умению решать задачи по физике
1.1. Формирование обобщенного подхода к решению задач по физике
Решение задач – нелегкий труд, требующий большого напряжения сил, он может нести с собой и творческую радость успехов, любовь к предмету, горечь разочарований, неверие в свои силы, потерю интереса к физике.
Чтобы поддержать интерес учащихся к решению задач, необходимо научить каждого ученика решать задачи.
Стараюсь подбирать задачи так, чтобы их содержание было понятным и интересным, кратко и четко сформулированным (необходимо избегать искусственности и устаревших данных в условиях задач).
Начинаем решение задач с простейших, затем постепенно переходим к более сложным задачам.
Обучение учащихся умению решать задачи провожу по следующей схеме:
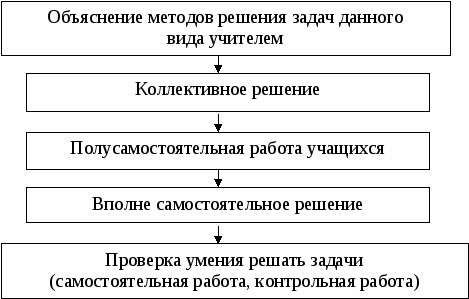
Обучение по такой схеме способствует постепенной отработке отдельных операций по решению задач, когда учитель сначала предлагает самостоятельно произвести вычисления по полученному решению в общем виде коллективно, затем при решении следующей задачи самостоятельно осуществить проверку правильности решения, в общем случае и т.д.. Учащиеся вначале самостоятельно выполняют отдельные операции под руководством учителя, затем совокупность нескольких операций переводит их на вполне самостоятельное решение задач.
Объясню, почему первые задачи разбираю сама (при этом использую беседу с активным привлечением учащихся к решению). На примере типовой задачи подробно объясняю возможные подходы, методы, приемы решения, вариации в исходных условиях, их теоретическое и практическое значение. Это позволяет с одной стороны правильно сориентировать учеников в возможных путях решения, с другой – наиболее рационально обучить всех учащихся методам решения физических задач.
Такая работа позволяет уже с 7-го класса целенаправленно обучать учащихся умению решать задачи.
В начале учебного года предлагаю ученикам общий план решения физических задач и приучаю их работать по этому плану.
План таков:
1. Внимательно прочитай и продумай условие задачи;
2. Запиши условие в буквенном виде;
3. Вырази все значения величин в единицах СИ;
4. Выполни чертеж, рисунок, схему;
5. Проанализируй, какие физические процессы, явления происходят в ситуации, описанной в задаче, выяви те законы (формулы, уравнения), которым подчиняются эти процессы, явления;
6. Запиши формулы законов и реши полученное уравнение или систему уравнений относительно искомой величины с целью нахождения ответа в общем виде;
7. Проверь решение путем действий над наименованиями единиц, входящих в конечную формулу величин;
8. Поставь числовые значения величин в полученную формулу и вычисли искомую величину;
9. Проанализируй реальность полученного результата .
С 7-го класса ввожу единые требования к технике оформления
вычислительных задач, а именно:
 Дано:
СИ: Решение:
Дано:
СИ: Решение:
а) рисунок, схема, чертеж
б) вывод конечной формулы, т.е. формулы, в которой все величины известны;
в) работа с единицами измерения
- ? величин;
табличные г) вычисления;
значения Ответ:
Приведу пример:
7-й класс, тема «Давление»
Какова высота бетонной стены, производящей на фундамент давление 440
кПа?
Дано: СИ: Решение:
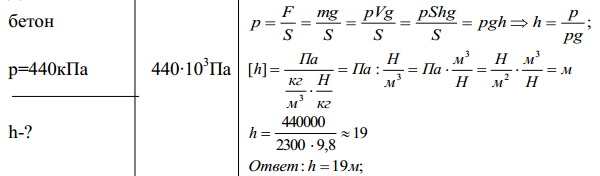
Учитывая трудности, которые испытывают учащиеся при переводе единиц измерения в СИ, для облегчения работы использую разработанные приемы, которые сокращают материал для запоминания и заставляют логически мыслить.
Покажу на примерах.
При переводе единиц измерения длины, площади и объема в СИ учу
ребят использовать приставки и знания по математике, а не заучивать, что,
например:
-
1мм2 = 0,000001м2 = 10-6 м2; 1см3 = 0,000001м3 =10-6 м3
-
Пусть S = 5 мм2 , число 5 остается, т.к. оно дано, приставка «милли»
соответствует множителю 10-3 , но у нас мм2 , следовательно, множитель возводим в квадрат (10-3)2 =10-6, т.е. получаем
5мм2=5(10-3)2м2= 5*10-6м2
-
V = 12 см3= 12*(10-2)3м3= 12 * 10-6м3
-
L=3 км=3*103 м
До использования мной этого приема многие учащиеся имели проблемы с переводом. Теперь же процент учащихся, испытывающих затруднения при таком переводе значительно уменьшился. Учащиеся легко переводят км/ч в м/с, но испытывают затруднения при переводе м/мин, см/ч и т.д. в м/с.
Учу следующему приему:
36 км/ч число оставляем, далее дробная черта: в числителе километр заменяем на равноценные метры, а в знаменателе часы заменяем на равноценные секунды. Получаем простой пример:
36 км/ч = 36* 1000м = 10м/с
3600с
аналогично поступаем и в других случаях:
240см/с = 240*10-2м = 0,04м/с
60с
30м/мин =30* 1м = 0,5м/с
60с
Этот же прием использую при переводе единиц измерения плотности в СИ.
0,9г/см3= 0,9*10-3кг = 900 кг / м3
10-6 м3
Такие нюансы помогают учащимся при решении задач, и они уже не испытывают страх ошибиться.
Для закрепления навыков работы с формулами в среднем звене, а иногда и в слабых старших классах, после введения формулы, предлагаю решения задач в общем виде, что позволяет отработать умение выражать из формулы ту или иную физическую величину.
Например: 8 класс, формула Q = cm(t2 – t1)
Задача 1: Найти количество теплоты
Задача 2: Найти удельную теплоемкость
Задача 3: Найти массу
Задача 4: Найти начальную температуру
Задача 5: Найти конечную температуру
При таком решении, чтобы избежать бездумного списывания, работы в пустую, использую такой прием: когда начинаем решать задачу, прошу учащихся самостоятельно записать в тетради основную формулу.
Далее, записываю формулу на доске. В этот момент идет зрительное запоминание формулы. Затем учащиеся самостоятельно выражают искомую величину в своих тетрадях. После этого эту же работу провожу я на доске, а ученики проверяют себя. Такую же «дублирующую» работу проводим с единицами измерения.
Данная форма работы, «ступенчатое» решение задачи, очень активизирует учащихся, заставляет их работать, учит, укрепляет веру в свои силы.
По моим наблюдениям, результат от такой работы лучше, чем, если бы задачу решили учитель или ученик у доски, а остальные в тетради.
Учителям знаком, установленный в педагогической психологии факт: перенос знаний на решение аналогичных задач происходит успешнее в том случаи, если эти знания сформированы на обобщенном уровне. Именно поэтому, обучая решению задач по той или иной теме, стремлюсь раскрыть общий подход, дать алгоритмы решения, а не учить решать каждую задачу отдельно и независимо от других. «Для обучения школьников не только значениям, но и умственным действиям важное значение имеет алгоритмизация обучения, - пишет Ю.К. Бабанский, - которое предполагает построение моделей правильных мыслительных процессов: последовательных умственных действий, кратчайшим путем ведущих к решению учебных задач».
Опыт работы учителей школ и специально проведенные исследования [6] (А.В. Усовой, Г.Н. Розенблат, Н.Н. Тулькибаевой и др.) убеждает в том, что при обучении решению задач наиболее эффективно применять алгоритмы.
1.2. Знакомство с алгоритмом решения задач на уроках физики
До урока, решение новой задачи по данной теме записываю со всеми математическими выкладками на доске. Задачу выбираю простейшую, решение, которой легко поддается алгоритмизации, т.е. составлению четкой последовательности действий. В начале урока по готовой записи на доске (четко и не спеша) объясняю учащимся решение задачи, при этом называю каждый пункт алгоритма и показываю соответствующую запись на доске, излагаю методику выполнения действий. В ходе этого этапа учащиеся ничего не записывают, так как опыт показывает, что продуктивность восприятия при ведении записи резко падает. Затем, закрыв решение задачи «крыльями» доски, ребятам предлагается воспроизвести решение в тетрадях с использованием алгоритма. Работа по времени регламентируется: на выполнение каждого пункта алгоритма отводится определенное время. Этим обеспечивается внимание учеников и выработка умения действовать в нужном темпе. Затем даю задачу, аналогичную предыдущей задаче, но с другими данными. Начинается самостоятельная работа. Те, кто считает, что усвоили решение задач данного типа, в этом решении могут не участвовать, а помогать ребятам, которые испытывают затруднения (чтобы не было лишней ходьбы по классу, учащихся посадить так, чтобы соседом по парте у сильного ученика оказался слабый).
После этого предлагаю следующую задачу. Она такого же типа, но берется из задачника. Работа объявляется «на время», т.е. те, кто решит её быстро, получат оценку.
Приведу примеры:
Алгоритм решения задач на уравнение теплового баланса.
1. Запишите уравнение теплового баланса в общем виде.
2. Определите, какие тела участвуют в тепловом обмене.
3. Изобразите графически все процессы для каждого тела, участвующего в тепловом обмене.
4. Для каждого участка графика запишите соответствующую формулу.
5. Запишите уравнения теплового баланса для данной задачи.
6. Решите полученное уравнение (или систему уравнений)
относительно искомой величины.
7. Закончите решение задачи.
Задача №1 (для обучения)
В сосуде находилось 5 кг воды и 2 кг льда при 0ºС. Какое количество100 -градусного водяного пара следует пропустить через смесь, чтобы повысить еѐ температуру до 80ºС. Теплоемкость сосуда не учитывается.
Задача №2 (для закрепления)
Для определения температуры печи в неѐ поместили стальной шарик массой 20г. Затем шарик опустили в алюминиевый калориметр массой 40г, содержащий 150г воды при температуре 20ºС. В результате температура воды в колориметре повысилась до 30ºС. Определите температуру печи.
Задача №3 (для проверки) (№645 из сборника задач Рымкевича А.П.)
В калориметр с теплоемкостью 63 Дж/К было налито 250 г масла при 120С. После опускания в масло медного тела массой 500 г при 1000С установилась общая температура 330С. Какова удельная теплоемкость масла по данным опыта?
Алгоритм решения задач на закон сохранения импульса
1. Установите, какие тела (или части одного тела) взаимодействуют между собой и образуют замкнутую систему.
2. Выполняя схематичный рисунок, укажите для каждого тела системы (или его частей) векторы импульса до и после взаимодействия.
3. Выберите оси координат.
4. Запишите закон сохранения импульса в векторной форме.
5. Запишите полученное уравнение в проекциях на оси координат.
6. Запишите уравнение или систему уравнений в алгебраической форме (через модули векторов).
7. Решите задачу в общем виде.
8. Закончите решение задачи. При анализе реальности полученного результата обратите внимание на знак (направление скорости).
Задача №1 (для обучения)
Две железнодорожные платформы, оборудованные автосцепкой, движутся навстречу друг другу со скоростями 0,3 и 0,2 м/с. Их массы равны соответственно 16 и 48 т. С какой, скоростью и в каком направлении они будут двигаться после столкновения?
Решение: (согласно алгоритму)
Задача №2 (для закрепления)
Человек, бегущий со скоростью 4 м/с, догоняет тележку, движущуюся
со скоростью 1,5 м/с и вскакивает на неё. С какой скоростью станет
двигаться тележка после этого? Массы человека и тележки соответственно
равны 60 и 25 кг.
Задача №3 (№383 из сборника Степановой Г.Н.) (для проверки осмысленности материала учащимися: в этой задаче скрытые данные- второе тело покоится). Вагон массой 30 т, движущийся по горизонтальному пути со скоростью 1,5 м/с, автоматически на ходу сцепляется с неподвижным вагоном массой 20 т. С какой скоростью движется сцепка?
На следующем уроке необходимо отработать умение решать задачи по алгоритму: это можно сделать разными способами, например, разбирается три задачи:
задача №1 – предыдущего типа – решается с использованием алгоритма;
задача №2 – сильные и средние ученика выполняют самостоятельно, а слабые – по специальным программированным письменным заданиям. В них содержатся указания, направляющие ход действий;
задача №3 - дифференцирована. Слабые ученики решают задачи предыдущего типа, но самостоятельно по вариантам. Сильные (в это же время) – повышенной трудности, написанные на карточках. Чтобы проверить умение учащихся решать задачи по алгоритму, желательно после таких уроков проводить кратковременные контрольные работы, причем стараться обеспечить каждого ученика индивидуальными карточками с условием задачи. Такая последовательность работы даёт хорошие результаты, выявляемые при проведении контрольной работы. При обучении учащихся решать задачи не следует забывать, что не может быть интересной работа, если учащийся постоянно включается в однообразную по структуре и методике деятельность. Различные приемы не только разнообразят учебный процесс, но и вызывает у учащихся удовлетворение от самого процесса труда. В этом случае основным активизирующим моментом следует считать положительный эмоциональный настрой, который возникает у учащихся при переходе на новый вид деятельности. Именно этот настрой может привести к развитию познавательных интересов учащихся.
1.2. Приемы вовлечения учащихся в процесс решения задач и поддержание интереса к решению задач
Задачи в виде таблиц 1 способ- При рассмотрении однотипных явлений составляю таблицу, в часть «клеток» которой вписываю известные значения величин, а в другой части ставлю знаки вопроса (соответствующие им величины нужно найти).
Например, в 11 классе по теме «Световые кванты» предлагаю таблицу
|
Виды излучения |
Параметры |
||||
|
λ, м |
V, Гц |
Е, эВ |
m, а.е.м. |
Р, кг·м/с |
|
|
Инфракрасное |
10-5 |
? |
? |
? |
? |
|
Видимое |
? |
5,45·1015 |
? |
? |
? |
|
Ультрафиолетовое |
? |
? |
11,3 |
? |
? |
|
Рентгеновское |
? |
? |
? |
4,3·10-6 |
? |
|
Гамма-излучение |
? |
? |
? |
? |
5,54·10-21 |
Задание: найти неизвестные величины, характеризующие разные фотоны. Использовать эту таблицу можно по-разному:
А) для обработки простейших умений применять выведенные формулы к конкретным условиям. Первую задачу (на определение характеристик инфракрасного излучения) решаем обычно с разбором у доски; вторую частично с моей помощью (помогаю тем, кто в этом нуждается); третью, четвертую и т.д. учащиеся решают самостоятельно;
Б) для контроля знаний; ведь таблица содержит сразу пять вариантов задачи;
В) для развития речи учащихся; прошу по имеющимся в таблице данным составить текст задачи и её решение, а затем произнести их вслух (или записать).
В 9,10 классах на движение предлагаю следующую задачу-таблицу
|
Вид прямолинейного движения |
а, м/с2 |
V0, м/с |
V(t) |
V (t=3с) |
S (t) |
S (t=2с) |
t,с |
V
t,с |
|
Равномерное |
? |
7 |
? |
? |
? |
? |
? |
? |
|
Равноускоренное |
? |
? |
V=5t |
? |
? |
? |
? |
? |
Задачи в виде таблиц 2 способ - Например, в 7 классе по теме «Архимедова сила» предлагаю следующую таблицу:
|
№№ |
Условие задачи |
Буква-код ответа |
|
1 |
ρ=710 кг/м3 ; V=2м3; m=? |
|
|
2 |
m=1,6т; V=20м3; ρ=? |
|
|
3 |
0,2 кН =?Н |
|
|
4 |
m=200г; Fтяж.=? |
|
|
5 |
Fтяж.=3кН; m=? |
|
|
6 |
800 дм3 =?м3 |
|
|
7 |
Vт=0,2м3; ρж=1000кг/м3; Fа-? |
|
|
8 |
0,001см2 =? м2 |
|
|
9 |
100л=?м3 |
|
|
10 |
Fтяж.=2,6 кН; Fа=2кН; R=? |
|
|
11 |
ρ=900 кг/м3; V=0,01м3; m=? |
|
|
12 |
Fа=1кН; ρж=1000кг/м3; Vт=? |
|
|
13 |
Fа=40кН; Vт=10м3; ρж=?; |
|
|
14 |
ρж=1000кг/м3; Fа=2 МН; Vт=? |
|
|
15 |
F |
|
|
16 |
F |
|
|
17 |
40г=?кг |
|
|
18 |
ρ=1800 кг/м3; m=180 кг; V=? |
|
|
19 |
Fа=18кН; Vт=3м3; ρж=? |
|
|
20 |
m=900г; Fтяж.? |
|
Учащиеся рассчитываются от 1 до 20 (зависит от числа задач в таблице), подобно тому, как это делают на уроке физкультуры. Каждый решает задачу, соответствующую его номеру. После решения предлагается ещё одна таблица, она называется «Ключ» и содержит ответы к задачам, соответствующие каждой букве
|
Ответ |
80 |
200 |
2 |
0,8 |
2000 |
0,0000001 |
0,1 |
600 |
9 |
400 |
0,04 |
300 |
1420 |
|
Буква |
О |
Л |
Ь |
Е |
Н |
А |
У |
К |
И |
М |
Р |
Ш |
Б |
Каждый ученик, пользуясь «Ключом», определяет, какой букве соответствует полученный им числовой ответ. В таблице записываются результаты. Если все учащиеся решили задачи, верно, то в колонке можно будет прочесть пословицу «Больше науки – умнее руки». Далее проводится проверка решения: каждый ученик объясняет, как он выполнил задание, приводит формулу и комментирует её. Остальные учащиеся следят за ответом. Таким образом, удается за короткий промежуток времени не только решить основные типы задач по теме, но и повторить большой материал – текущий и вспомогательный, привлечь к этому всех учащихся.
Обычно в классе учеников менее 20, поэтому в начале урока нужно предложить желающим решать индивидуальные задачи (как правило, такими желающими оказываются хорошо подготовленные ученики). Это позволяет дифференцировать работу на уроке.
Такой прием очень удобно использовать при проверке умения решать задачи (при подготовке к контрольной работе). Каждому раздается таблица с задачами. Например, в 7 классе по теме «Плотность» один из вариантов содержит таблицу:
|
№№ |
Условие задачи |
Ответ |
|
1 |
m=1,8т; ρ=1800кг/м3; V=? |
|
|
2 |
2,7г/см3=? кг/м3 |
|
|
3 |
V=0,0003м3; m=1,2кг; ρ =? |
|
|
4 |
300г=?кг |
|
|
5 |
ρ =710кг/м3; V=2м3; m=? |
|
|
6 |
100см3=?м3 |
|
Ученик решает задачи в рабочей тетради и записывает ответ. Затем предлагается «Ключ» (если есть возможность, то лучше «Ключ» размножить, чтобы у каждого ученика была своя таблица, так ему комфортнее работать). «Ключ» составляю таким образом, чтобы в ключе получилось какое-нибудь слово. Например, для предложенной таблицы «Ключ» выглядит так
|
Ответ |
4000 |
0,0001 |
1 |
270 |
0,03 |
1420 |
355 |
0,00001 |
0,00036 |
0,3 |
0,001 |
2700 |
|
Буква |
Н |
А |
У |
Г |
Ж |
Ц |
О |
К |
Е |
И |
Б |
М |
В случае правильно решенных задач получается слово «умница». На контрольной работе можно использовать эти же карточки, таблицы (так как они многовариантные). Ребята решают задачи в тетради для контрольных работ, причем задачи 1,3,5 оформляют так, как это принято. После решения выписывают ответы на черновик, тетради сдают и получают «Ключ». Ученикам уже не нужно ждать следующего урока, чтобы узнать оценку за контрольную работу, они сами могут её определить (правда, приблизительно, т.к. учитывается и оформление задач)
От простого к сложному
Есть такой тип учеников, которые, столкнувшись при решении задач с непреодолимыми для них сложностями, теряют всякий интерес к решению. Чтобы избежать таких ситуаций, необходимо подобрать для таких ребят задачи по следующему принципу:
№1 – простая задача,
№2 – аналогичная задаче №1 (для закрепления) + дополнительное действие,
№3 – аналогичная задаче №2 + дополнительное действие.
При таком подходе идет постепенное усложнение задачи, поэтому
ребята не теряют веру в свои силы.
Такой комплекс задач можно составлять самим: выбрать сложную
задачу и разбирать её на ряд простых задач (на отдельные действия).
Для реализации разноуровневого обучения на проверочных и контрольных работах использую карточки-задания трех уровней:
А. Первый уровень - задачи на знание и применение прямой формулы или физического закона.
В. Второй уровень - задачи в два, три действия на определение неизвестной величины из формулы или закона.
С. Третий уровень - задачи творческого характера, требующие знаний ранее изученного материала и комбинированных действий.
Например, для 7 класса по теме: «Механическое движение. Плотность вещества»:
МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ. ПЛОТНОСТЬ ВЕЩЕСТВА (А)
ВАРИАНТ 1
1. Определите плотность металлического бруска массой 474,5 г и объемом 65 см3.
2. Скорость течения реки равна 0,5 м/с. За какое время плывущий по течению плот пройдет путь 250 м?
З. Определите объем оловянного бруска массой 146 г.
МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ. ПЛОТНОСТЬ ВЕЩЕСТВА (В)
ВАРИАНТ 1
1. Стальная отливка объемом 25 дм3 имеет массу 150 кг. Эта отливка сплошная или полая?
2. Определите среднюю скорость автобуса на всем пути, если первые 6 км пути он проехал за 12 мин, а следующие 10 км пути - за 18 мин.
3. Как изменилась масса автомашины после того, как в нее погрузили 50 сухих сосновых брусков объемом 20 дм3 каждый?
МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ. ПЛОТНОСТЬ ВЕЩЕСТВА (С)
ВАРИАНТ 1
1. Автомашина грузоподъемностью З т должна перевезти песок объемом 40 м3. Сколько рейсов потребуется для этого сделать?
2. Определите массу воздуха, проходящего через легкие человека за 2 ч, если за 1 мин человек делает 15 вдохов и с каждым из них в его легкие поступает воздух объемом 600 см3.
3. Мотоциклист за время, равное 2 ч, проехал путь 90 км. Какова средняя скорость мотоциклиста на всем пути движения, если следующие 3ч он двигался со скоростью 50 км/ч?
Самостоятельное решение задач
Решение задач способствует развитию мышления учащихся лишь в том случае, если каждый школьник решает задачу сам, прилагая для этого определенные усилия. Широко распространенное в практике обучения так называемое коллективное решение задач у доски на деле оборачивается тем, что большинство учащихся класса бездумно переписывают решение с доски. Чтобы избежать этого очень часто использую следующий прием. Для отработки умения решать задачи по данной теме ученикам для самостоятельного решения предлагается несколько задач. Причем учащиеся могут при решении пользоваться и учебником, и рабочей тетрадью. Количество задач подбираю так, чтобы у сильных учеников не было времени на то, чтобы отвлечься. В конце урока все учащиеся сдают свои работы на проверку. Если они знают, что с работой не справились, или справились не так, как хотели бы, то у них есть возможность решить их дома. Для разбора задачи можно использовать любую литературу, помощь товарищей, родителей. Важно, чтобы поняли, как решается задача. На следующем уроке я выставляю оценки за работу выборочно: если ученик справился с задачей в классе, то оценку выставляю обязательно, если ученик дома задачу решил, то он сам решает, выставлять ему полученную оценку в журнал, или нет. Чтобы проверить, как качественно дома ученик разбирал задачу, в ближайшую проверочную работу обязательно включаю одну из задач. Такая форма работы учащимся очень нравится, так как исчезает страх перед получением плохой оценки, а знание того, что одна из задач (правда, они не знают какая) будет предложена в проверочной работе, вынуждает их учиться решать задачи по данной теме.
Уроки самостоятельного решения задач можно разнообразить: на доске написать подсказки к сложным задачам, или ответы к задачам, но расположить их хаотично (особенно это интересно для учащихся 7-8 классов).
Описанная методика обучения органично вписывается в общую систему моей работы на уроке, успешно сочетается с другими методами и формами обучения. Является наиболее эффективной и ведет к повышению качества знаний учащихся. Ведь в современных условиях психологи и педагоги оценивают эффективность урока и обучения в целом не только тем, что и сколько усвоено школьниками, но и тем, на каком уровне и как оно усвоено.
«Сочини сам»
Учащимся предлагается по данной теме составить задачу и записать её в
тетрадь. Затем ученики, сидящие на одной парте, меняются тетрадями и решают задачу соседа. После решения вновь обмениваются тетрадями: «автор» проверяет решение своей задачи. В итоге, ставится оценка: – за условие (насколько оно соответствует реальности происходящих явлений); – за правильность решения; – за проверку решения. В журнал выставляется средняя оценка. Такой подход открывает простор для творчества и поэтому он интересен для ребят.
«Найди всё, что можно»
На уроках решения расчетных задач я иногда даю задачи, в которых не указано, что надо определить, а написано: «Найди всё, что можно».
Чем полезны такая постановка вопроса и такой способ решения задач? Они развивают инициативу, мысль, помогают осмыслению материала и осознанию многочисленных связей изученных физических величин друг с другом. Кроме того, они открывают простор для творчества, поиска, а поэтому интересны для учащихся.
Приведу примеры. При изучении в 10 классе темы «Баллистическое движение» вместо объяснения предлагаю задачу: «Тело брошено под углом L к горизонту со скоростью V0. найти всё, что можно». Все с интересом приступают к работе и находят различные величины. Так как задача предлагается при изучении темы, то при решении я не только управляю ходом процесса, в результате которого оказываются решенными конкретные учебные задачи, но ещё и обучаю учащихся, в результате чего они овладевают новыми знаниями. При решении данной задачи, используя совместно построенный рисунок, учащиеся находят:
-
Время полета
-
Максимальную высоту подъема
-
Дальность полета
-
Угол, при котором дальность полета будет максимальной
-
Скорость тела в любой момент времени
-
Скорость тела в момент падения
-
Угол падения
-
Координаты тела в любой момент времени
-
Получаем уравнение траектории
Так, решая эту задачу, учащиеся знакомятся с баллистическим движением. Если в классе собраны более подготовленные дети, то задачу можно решать в общем виде. Но если класс «слабый», то лучше всего использовать в задаче конкретные числовые данные. Совместно, закончив такую большую работу, учащиеся испытывают, во-первых, восторг от того, что имея так мало первоначальных данных можно найти столько величин, а во-вторых, удовлетворение от проделанной работы.
При повторении в 10 классе молекулярной физики предлагаю задачу: «Кислород массой 6 кг занимает баллон вместимостью 5 м3и находится под давлением 300 кПа. Найти всё, что можно». Учащиеся находят различные величины в разном порядке, разными путями. Определяют плотность, среднюю квадратичную скорость движения молекул кислорода, массу молекулы газа, концентрацию молекул, количества вещества, среднюю кинетическую энергию движения молекул, температуру газа.
При решении таких задач появляется эффект соревнования, и это активизирует учащихся. Такой прием освобождает учащихся от скованности, боязни плохой оценки, порождает инициативу. В решение включаются даже слабые учащиеся.
Обязательно использую этот прием при повторении в конце учебного года. Когда семиклассникам предлагаю задачу: «Масса кирпича 1кг. Определите всё, что можно», то они стараются использовать весь багаж знаний, полученный на уроках физики. Определяют объем, силу тяжести, вес кирпича, выталкивающую силу, действующую на него в воде, силу, которую нужно приложить, чтобы удержать кирпич в воде.
Эстафета
Этот прием подразумевает предоставление учащимся ряда взаимосвязанных задач, в результате решения которых получается один итоговый ответ. Нельзя перейти к следующей задаче, не решив предыдущую.
Такой метод решения задач не только активизирует ребят, но и мобилизует их, т.к. нужно получить правильный ответ, решив серию задач.
На доске можно записать правильный конечный ответ, чтобы учащиеся могли сопоставить свой полученный результат с верным, а в случае разногласия сами постарались найти ошибку.
Т.к. чаще всего в «эстафете» использую 5 заданий, то при проверке на доске записываю и промежуточные значения. Учащиеся сами могут себя оценить, присваивая 1 балл за каждую правильно выполненную строчку. Хорошие оценки выставляю в журнал. Учащиеся, которые
не совсем успешно справились с заданием, сами могут определить над чем
им ещё нужно поработать.
При подготовке к ЕГЭ, учитывая, что в уровне В нужно дать только ответ, т.е. решать нужно очень внимательно, на доске уже не пишу конечный результат, а предлагаю его только после того, как ученик полностью справился с задачей. Учащиеся сами оценивают свой уровень подготовки.
Педагогическая эффективность приема обусловлена индивидуальной, многоплановой работой каждого учащегося (поиск, выделение нужной информации, систематизация, исправление ошибок).
Урок первых задач (идея заимствована у В.Ф. Шаталова)
Когда изучен теоретический материал по теме, приступаем к задачам. Использую такой прием: на доске заранее делаю краткую запись условия (как принято «уголком») трех- или четырех типовых задач. Тетради учащихся закрыты. Вначале анализируется первая задача, которая решается в общем виде. После разбора задачи даётся несколько минут на консультацию: у соседа по парте или у учителя. По завершении консультации всё решение с доски стирается. Аналогично разбирается вторая задача, потом третья… Затем по данным на доске ученики сами решают эти задачи, но только с подсчетами. Такая самостоятельная запись в тетрадь проводится потому, что активность мыслительной деятельности учащихся может быть невысокой, если они недостаточно «прочувствовали» условия задачи и надеются списать готовое решение с доски. Учащиеся самостоятельно решают задачи, каждый своим темпом. Так как в классе не все могут успеть решить предложенные задачи полностью, то в домашнее задание обязательно нужно включить, кроме новых задач, и последние, разобранные на уроке.
Такой метод я использую не только для обучения решению задач по
данной теме, но и для повторения и обобщения темы на основе задач.
Найдите ошибку
Этот прием доказал свою эффективность с методической точки зрения: вырабатывается критичность мышления, развивается самоконтроль ученика и др., кроме того, использование подобных заданий на уроке приучает ребят к внимательности, позволяет предупредить появление типичных ошибок, т.е. провести своеобразную профилактику ошибок.
Известно, что прямое указание учащемуся на допущенную ошибку часто малоэффективно, даже если он эту ошибку исправил. Поэтому, если ученик при решении задачи у доски допустил ошибку, а одноклассники её не заметили, то я не спешу указать на её наличие. После того, как задача решена, сообщаю, что при решении была допущена ошибка и начинается совместный поиск ошибки. Учащимся приходится зачеркивать неверное решение, решать задачу заново, при решении следующей задачи уже учитывают данный опыт.
Ошибки учащихся стихийны и неуправляемы, поэтому я иногда сама при решении задач их планирую, причем так, чтобы результат в задаче получился нереальным, и ребята сами высказали предположение о допущенном неверном решении.
Встреча с ошибкой будет происходить под контролем учителя, она будет вскрыта, выявятся причины её возникновения. Необычность ситуации приводит к тому, что ученики запоминают свои ошибочные действия (может быть даже бессознательно) и в дальнейшем стараются не допускать их.
Например, при изучении в 8 классе темы «Плавление и отвердевание кристаллических тел» вводится формула Q = λ·m. Некоторые учащиеся при дальнейшем использовании этой формулы упускают очень важный момент, а именно, то, что вычисления по этой формуле можно производить только в том случае, если тело находится при температуре плавления. Поэтому предлагаю задачу: «У меня в руках алюминиевый цилиндр. Какое количество теплоты мне потребуется для того, чтобы его расплавить?»
Ребята предлагают с помощью весов определить массу цилиндра, затем, найдя по таблице значение удельной теплоты плавления алюминия, рассчитывают количество теплоты по формуле Q = λ·m. Вызывает удивление, когда они узнают о том, что этого количества теплоты недостаточно. Начинаем искать ошибку, прошу ребят ещё раз обратиться к теоретическому материалу и сравнить с нашей задачей. Проводя сопоставления, ученики приходят к выводу, что алюминиевый цилиндр был при комнатной температуре и, чтобы его расплавить нужно сначала нагреть до 660ºС (температуры плавления), и только потом цилиндр при дальнейшем нагревании будет плавиться. В итоге получается конечная формула
Q = cm(tпл- t)+λm. В дальнейшем, решая задачу такого типа, учащиеся, прежде всего, определяет температуру плавления твердого тела, а только потом будут решать какие формы использовать.
Интересные задачи
Определенный круг физических задач способствует развитию интереса. Иногда учащихся привлекает само содержание задачи, заинтересованность в конечном её ответе. Например, как надо направить лодку, чтобы скорее перебраться на противоположный берег: перпендикулярно течению реки или под углом к нему?
Интересны для учащихся задачи с неожиданным ответом. Например, если паутину протянуть от Земли до Солнца, то какова будет её масса? (3 тонны). Какова масса телеграфной проволоки, соединяющей Москву и Санкт-Петербург? (64 тонны).
Обычно вызывают интерес задачи-«ловушки» со скрытыми данными. Например, у Я.И. Перельмана есть такая задача: «Вообразите, что вы очутились на тропическом острове Тихого океана без всяких орудий. Как сдвинули бы вы там с места груз массой 3 тонны, например гранитную глыбу 100 футов длины и 15 футов высоты? (считать, что 1 фут ≈1/3 м)
Учащиеся выдвигают невероятные предложения, между тем толщина этой глыбы 7мм. Понятно, что столь малая толщина глыбы делает её весьма неустойчивой, и она легко может быть сдвинута.
Не меньший интерес у учащихся вызывает решение задач с историческим содержанием. Например, одна из них: «В созданных Лодыгиным А.Н. первых электрических лампах накаливания (1872 г.) нагревался угольный стержень. Подсчитайте мощность шестивольтовой лампы Лодыгина, если угольный стержень имел длину 6 см и диаметр 2 мм». Учащиеся обычно предполагают, что мощность первой лампы была незначительной, и бывают поражены, рассчитав, что она равнялась приблизительно 200 Вт.
Использование софизмов и парадоксов озадачивает учеников и не оставляет их равнодушными к процессу решения задач. «Размышления над софизмами и парадоксами, как считает В.Н. Ланге [3, с.3] не нужно считать пустой тратой времени. Не случайна любовь к ним таких выдающихся ученых, как Г. Лейбниц, Л. Эйлер, А. Энштейн. Может быть, именно любовь к нешаблонным задачам развила у них способность к нестандартному мышлению». Софизмы и парадоксы помогают, активизируют учащихся на уроке, помогают при подготовке к олимпиадам. Например, при изучении понятия мощности предлагаю следующую задачу: «Велосипедист развивает силу тяги 100Н. Считая силу трения постоянной и равной 50Н, определите ускорение, и скорость велосипедиста через 20 минут после начала движения».
Ответ: а=0,5 , V=600 Значение скорости велосипедиста
приближается к скорости ружейной пули! Ответ, безусловно, неверен, хотя в самом решении ошибки нет. Ошибка состоит в допущении, что в течение 20 мин человек непрерывно развивает усилие 100Н. Нетрудно подсчитать, что для этого он должен развить среднюю мощность, приблизительно равную 30 кВт(40 л.с.). Поэтому, хотя человек может легко создать усилие 100Н, он не в состоянии поддерживать его длительное время.
Один из способов дать толчок к активной мыслительной деятельности ребят – предложить им нестандартные учебные задачи, затрагивающие реальный мир, жизненные ситуации, встречающиеся каждому человеку. Такие ситуации можно найти в книге Заслуженного учителя В.И. Елькина «Необычные учебные материалы по физике». [2] Задачник состоит из четырех разделов: «Почемучкины задачи», «Задачи Шерлока Холмса», «Занимательные вопросы Робинзона Крузо», «Вовочкины задачи». Эти задачи качественные, они помогают понять, что физика окружает нас, что ею «пропитан» весь мир. Через познание этой истины проявляется устойчивый интерес к предмету и потребность узнавать новое. Такие задачи использую по-разному: иногда разбираем их на уроке, иногда задаю на дом, часто предлагаю их в качестве дополнительного задания сильным, вручаю как «поощрение». Применяю их при повторении и закреплении пройденного на уроке, а также на внеклассных занятиях. Эти задачи интересны и взрослым, а уж у детей вызывают истинный восторг.
ЗАКЛЮЧЕНИЕ
Изучив теоретические основы активизации познавательной деятельности при решении задач по физике, убеждаемся в том, что активность учащихся в учении проявляется не в принудительном запоминании тех или иных знаний и приобретении определённых умений и навыков, а в познавательной деятельности, происходящей по собственному желанию и внутреннему побуждению, организуемой и умело направляемой учителем.
В работе сделана попытка создать соответствующую систему использования разнообразных приемов активизации познавательной деятельности учащихся при решении физических задач.
Мною были использованы практически все описанные приемы активизации учебно-познавательной деятельности, что дало положительные результаты. С 2011 года учащихся 9, 11 классов ежегодно выбирают предмет для сдачи итоговой аттестации и всегда подтверждают свои знания. Так, в 2011 год - 55% выпускников, 2012 год - 47%, 2013 год - 66%. Увеличивается число участников различных дистанционных викторин, конкурсов, проектов. Это говорит об устойчивом интересе большинства школьников к предмету, об уверенности в своих способностях и знаниях.
Рекомендации по применению результатов работы:
-
Учителю необходимо постоянно заботиться о поддержании познавательной активности учащихся.
-
Необходимо обладать достаточным арсеналом приемов активизации учебной познавательной деятельности и умением выбирать наиболее подходящие приемы, учитывая способности учащихся.
-
Регулярное использование на уроках физики системы разноуровневых задач и заданий, направленных на развитие умений и навыков, расширяет кругозор школьников, способствует развитию физико-математического мышления, повышает качество подготовленности, позволяет детям более уверенно ориентироваться в закономерностях окружающей их действительности и активно использовать свои знания в жизни.
ЛИТЕРАТУРА
-
Выготский Л.С. Умственное развитие детей в процессе обучения. Москва, 1955
-
Елькин В.И. Сайт Занимательная физика в вопросах и ответах, http://elkin52.narod.ru/
-
Ланге В.Н. Физические парадоксы и софизмы. – Москва: Просвещение, 1978
-
Остерман Л.А. Задачи на развитие физического мышления. - В кн.: Сколько нужно дров?..Подходы к обучению решению задач на тепловые явления. 8 класс. Библиотечка "Первого сентября" Серия "Физика" Выпуск 3, Москва "Чистые пруды" 2007
-
Рубинштейн С.Л. Принципы и пути развития психологии. Москва,1959
-
Сёмке А.И. Игры на уроках физики и после, 8-1классы. Библиотечка "Первого сентября" Серия "Физика" Выпуск 2, Москва "Чистые пруды" 2007
-
Усова А.В., Тулькибаева Н.Н. Алгоритмы и алгоритмические предписания по решению физических задач. – В кн.: Совершенствование процесса обучения физики в средней школе. Выпуск 2, Челябинск, 1975 г.
-
Ушинский К.Д. Собрание сочинений. Москва, 1969 г.
- Международный вебинар «Волонтёрство и новые воспитательные практики в школе»
- Международный вебинар «Обучение грамоте старших дошкольников с помощью развивающих игр В. В. Воскобовича: практика реализации ФГОС и ФОП ДО»
- Системно-деятельностный подход в преподавании физики в условиях реализации ФГОС
- Международный вебинар "Термодинамика: базовые законы физики, или Возможен ли вечный двигатель"
- Методика подготовки учащихся к Единому государственному экзамену по физике: особенности коррекции навыков решения задач учащимися
- Внеурочная деятельность: робототехнический клуб




 а,м/с2
а,м/с2
 1=1Н;
F2=0,2Н; F1 F2; R=?
1=1Н;
F2=0,2Н; F1 F2; R=?