Республика Саха (Якутия)
Открытое занятие
по алгебре и началам анализа
в 11 А классе
(социально-экономический профиль)
Тема: «Функциональный метод решения
комбинированных уравнений»
(урок-консультация)
Учитель: Бракк Елена Михайловна
СОШ №1
г. Нерюнгри - 2011 г.
Тип урока: урок комплексного применения знаний, умений и навыков по теме «Решение комбинированных уравнений»
Цели:
-
Обучающая: закрепить и углубить знания, умения и навыки учащихся по решению нестандартных комбинированных уравнений, используя свойства ограниченности функций и свойства монотонности функций.
-
Развивающая: развивать творческие способности учащихся, позновательный интерес к предмету; развивать исследовательские способности: умение анализировать, сравнивать, сопоставлять и обобщать.
-
Воспитательная: воспитывать чувство взаимопомощи, ответственности за полученный результат, упорство и настойчивость в достижении поставленной цели.
Оборудование урока:
-
Таблица «Опорные неравенства»;
-
Раздаточный материал для домашнего задания;
-
Раздаточный материал для дифференцированной работы в группах.
-
Оценочные листы деятельности учащихся в группах;
-
Таблица «Решение комбинированного уравнения графическим методом»
Подготовительный этап
За неделю до урока ученикам даются теоретические вопросы и письменное домашнее задание.
Вопросы теории:
-
Сформулировать теорему об использовании ограниченности функции к решению комбинированных уравнений;
-
Сформулировать теорему об использовании свойства монотонности функции к решению комбинированных уравнений;
-
Указать область значений следующих функций:
y = sinx; y = cosx;
y = arc sinx y = arc cosx
y = arc tgx y = arc ctgx
y = |f(x)|
![]()
![]()
![]() ,
где
,
где
![]()
![]() ,
если а>0
,
если а>0
![]() ,
если а<0
,
если а<0
y = a sinx+b cosx
Домашние задания на открытый урок
Решить уравнения:
Учащиеся класса делятся на четыре группы (по 6 – 7 человек в группе), выбираются консультанты в каждой группе из числа тех, кто занимается на «4» и «5». Во внеурочное время консультанты устно отвечают учителю на теоретические вопросы и показывают ему решение домашних уравнений. При необходимости консультанты получают у учителя консультацию по решению или оформлению задач повышенного уровня сложности. На уроке консультанты выступают в роли учителя: спрашивают, проверяют и оценивают ответы и решения учащихся, заполняют оценочные листы. Работа групп проходит под наблюдением учителя
Ход урока
Этап 1 Организационный момент.
Учитель: Одним из эффективных методов решения уравнений является метод, основанный на использовании ограниченности функций. К наиболее известным ограниченным функциям относятся некоторые тригонометрические функции; обратные тригонометрические функции; функции, содержащие модуль, степень, корень с чётной степенью и т. д. Вспомним наиболее распространённые неравенства ( на доске – таблица опорных неравенств):
─1![]() sin
x
sin
x![]() 1
─1
1
─1![]() cos
x
cos
x![]() 1
1
–π
/2![]()
![]() arc
sin
arc
sin![]() π
/2 0
π
/2 0![]() arc
cos
arc
cos![]() π
π
–π
/2![]() <arc
tg<π
/2 0<arc
ctg<π
<arc
tg<π
/2 0<arc
ctg<π
|f(x)|![]() 0;
0;
![]() ;
;
![]() ;
;
![]() где
где
![]()
![]()
![]() если a > 0; равенство
достигается при а =1.
если a > 0; равенство
достигается при а =1.
![]() если a < 0; равенство
достигается при а = –1.
если a < 0; равенство
достигается при а = –1.
![]() при
при
![]()
![]() равенство достигается при a=b.
равенство достигается при a=b.
![]()
![]()
![]()
Этап 2 Актуализация знаний учащихся.
-
Кратко обсуждаются способы и приёмы, с помощью которых решались уравнения из домашнего задания. Ребята задают вопросы учителю по заданиям более высокого уровня сложности (№6 - №7). Эти задания обсуждаются более подробно у доски теми учащимися, которые с этими заданиями справились.
Пример №6
![]()
Решение:
![]()
![]()
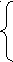
x>0
![]()
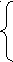
x>0
Рассмотрим функции
![]() и
и
![]() .
.
Оценим
значения функции f(x).
Поскольку х
и
![]() - взаимно-обратные величины и x
> 0, то
- взаимно-обратные величины и x
> 0, то
![]() ;
;
![]() .
.
В
силу возрастания функции
![]() на множестве положительных чисел получим
на множестве положительных чисел получим
![]() ,
т.е.
,
т.е.
![]() .
.
Итак,
![]() .
.
Оценим значения функции g(x).
![]()
![]()
![]()
![]() .
Итак,
.
Итак,
![]() .
.
Т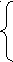 .к.
.к.
![]() ,
а
,
а
![]() при
при
![]() то
уравнение f(x)=g(x)
равносильно системе f(x)=2
то
уравнение f(x)=g(x)
равносильно системе f(x)=2
g(x)=2
![]()
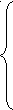
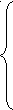
![]()
![]()
![]()
![]()
![]()
x > 0 x > 0
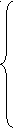
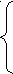
![]() x=1
x=1
![]()
![]()
![]() x>0
x>0
x > 0
Ответ: х=1.
Пример №7 Решить уравнение
![]()
Решение:
Рассмотрим
функции
![]() и
и
![]() .
.
Оценим значения функций.
![]()
![]()
![]() Итак,
Итак,
![]()
![]()
![]()
![]()
Итак,
![]() .
.
Т.к.![]() а
а
![]() ,
то равенство f(x)=g(x)
может быть
только в том случае, когда обе части
уравнения равны единице, т.е.
,
то равенство f(x)=g(x)
может быть
только в том случае, когда обе части
уравнения равны единице, т.е.
![]()
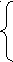
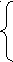
![]()
![]()
![]()
![]()
![]()
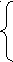
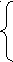
![]()
![]()
![]()
![]()
![]()
![]() .
.
Из второго уравнения системы получаем, что
![]() или
или
![]()
![]()
![]() или
или
![]()
![]()
Т.е.
![]() ,
,
![]() .
.
![]()
![]()
![]()
![]()
Подставим
значения
![]() в первое уравнение системы:
в первое уравнение системы:
![]() ;
;
![]() ;
;
![]() ;
(истинно).
;
(истинно).
Отсюда
следует, что решением системы уравнений
являются числа
![]()
![]()
Ответ:
![]()
![]() .
.
В то время, когда двое учащихся решают у доски уравнения №6 и №7 из домашнего задания, с остальными учащимися проводится «Разминка» (устные упражнения).
Найти область значений следующих функций:
Ответы:
-
f(x) = 2+|x|;
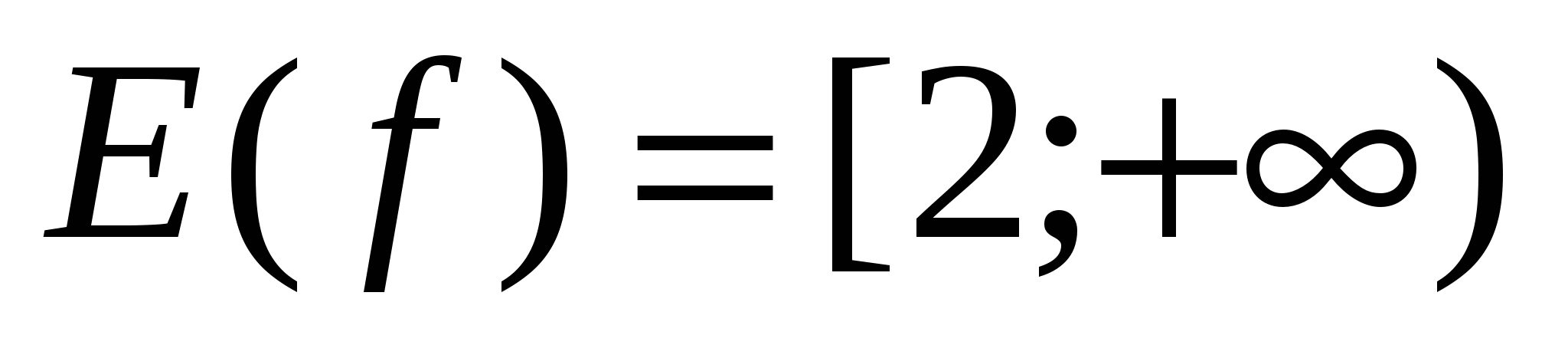
-
f(x) = 3sin²x; E(f) = [0;3]
-
f(x) = (4x-3)²+7;
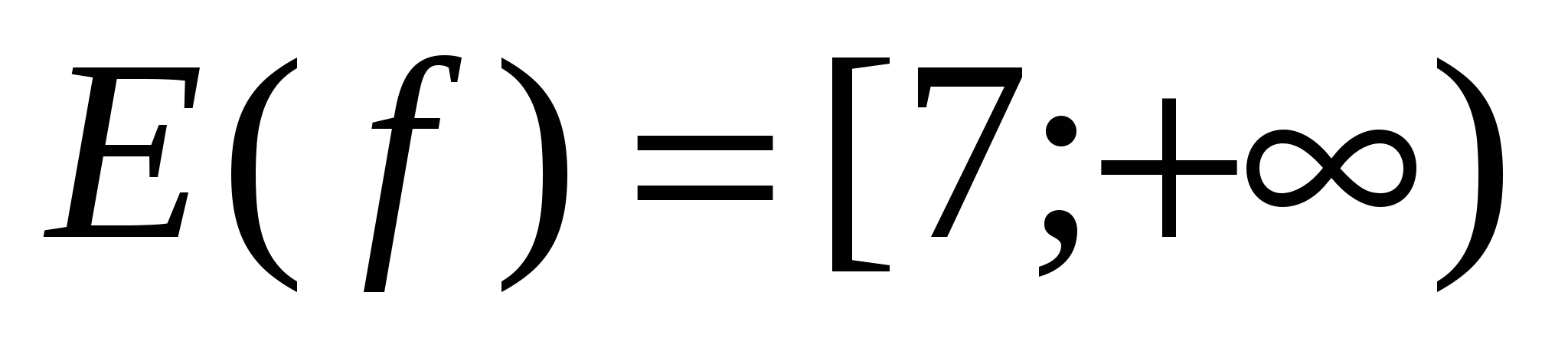
-
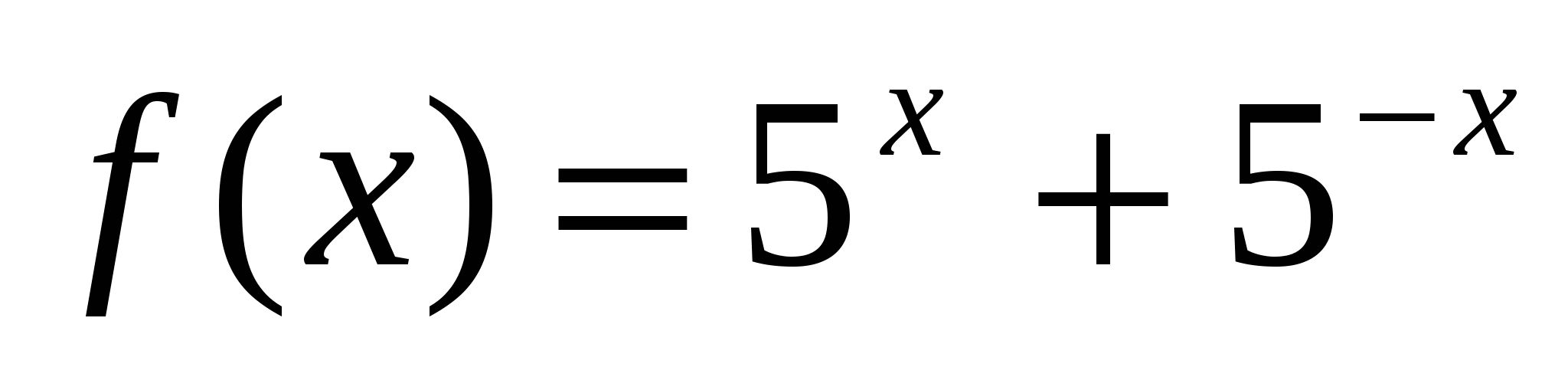 ;
;
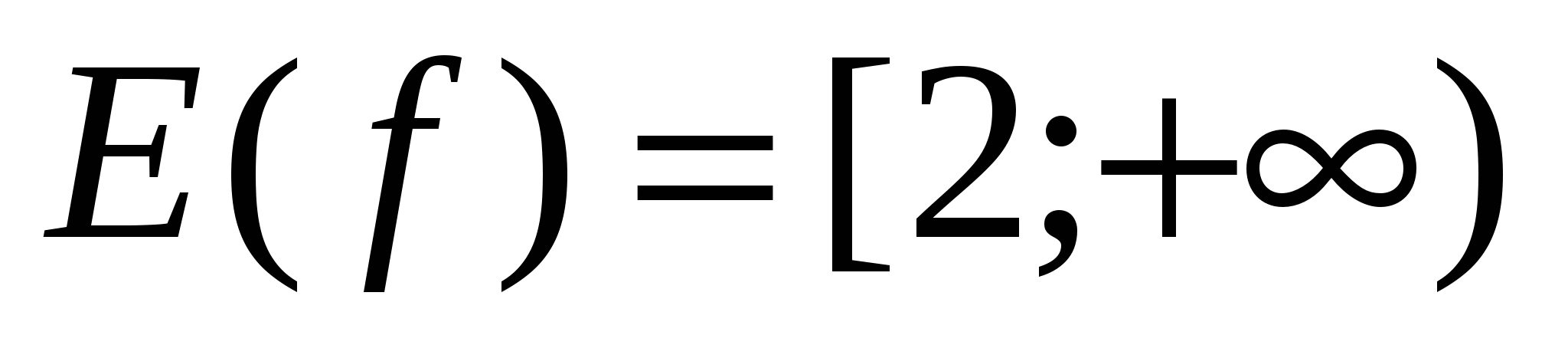
-
f(x) = tg²x+ctg²,
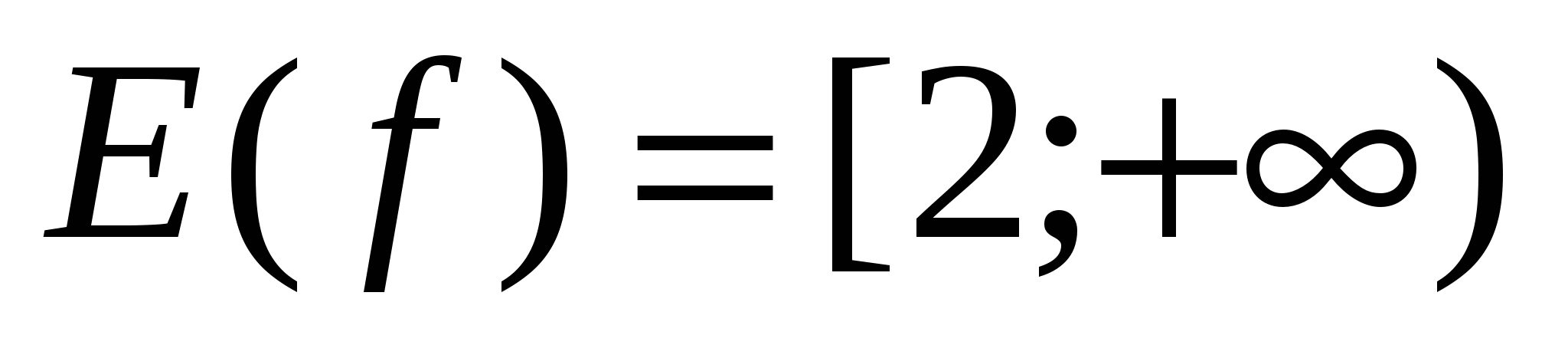
где
![]()
![]() ;
;
е) f(x) = 3sin2x – 4cos2x; E(f) = [-5;5]
ж)
![]() ;
;
![]()
з)
![]() ;
E(f)
= (0;1]
;
E(f)
= (0;1]
Этап 3 Дифференцированная самостоятельная работа в группах.
Группы получают по семь карточек, на каждой из которых записано одно из комбинированных уравнений разного уровня сложности. Учащиеся сами выбирают уровень сложности задания (всего их 3).
Карточки синего цвета – с заданиями продвинутого уровня более простого вида. Их правильное решение гарантирует ученику оценку «3».
На карточках зеленого цвета – задания продвинутого уровня более сложного вида, их правильное решение гарантирует ученику оценку «4».
На карточках красного цвета – задания повышенного уровня сложности, их правильное решение гарантирует ученику оценку «5».
Синяя карточка №1
Решить
уравнение
![]() .
.
Синяя карточка №2
Решить
уравнение
![]() .
.
Синяя карточка №3
Решить
уравнение
![]()
Зелёная карточка №4
Решить
уравнение
![]()
Зелёная карточка №5
Решить
уравнение
![]() .
.
Красная карточка №6
Решить
уравнение
![]()
Красная карточка №7
Решить
уравнение
![]() .
.
Ответы по самостоятельной работе заранее заготовлены на обратной стороне доски:
№1. x =2;
№2 х = –3;
№3 х = –1,2;
№4 х = 1,5;
№5 х = 0,25;
№6 х = 2;
№7 х = 1.
Этап 4 Устные упражнения на применение свойства возрастания (убывания) функции к решению комбинированных уравнений.
Учитель: В задании будут даны две функции, несовместимые для непосредственного аналитического решения. Необходимо будет провести нестандартные логические рассуждения для решения уравнения f(x) = g(x). В ряде случаев весьма эффективным является метод, который использует монотонность функций y = f(x) и y = g(x).
Ученики формулируют теорему:
Если функция y = f(x) непрерывна и возрастает на отрезке [a;b], а функция y = g(x) непрерывна и убывает на этом же отрезке, то уравнение f(x) = g(x) на отрезке [a;b] может иметь не более одного корня.
Учитель: Поэтому при решении уравнения f(x) = g(x) необходимо исследовать функции y = f(x) и y = g(x) на монотонность, и если одна из этих функций на отрезке [a;b] убывает, а другая функция возрастает, попытаться отбором найти единственный корень уравнения или показать, что такого корня не существует.
Пример 1 Решить уравнение
![]()
Решение:
Общая
часть областей существования функций
![]() и
и
![]() есть промежуток [-7;+∞). На этом промежутке
функция f(x)
убывает, а функция g(x)
возрастает. Следовательно, исходное
уравнение имеет не более одного корня.
Подбором находим, что х=
-2
есть промежуток [-7;+∞). На этом промежутке
функция f(x)
убывает, а функция g(x)
возрастает. Следовательно, исходное
уравнение имеет не более одного корня.
Подбором находим, что х=
-2
Ответ: х= -2.
Пример 2 Решить уравнение
![]() Ответ: не имеет
корней.
Ответ: не имеет
корней.
Примечание:
Это
хорошо видно на таблице, где построены
графики функций
![]()
![]() и
и
![]() .
.
Этап 5 Рефлексия деятельности групп (отчёт консультантов).
Оценочный лист учащихся группы
Консультант: _____________
|
№ п /п |
Ф.И.учащегося |
Вопросы теории |
Домашние задачи |
Оценка за д\з |
Защита д\з у доски |
Разминка |
Диф. с. р. |
Оценка за урок |
||||||||
|
Опорные нер-ва |
Исп. св-ва огран. |
Исп. св-в монотон. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итого |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Этап 6 Домашнее задание.
Решить уравнения:
4*.
![]()
- Международный вебинар «Волонтёрство и новые воспитательные практики в школе»
- Международный вебинар «Обучение грамоте старших дошкольников с помощью развивающих игр В. В. Воскобовича: практика реализации ФГОС и ФОП ДО»
- Вебинар «Социально-коммуникативное развитие детей дошкольного возраста в условиях реализации ФОП ДО и обновлённого ФГОС ДО»
- Международный вебинар «Цель и преимущества использования ТРИЗ-технологии в дошкольном образовании в условиях реализации ФОП ДО»
- Вебинар «Кинезиологические игры и упражнения в развитии психических процессов дошкольников»
- Психология профессионального образования: общая характеристика





