
РАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ
ДЛЯ УЧАЩИХСЯ 8 КЛАССА
Программу составил:
Учитель математики
Коктышева Ю.Г.
С. Новоцурухайтуй
2015-2016 учебный год
Пояснительная записка
Данная рабочая программа составлена на основе:
- федерального компонента государственного стандарта общего образования 2004г,
- примерной программе по алгебре и началам анализа среднего (полного) общего образования,
- федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях.
- программы по алгебре 8 класса (базовый уровень) автор А.Г.Мордкович, с учетом требований к оснащению образовательного процесса, в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования.
Нормативные документы. Документы, обеспечивающие реализацию
программы.
Закон «Об образовании РФ»
Концепция модернизации российского образования
Государственного компонента образовательного стандарта 2004 года
Примерных программ по предметам
Устава МБОУ «Новоцуоухайтуйской СОШ»
Общая характеристика учебного предмета.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
цели:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Задачи:
-
Выработать умение выполнять тождественные преобразования рациональных выражений.
-
Расширить класс функций, свойства и графики которых известны учащимся; продолжить формирование представлений о таких фундаментальных понятиях математики, какими являются понятия функции, её области определения, ограниченности. Непрерывности, наибольшего и наименьшего значений на заданном промежутке.
-
Выработать умение выполнять несложные преобразования выражений, содержащих квадратный корень, изучить новую функцию
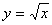 .
. -
Навести определённый порядок в представлениях учащихся о действительных (рациональных и иррациональных) числах
-
Выработать умение выполнять действия над степенями с любыми целыми показателями.
-
Выработать умения решать квадратные уравнения и уравнения, сводящиеся к квадратным, и применять их при решении задач.
-
Выработать умения решать линейные и квадратные неравенства с одной переменной; познакомиться со свойствами монотонности функции.
Место предмета в базисном учебном плане
Согласно федеральному базисному учебному плану на изучение математики в 8 классе отводится не менее 175 часов из расчета 5 ч в неделю
На изучение алгебры отводится 3 часа в неделю. Продолжительность учебного года – 34 недели. Количество учебных часов алгебры в год составляет 102 часа.
По алгебре на контрольные работы предусмотрено – 10;
Самостоятельных работ – 11 ; Тестовых работ – 6; диктанты – 3; Зачетные работы - 3
Особенности класса:
В 8 «А» и «Б» классах обучается 31 учащийся. Качество знаний за курс 7 класса составил 38%. По итогам прошлого года выявлено, что 3 учащихся имеют высокий уровень, 7 учащихся – средний уровень, остальные – низкий уровень обученности. Класс разделен на группы: группа А (сильные учащиеся) В (средние учащиеся) и С ( слабые учащиеся) – все остальные.
Исходя из этого, созданы условия для сохранения и развития здоровья всем учащимся, составлены индивидуальные (траектории) программы работы с детьми с низким уровнем готовности к обучению в школе и пониженной мотивацией, а также подобраны педагогические технологии и методы, описанные ниже.
В программе используются педагогические технологии: игровые технологии; системы развивающего обучения с направленностью на развитие творческих качеств личности; технология уровневой дифференциации обучения на основе обязательных результатов; ИКТ технологии
Методы:
-
методы организации и осуществления учебно-познавательной деятельности: словесный (диалог, рассказ и др.); наглядный (опорные схемы, слайды и др.); практический (упражнения, практические работы, решение задач, моделирование и др.); исследовательский; самостоятельной работы; работы под руководством преподавателя; дидактическая игра;
-
методы стимулирования и мотивации: интереса к учению; долга и ответственности в учении;
-
методы контроля и самоконтроля в обучении: фронтальная устная проверка, индивидуальный устный опрос, письменный контроль (контрольные и практические работы, тестирование, письменный зачет, тесты).
Формы организации деятельности учащихся: классно-урочная, групповая и парная работа, практикумы, экскурсии, индивидуальная работа (работа с учебником, индивидуальные письменные работы и т. д.), практикумы.
Формы текущего, промежуточного и итогового контроля: самостоятельная работа, тестирование, теоретические диктанты, контрольные работы, устные опросы, проверочная работа, зачеты
Требования к уровню подготовки учащихся
Учащиеся должны знать/понимать:
-
значение математической науки для решения задач, возникающих в теории и практике;
-
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа;
должны уметь:
-
выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени;
-
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
-
выполнять основные действия с многочленами и алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные выражения рациональных выражений;
-
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
-
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним системы двух линейных уравнений и несложные нелинейные уравнения;
-
решать линейные и квадратные неравенства с одной переменной и их системы;
-
решать текстовые задачи алгебраическим методом, интерпретировать полученные результат, проводить отбор решений, исходя из формулировки задачи;
-
изображать числа точками на координатной прямой;
-
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
-
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значения аргумента по значению функции, заданной графиком или таблицей;
-
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
-
описывать свойства изученных функций, строить их графики;
-
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать следующие жизненно-практические задачи:
-
самостоятельно приобретать и применять знания в различных ситуациях;
-
работать в группах;
-
аргументировать и отстаивать свою точку зрения;
-
уметь слушать других; извлекать учебную информацию на основе сопоставительного анализа объектов;
-
пользоваться предметным указателем энциклопедий и справочников для нахождения информации.
Тематический план. Формы контроля. Корректировка программы
|
Сроки |
Тема |
Кол-во часов |
Виды контроля |
Корректировка часов программы |
|||||
|
По плану |
По факту |
Сам. р |
тест |
диктант |
Контроль. р |
зачет |
|||
|
|
Повторение |
4 |
|
1 |
1 |
|
1 |
|
|
|
|
Алгебраические дроби |
22 |
|
2 |
1 |
1 |
2 |
|
|
|
|
Функция
|
20 |
|
2 |
1 |
1 |
1 |
1 |
|
|
|
Квадратичная
функция. Функция
|
17 |
|
1 |
|
|
2 |
|
|
|
|
Квадратные уравнения |
20 |
|
2 |
1 |
1 |
2 |
1 |
|
|
|
Неравенства |
19 |
|
2 |
1 |
|
1 |
1 |
|
|
|
Обобщающее повторение |
3 |
|
1 |
1 |
|
1 |
|
|
Тематическое планирование
|
Изучаемый материал |
Кол-во часов |
|
Повторение |
4 |
|
Алгебраические дроби |
22 |
|
Основные понятия |
1 |
|
Основное свойство алгебраической дроби |
2 |
|
Сложение и вычитание алгебраических дробей с одинаковыми знаменателями |
3 |
|
Сложение и вычитание алгебраических дробей с разными знаменателями |
4 |
|
Контрольная работа № 1 |
1 |
|
Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень |
2 |
|
Преобразование рациональных выражений |
3 |
|
Первые представления о решении рациональных уравнений |
2 |
|
Степень с отрицательным целым показателем |
3 |
|
Контрольная работа № 2 |
1 |
|
Функция
|
20 |
|
Рациональные числа |
2 |
|
Понятие квадратного корня из неотрицательного числа |
2 |
|
Иррациональные числа |
1 |
|
Множество действительных чисел |
1 |
|
Функция
|
2 |
|
Свойства квадратных корней |
3 |
|
Преобразование выражений, содержащих операцию извлечения квадратного корня |
5 |
|
Модуль
действительного числа, график функции
|
3 |
|
Контрольная работа № 3 |
1 |
|
Квадратичная
функция. Функция
|
17 |
|
Функция у = кх2, ее свойства и график |
3 |
|
Функция
у = |
2 |
|
Контрольная работа № 4 |
1 |
|
Как построить график функции у = f(x+l), если известен график функции у = f(x). |
2 |
|
. Как построить график функции у = f(x) + m, если известен график функции у = f(x). |
2 |
|
Как построить график функции у = f(x + 1) + m, если известен график функции у = f(x |
2 |
|
Функция у = ах2 + bx + c, ее свойства и график |
3 |
|
Графическое решение квадратных уравнений |
1 |
|
Контрольная работа № 5 |
1 |
|
Квадратные уравнения |
20 |
|
Основные понятия |
2 |
|
Формулы корней квадратных уравнений |
3 |
|
Рациональные уравнения |
3 |
|
Контрольная работа № 6 |
1 |
|
Рациональные уравнения как математические модели реальных ситуаций (текстовые задачи) |
3 |
|
Частные случаи формулы корней квадратного уравнения |
2 |
|
Теорема Виета. Разложение квадратного трехчлена на линейные множители |
2 |
|
Контрольная работа № 7 |
1 |
|
Иррациональные уравнения |
3 |
|
Неравенства |
19 |
|
Свойства числовых неравенств |
3 |
|
Исследование функций на монотонность |
2 |
|
Решение линейных неравенств |
3 |
|
Решение квадратных неравенств |
3 |
|
Контрольная работа № 8 |
1 |
|
Приближенные значения действительных чисел, погрешность приближения, приближение по недостатку и избытку |
2 |
|
Стандартный вид числа |
1 |
|
Обобщающее повторение Итоговая контрольная работа |
3 1 |
|
Всего: |
102 |
Содержание учебного предмета
Действительные числа.
Квадратный корень из числа. Корень третьей степени. Понятие о корне n-ой степени из числа1. Нахождение приближенного значения корня с помощью калькулятора. Запись корней с помощью степени с дробным показателем. Понятие об иррациональном числе. Иррациональность числа. Десятичные приближения иррациональных чисел. Действительные числа как бесконечные десятичные дроби. Сравнение действительных чисел, арифметические действия над ними. Этапы развития представления о числе.
Алгебраические выражения.
Квадратный трехчлен. Выделение полного квадрата в квадратном трехчлене. Теорема Виета. Разложение квадратного трехчлена на линейные множители. Действия с алгебраическими дробями. Рациональные выражения и их преобразования. Свойства квадратных корней и их применение в вычислениях.
Уравнения и неравенства.
Квадратное уравнение: формула корней квадратного уравнения. Решение рациональных уравнений. Неравенство с одной переменной. Решение неравенства. Линейные неравенства с одной переменной. Квадратные неравенства. Числовые неравенства и их свойства.
Числовые функции.
Функции, описывающие прямую и обратную пропорциональную зависимости, их графики. Гипербола. Квадратичная функция, ее график, парабола. Координаты вершины параболы, ось симметрии. Графики функций: корень квадратный, корень кубический, модуль. Параллельный перенос графиков вдоль осей координат и симметрия относительно осей.
Текстовые задачи.
Решение текстовых задач арифметическим способом.
Контрольные измерители
|
№ п/п |
Тема (глава) |
Кол-во часов |
Сроки проведения |
|
1 |
Контрольная работа №1 «Алгебраические дроби» |
1 |
|
|
2 |
Контрольная работа №2 «Алгебраические дроби» |
1 |
|
|
3 |
Контрольная работа №3 «Свойства квадратного корня» |
1 |
|
|
4 |
Контрольная работа № 4 «Квадратичная функция» |
1 |
|
|
5 |
Контрольная
работа № 5 «Функция
|
1 |
|
|
6 |
Контрольная работа № 6 «Квадратные уравнения» |
1 |
|
|
7 |
Контрольная работа № 7 «Квадратные уравнения» |
1 |
|
|
8 |
Контрольная работа № 8 «Неравенства» |
1 |
|
|
|
Итоговая контрольная работа |
1 |
|
|
|
Итого: |
9 |
|
Ресурсное обеспечение
1. Библиотечный фонд
1.1. Нормативные документы: Примерная программа основного общего образо-
вания по математике, Планируемые результаты освоения программы основного
общего образования по математике
1.2. Авторские программы по курсам математики
1.3. Учебники: по алгебре для 7-9 классов, по геометрии для 7-9 классов
1.4. Учебные пособия: рабочие тетради, дидактические материалы, сборники
контрольных работ, самостоятельные работы, тесты.
1.5. Научная, научно-популярная, историческая литература
1.6. Справочные пособия (энциклопедии, словари, справочники по математике и
т.п.)
1.7. Методические пособия для учителя
2. Печатные пособия
2.1.Таблицы по алгебре для 7-9 классов, по геометрии для 7-9 классов
2.2.Портреты выдающихся деятелей математики
3. Информационные средства
3.1. Мультимедийные обучающие программы и электронные учебные издания по
основным разделам курса алгебры
3.2. Электронная база данных для создания тематических и итоговых разноуров-
невых тренировочных и проверочных материалов для организации фронтальной
и индивидуальной работы
4. Экранно-звуковые пособия: видеофильмы по основным темам
, презентации
5. Технические средства обучения
5.1. компьютер
5.2. Мультимедиапроектор
5.3. Интерактивная доска
6. Учебно-практическое и учебно-лабораторное оборудование
6.1. Комплект чертежных инструментов (классных и раздаточных): линейка,
транспортир, угольник (30°, 60°), циркуль
6.2. Комплекты планиметрических и стереометрических тел (демонстрационных
и раздаточных)
Список литературы
Список литературы для учителя
Основная литература:
-
Мордкович А.Г. «Алгебра-8» часть 1 , учебник – М.: Мнемозина, 2010
-
Мордкович А.Г. «Алгебра-8» часть 2, задачник – М.: Мнемозина, 2010
-
Самостоятельные работы. Л.А. Александрова. – М.: Мнемозина. 2007 г.
-
Контрольные работы. Л.А. Александрова.- М.: Мнемозина, 2009 г.
-
Контрольные и самостоятельные работы. М.А. Попов. – М.: Издательство «Экзамен», 2011 г.
Дополнительная литература:
-
Блицопрос. Е.Е. Тульчинская. - М.: Мнемозина, 2009 г.
-
Дидактические материалы. Б.Г. Зив. – М.: Просвещение, 2010 г.
-
Тестовые задания к основным учебникам. В.В. Кочагин. – М.: Эксмо, 2009 г
-
Поурочные разработки
-
Методическое пособие по алгебре для учителя. А.Г. Мордкович. – М.: Мнемозина, 2010 г.
-
Тесты для промежуточных аттестаций. Ф.Ф. Лысенко. – Ростов –на - Дону: Легион – м, 2009 г.
-
Нестандартные уроки 5-10 класс. Л.М. Чернокнижникова. – М.: АРКТИ, 2010 г.
-
Тесты. Е.М. Ключникова, И.В. Комиссарова. – М.: Издательство «Экзамен», 2011 г.
-
Методическое пособие для учителя. А.Г. Мордкович. – М.: Мнемозина, 1997 г.
Интернет ресурсы:
-
http://uchitmatematika. ucos. ru/
-
http:// mikhatoval. edum. ru/
-
http://yroki. net
-
http:// rusedi.ru/
Список литературы для ученика
-
Мордкович А.Г. «Алгебра-8» часть 1 , учебник – М.: Мнемозина, 2010
-
Мордкович А.Г. «Алгебра-8» часть 2, задачник – М.: Мнемозина, 2010
- Международный вебинар «Обучение грамоте старших дошкольников с помощью развивающих игр В. В. Воскобовича: практика реализации ФГОС и ФОП ДО»
- Вебинар «Социально-коммуникативное развитие детей дошкольного возраста в условиях реализации ФОП ДО и обновлённого ФГОС ДО»
- Международный вебинар «Волонтёрство и новые воспитательные практики в школе»
- Психология профессионального образования: общая характеристика
- Международный вебинар «Цель и преимущества использования ТРИЗ-технологии в дошкольном образовании в условиях реализации ФОП ДО»
- Вебинар «Кинезиологические игры и упражнения в развитии психических процессов дошкольников»




