









 Муниципальное
бюджетное общеобразовательное учреждение
Муниципальное
бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 2
|
«Рассмотрено» на заседании ШМО Протокол № ________ от «___»________2014 г. |
«Согласовано» Заместитель директора по УВР МБОУ СОШ № 2 /______________. / ________________2014 г. |
«Утверждено» Директор МБОУ СОШ № 2 /Захарова Н.Ю/. Приказ № _________ от «___»________2014 г. |
РАБОЧАЯ ПРОГРАММА
ПО МАТЕМАТИКЕ
8 класс
На 2014-2015 учебный год
Составители: Андреева М.М.
СОДЕРЖАНИЕ
|
1.Пояснительная записка |
|
|
1.1Статус документа |
|
|
1.2.Общая характеристика учебного предмета |
|
|
1.3. Место предмета в федеральном базисном плане |
|
|
1.4. Требования к уровню подготовки обучающихся в 8 классе |
|
|
2. Содержание рабочей программы Алгебра 8 класс (базовый уровень) |
|
|
3. Содержание рабочей программы Геометрия 8 класс (базовый уровень) |
|
|
4. Календарно- тематическое планирование по алгебре 8 класс (базовый уровень) |
|
|
5. Календарно- тематическое планирование по геометрии 8 класс (базовый уровень) |
|
|
|
|
Пояснительная записка (базовый уровень). Рабочая программа по математике 8 класс.
1.1.Статус документа
Рабочая программа по математике составлена в соответствии с Федеральным компонентом государственного стандарта общего образования, утвержденного Приказом Минобразования РФ от 05.03.2004 г. № 1089 и федеральной примерной программой основного общего образования по математике, с учетом Учебного плана МБОУ СОШ №2 ЗАТО Озерный. Ориентирована на учащихся 8 классов и реализуется на основе следующих документов:
Программы по математике
-
Автор Бурмистрова Т.А. Алгебра. Сборник рабочих программ. 7-9 кл.
год издания 2011 г, издательство М.:Просвещение
-
Автор Бурмистрова Т.А. Программы общеобразовательных учреждений. Геометрия. 7-9 кл. год издания 2008 г, издательство М.:Просвещение
Учебник: Геометрия. 7-9 классы. :/ Атанасян Л.С., Бутузов В.Ф. и др. Москва Просвещение 2006 г.
Учебник: Алгебра 8:/ Колягин Ю. М., Ткачева М.В. и др. Учебник для общеобразовательных учреждений: М. «Просвещение»,2013г
Для обучающихся в 7-11 классах выбрана содержательная линия Ю.М.Колягина, рассчитанная на 5 лет. В восьмом классе реализуется второй год обучения.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса. Рабочая программа выполняет две основные функции:
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Изучение математики в 8 классе направлено на достижение следующих целей:
-
математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Задача образовательного процесса: обеспечить усвоение учащимися обязательного минимума содержания на основе требований государственного образовательного стандарта.
1.2.Общая характеристика учебного предмета.
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Изучение алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия — один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации, и закладываются основы вероятностного мышления.
Цели обучения математики в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека. Алгебра нацелена на формирование математического аппарата для решения задач из математики и смежных предметов (физика, химия, основы информатики и вычислительной техники и др.).
В задачи обучения математики входит:
-
овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования;
-
овладение навыками дедуктивных рассуждений;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, необходимой, в частности, для освоения курса информатики;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и т.д.);
-
воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно технического прогресса;
-
развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.
1.3.Место предмета в федеральном базисном учебном плане
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики на ступени основного общего образования отводится 5 ч в неделю в 8 классах. За счет компонента образовательного учреждения добавлен 1 час.
На преподавание блока алгебры – 4 часа в неделю. Всего 136 час.
На преподавание блока геометрии 2 часа в неделю. Всего 68 часов
Срок реализации рабочей учебной программы – один учебный год.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
-
развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
-
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
-
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
-
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
-
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
-
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
-
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
1.4. Требования к уровню математической подготовки учащихся 8 класса
В результате изучения курса алгебры в 8 классе учащиеся должны
знать/понимать:
• значение математической науки для решения задач, возникающих в теории и на практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
• значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
• универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности; вероятностный характер различных процессов окружающего мира;
должны уметь:
• выполнять арифметические действия, сочетая устные и письменные приемы; находить значение корня натуральной степени, степени с рациональным показателем, используя при необходимости вычислительные устройства, пользоваться оценкой и прикидкой при практических расчетах;
• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
• выполнять основные действия со степенями с целыми показателями, с многочленами и алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
• применять свойства арифметических квадратов корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
• решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные уравнения;
• решать линейные и квадратные неравенства с одной переменой и их системы;
• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
• изображать числа точками на координатной прямой;
• определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значения аргумента по значению функции, заданной графиком или таблицей;
• определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
• описывать свойства изученных функций, строить их графики;
• извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
• решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
• вычислять средние значения результатов измерений;
• находить вероятности случайных событий в простейших случаях;
•
владеть компетенциями: познавательной, коммуникативной, информационной и рефлексивной;
решать следующие жизненно-практические задачи:
• самостоятельно приобретать и применять знания в различных ситуациях;
• работать в группах;
• аргументировать и отстаивать свою точку зрения;
• уметь слушать других; извлекать учебную информацию на основе сопоставительного анализа объектов;
• пользоваться предметным указателем энциклопедий и справочников для нахождения информации;
• самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем.
В результате изучения курса геометрии 8 класса обучающиеся должны:
знать/понимать
-
существо понятия математического доказательства; примеры доказательств;
-
существо понятия алгоритма; примеры алгоритмов;
-
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
-
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
-
как потребности практики привели математическую науку к необходимости расширения понятия числа;
-
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
-
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
-
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
уметь
-
пользоваться языком геометрии для описания предметов окружающего мира;
-
распознавать геометрические фигуры, различать их взаимное расположение;
-
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
-
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
-
в простейших случаях строить сечения и развертки пространственных тел;
-
проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
-
вычислять значения геометрических величин (длин, углов, площадей, объемов), в том числе: для углов от 0 до 180 определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
-
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;
-
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
-
решать простейшие планиметрические задачи в пространстве;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
описания реальных ситуаций на языке геометрии;
-
расчетов, включающих простейшие тригонометрические формулы;
-
решения геометрических задач с использованием тригонометрии
-
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
-
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир)
Для оценки учебных достижений обучающихся используется:
-
текущий контроль в виде проверочных работ и тестов;
-
тематический контроль в виде контрольных работ;
-
итоговый контроль в виде контрольной работы и теста.
Содержание рабочей программы алгебра 8 класс (базовый уровень)
|
№ п/п |
Название темы, раздела |
Кол-во часов |
Содержание изучаемого материала |
Требования к уровню подготовки учащихся |
|
|
Повторение |
4 |
|
|
|
|
Неравенства |
22 |
Положительные и отрицательные числа. Числовые неравенства, их свойства. Сложение и умножение неравенств. Строгие и нестрогие неравенства. Неравенства с одним неизвестным. Системы неравенств с одним неизвестным. Числовые промежутки. |
Уметь решать линейные неравенства с одной переменной и их системы, решать системы линейных неравенств. Знать как используются неравенства; примеры их применения для решения математических и практических задач.
|
|
|
Приближенные вычисления |
10 |
Приближенные значения величин. Погрешность приближения. Оценка погрешности. Округление чисел. Относительная погрешность. Простейшие вычисления на калькуляторе. Стандартный вид числа. Вычисления на калькуляторе степени числа и числа, обратного данному. Последовательное выполнение нескольких операций на калькуляторе. Вычисления на калькуляторе с использованием ячеек памяти. |
Уметь округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений, оценивать погрешность приближения. Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами. Уметь выполнять вычисления с калькулятором, решать различные задачи с помощью калькулятор. Знать понятия приближенных значений величин и погрешности приближения. |
|
|
Квадратные корни |
18 |
Квадратный корень из числа. Арифметический квадратный корень. Понятие об иррациональном числе. Иррациональность числа. Действительные числа. Свойства квадратных корней и их применение в вычислениях. |
Уметь находить в несложных случаях значения корней, применять свойства арифметических квадратных корней для вычисления значений и простейших преобразований числовых выражений, содержащих квадратные корни. Знать понятие арифметического квадратного корня. Уметь применять свойства арифметического квадратного корня при преобразованиях выражений. Уметь выполнять вычисления с калькулятором. Уметь решать различные задачи с помощью калькулятора. Иметь представление о иррациональных и действительных числах. |
|
|
Квадратные уравнения |
30 |
Квадратное уравнение и его корни. Неполные квадратные уравнения. Метод выделения полного квадрата. Решение квадратных уравнений. Разложение квадратного трехчлена на множители. Уравнения, сводящиеся к квадратным. Решение задач с помощью квадратных уравнений. Решение простейших систем, содержащих уравнение второй степени. Уравнение окружности. |
Уметь решать квадратные уравнения и рациональные уравнения, уравнения, сводящиеся к квадратным, простейшие системы, содержащие уравнение второй степени Уметь решать несложные текстовые задачи с помощью уравнений. Понимать, что уравнения – это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики. |
|
|
Квадратичная функция |
18 |
Квадратичная функция, ее график, парабола. Координаты вершины параболы, ось симметрии. Свойства квадратичной функции. Использование графиков функций для решения уравнений и систем. |
Уметь находить значения функции, заданной формулой, таблицей, графиком по ее аргументу. Уметь находить значение аргумента по значению функции, заданной графиком или таблицей. Уметь определять свойства квадратичной функции по ее графику. Уметь применять графические представления при решении уравнений, систем, неравенств. Уметь описывать свойства квадратичной функции. Знать свойства квадратичной функции. Уметь строить график квадратичной функции. Уметь интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы. |
|
|
Квадратные неравенства |
20 |
Квадратное неравенство и его решение. Решение квадратного неравенства с помощью графика квадратичной функции. |
Уметь решать квадратные неравенства. Уметь решать неравенства методом интервалов. |
|
|
Повторение |
14 |
Согласно уровню обученности |
|
|
|
Всего часов |
136 |
|
|
Содержание рабочей программы геометрия 8 класс (базовый уровень)
|
№ п/п |
Название темы, раздела |
Кол-во часов |
Содержание изучаемого материала |
Требования к уровню подготовки учащихся |
|
1. |
Повторение |
2 |
Признаки равенстватреугольников. Соотношения между сторонами и углами треугольника. Свойства равнобедренного треугольника. Признаки и свойства параллельных прямых. |
Знать определения , свойства , признаки и теоремы по данным темам. Уметь применять их при решении задач. |
|
2. |
Четырёхугольники |
14 |
Многоугольник, выпуклый многоугольник. Параллелограмм, прямоугольник, ромб, квадрат, трапеция. Свойства и признаки данных четырехугольников. Осевая, центральная симметрия. |
Знать -определения многоугольника, выпуклого многоугольника; -определения параллелограмма, трапеции, прямоугольника, ромба, квадрата, формулировки их свойств и признаков. Уметь -вывести формулу суммы углов выпуклого многоугольника; -доказывать изученные теоремы и применять их при решении задач. |
|
3. |
Площадь . |
14 |
Измерение площадей многоугольников. Свойства площадей. Площадь прямоугольника, квадрата, параллелограмма, треугольника и трапеции. Теорема об отношении площадей треугольников. Теорема Пифагора и обратная ей. |
Знать -основные свойства площадей; -формулы вычисления площадей прямоугольника, квадрата, параллелограмма, треугольника и трапеции; -теорему об отношении площадей треугольников, имеющих по равному углу; -теорему Пифагора и обратную ей. Уметь -доказать формулы площадей прямоугольника, квадрата, параллелограмма, треугольника и трапеции; -доказать теорему Пифагора и обратную ей; -применять все изученные формулы при решении задач. |
|
4. |
Подобные треугольники. |
19 |
Пропорциональные отрезки. Подобные треугольники. Теорема об отношении площадей подобных треугольников. Свойство биссектрисы треугольника. Три признака подобия треугольников. Теорема о средней линии треугольника. Свойство медиан треугольника. Теоремы о пропорциональных отрезках в прямоугольном треугольнике и деление отрезка в данном отношении. Задачи на построение методом подобия. Синус, косинус и тангенс острого угла прямоугольного треугольника |
Знать -определение пропорциональных отрезков, подобных треугольников; -теорему об отношении площадей подобных треугольников, свойство биссектрисы треугольника; -признаки подобия тругольников; -теоремы о средней линии треугольника, точке пересечения медиан треугольника и пропорциональных отрезках в прямоугольном треугольнике; -определения синуса, косинуса и тангенса острого угла прямоугольного треугольника, значения синуса, косинуса и тангенса для углов 30, 45, 60. Уметь -доказывать теоремы и применять их при решении задач. |
|
5. |
Окружность |
17 |
Окружность. Расположение прямой и окружности. Касательная. Свойства и признак касательной. Градусная мера дуги окружности. Центральный, вписанный углы. Теорема о вписанном угле. Теорема об отрезках пересекающихся хорд. Свойство биссектрисы угла. Серединный перпендикуляр к отрезку. Теорема о серединном перпендикуляре. Теорема о точке пересечения высот треугольника. Вписанная и описанная окружности. Теоремы об окружности, вписанной в треугольник, и об окружности, описанной около треугольника. |
Знать -случаи взаимного расположения прямой и окружности; -определение касательной, свойство и признак касательной; -определения центрального и вписанного углов; -теорему о вписанном угле, следствия из нее; -теорему о произведении отрезков пересекающихся хорд; -теорему о биссектрисе угла и следствии; -теорему о серединном перпендикуляре к отрезку и следствии; -теорему о пересечении высот треугольника; -определения вписанной и описанной окружности; -теоремы об окружности, вписанной в треугольник, и об окружности, описанной около треугольника; -свойства вписанного и описанного четырех угольника. Уметь - доказывать теоремы и применять их при решении задач. |
|
6. |
Итоговое повторение курса геометрии 8 класса. |
2 |
Согласно уровню обученности |
|
|
|
Всего: |
68 |
|
|
Муниципальное бюджетное общеобразовательное учреждение –
средняя общеобразовательная школа № 2
ЗАТО Озерный Тверской области
|
|
СОГЛАСОВАНО Заместитель директора МБОУ СОШ № 2 ___________ _______________ «______»_____________20___г. |
Календарно-тематическое планирование
по математике в 8 классе
учителя Андреевой М.М.
на 2014 -2015 учебный год
Пояснительная записка к календарно-тематическому планированию
Планирование составлено на основе Программы по математике
Автор Бурмистрова Т.А. Алгебра. Сборник рабочих программ. 7-9 кл.
год издания 2011 г, издательство М.:Просвещение
Автор Бурмистрова Т.А. Программы общеобразовательных учреждений. Геометрия. 7-9 кл. год издания 2008 г, издательство М.:Просвещение
Учебник: Алгебра 8 кл. Колягин Ю. М., Ткачева М.В. и др.
М. «Просвещение»,2013г
Учебник: Геометрия. 7-9 классы. :/ Атанасян Л.С., Бутузов В.Ф. и др. Москва Просвещение 2006 г.
Часов в неделю 6 ч.
По программе за год 204 ч.
Учебно-тематический план
|
Название темы, раздела |
Кол-во часов |
|
Алгебра |
|
|
Повторение |
4 |
|
Неравенства |
22 |
|
Приближенные вычисления |
10 |
|
Квадратные корни |
18 |
|
Квадратные уравнения |
30 |
|
Квадратичная функция |
18 |
|
Квадратные неравенства |
20 |
|
Повторение |
14 |
|
Всего: |
136 |
|
Геометрия |
|
|
|
|
|
Повторение |
2 |
|
Четырёхугольники |
14 |
|
Площадь. |
14 |
|
Подобные треугольники. |
19 |
|
Окружность |
17 |
|
Итоговое повторение курса геометрии 8 класса. |
2 |
|
Всего: |
68 |
Контрольные работы по алгебре
|
Тема контрольной работы |
Дата проведения контрольной работы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Календарно тематическое планирование по алгебре 8 класс (базовый уровень)
|
№ урока |
Содержание учебного материала |
Количество часов |
План. дата |
Факт. дата |
План. дата |
Факт. дата |
|
8а |
8а |
8б |
8б |
|||
|
1-4 |
Повторение |
4 |
|
|
|
|
|
|
1. Числовые неравенства. |
22 |
|
|
|
|
|
|
Положительные и отрицательные числа. |
1 |
|
|
|
|
|
|
Положительные и отрицательные числа |
1 |
|
|
|
|
|
|
Числовые неравенства. |
1 |
|
|
|
|
|
|
Основные свойства числовых неравенств. |
1 |
|
|
|
|
|
|
Основные свойства числовых неравенств |
1 |
|
|
|
|
|
|
Сложение и умножение числовых неравенств. |
1 |
|
|
|
|
|
|
Строгие и нестрогие неравенства. |
1 |
|
|
|
|
|
|
Неравенства с одним неизвестным. |
1 |
|
|
|
|
|
|
Решение неравенств. |
1 |
|
|
|
|
|
|
Решение неравенств. |
1 |
|
|
|
|
|
|
Геометрическая иллюстрация решений. |
1 |
|
|
|
|
|
|
Система неравенств с одним неизвестным. Числовые промежутки. |
1 |
|
|
|
|
|
|
Решение систем неравенств. |
1 |
|
|
|
|
|
|
Решение систем неравенств. |
1 |
|
|
|
|
|
|
Решение систем неравенств. |
1 |
|
|
|
|
|
|
Решение задач с помощью систем неравенств. |
1 |
|
|
|
|
|
|
Понятие модуля числа.. |
1 |
|
|
|
|
|
|
Уравнения и неравенства содержащие модуль |
1 |
|
|
|
|
|
|
Решение уравнений и неравенств содержащих модуль |
1 |
|
|
|
|
|
|
Оощающий урок по теме: «Числовые неравенства». |
1 |
|
|
|
|
|
|
Контрольная работа №1 по теме: «Числовые неравенства». |
1 |
|
|
|
|
|
|
Анализ контрольной работы№1. |
1 |
|
|
|
|
|
|
2. Приближенные вычисления. |
10 |
|
|
|
|
|
|
Приближенные значения величин. Погрешность приближения. |
1 |
|
|
|
|
|
|
Оценка погрешности. |
1 |
|
|
|
|
|
|
Округление чисел. |
1 |
|
|
|
|
|
|
Относительная погрешность. Абсолютная погрешность.. |
1 |
|
|
|
|
|
|
Практические приемы приближенных вычислений |
1 |
|
|
|
|
|
|
Простейшие вычисления на микрокалькуляторе |
1 |
|
|
|
|
|
|
Действия над числами, записанными в стандартном виде. |
1 |
|
|
|
|
|
|
Вычисления на МК степени числа, обратного данному |
1 |
|
|
|
|
|
|
Последовательное выполнение операций на микрокалькуляторе |
1 |
|
|
|
|
|
|
Контрольная работа №2 по теме «Приближенные вычисления» |
1 |
|
|
|
|
|
|
3. Квадратные корни |
18 |
|
|
|
|
|
|
Арифметический квадратный корень. |
1 |
|
|
|
|
|
|
Арифметический квадратный корень. |
1 |
|
|
|
|
|
|
Действительные числа. |
1 |
|
|
|
|
|
|
Действительные числа. |
1 |
|
|
|
|
|
|
Квадратный корень из степени. |
1 |
|
|
|
|
|
|
Квадратный корень из степени. |
1 |
|
|
|
|
|
|
Квадратный корень из степени. |
1 |
|
|
|
|
|
|
Квадратный корень из произведения. |
1 |
|
|
|
|
|
|
Квадратный корень из произведения. |
1 |
|
|
|
|
|
|
Квадратный корень из произведения. |
1 |
|
|
|
|
|
|
Квадратный корень из дроби. |
1 |
|
|
|
|
|
|
Квадратный корень из дроби. |
1 |
|
|
|
|
|
|
Квадратный корень из дроби. |
1 |
|
|
|
|
|
|
Преобразование выражений, содержащих квадратные корни. |
1 |
|
|
|
|
|
|
Преобразование выражений, содержащих квадратные корни. |
1 |
|
|
|
|
|
|
Обобщающий урок по теме «Квадратные корни» |
1 |
|
|
|
|
|
|
Контрольная работа №3 по теме:« Квадратные корни» |
1 |
|
|
|
|
|
|
Анализ контрольной работы. |
1 |
|
|
|
|
|
|
4. Квадратные уравнения |
30 |
|
|
|
|
|
|
Квадратные уравнения и его корни. |
1 |
|
|
|
|
|
|
Квадратные уравнения и его корни. |
1 |
|
|
|
|
|
|
Неполные квадратные уравнения. |
1 |
|
|
|
|
|
|
Неполные квадратные уравнения. |
1 |
|
|
|
|
|
|
Метод выделения полного квадрата. |
1 |
|
|
|
|
|
|
Решение квадратных уравнений. |
1 |
|
|
|
|
|
|
Решение квадратных уравнений. |
1 |
|
|
|
|
|
|
Решение квадратных уравнений. |
1 |
|
|
|
|
|
|
Приведенное квадратное уравнение. |
1 |
|
|
|
|
|
|
Теорема Виета. |
1 |
|
|
|
|
|
|
Разложение квадратного трехчлена на множители. |
1 |
|
|
|
|
|
|
Уравнения, сводящиеся к квадратным. |
1 |
|
|
|
|
|
|
Биквадратные уравнения. |
1 |
|
|
|
|
|
|
Дробно-рациональные уравнения |
1 |
|
|
|
|
|
|
Решение задач с помощью квадратных уравнений. |
1 |
|
|
|
|
|
|
Решение задач с помощью квадратных уравнений. |
1 |
|
|
|
|
|
|
Решение задач с помощью квадратных уравнений. |
1 |
|
|
|
|
|
|
Решение задач с помощью квадратных уравнений. |
1 |
|
|
|
|
|
|
Решение простейших систем, содержащих уравнение второй степени (метод подстановки) |
1 |
|
|
|
|
|
|
Решение простейших систем, содержащих уравнение второй степени (метод подстановки) |
1 |
|
|
|
|
|
|
Решение простейших систем, содержащих уравнение второй степени (метод сложения) |
1 |
|
|
|
|
|
|
Решение простейших систем, содержащих уравнение второй степени (метод сложения) |
1 |
|
|
|
|
|
|
Различные способы решения систем уравнений |
1 |
|
|
|
|
|
|
Различные способы решения систем уравнений |
1 |
|
|
|
|
|
|
Решение задач с помощью систем уравнений |
1 |
|
|
|
|
|
|
Решение задач с помощью систем уравнений |
1 |
|
|
|
|
|
|
Обобщающий урок по теме «Квадратные уравнения» |
1 |
|
|
|
|
|
|
Обобщающий урок по теме «Квадратные уравнения» |
1 |
|
|
|
|
|
|
Контрольная работа №4 по теме: « Квадратные уравнения» |
1 |
|
|
|
|
|
|
Анализ контрольной работы |
1 |
|
|
|
|
|
|
5. Квадратичная функция |
18 |
|
|
|
|
|
|
Определение квадратичной функции |
1 |
|
|
|
|
|
|
Определение квадратичной функции |
1 |
|
|
|
|
|
|
Функция
|
1 |
|
|
|
|
|
|
Функция
|
1 |
|
|
|
|
|
|
Функция
|
1 |
|
|
|
|
|
|
Функция
|
1 |
|
|
|
|
|
|
Функция
|
1 |
|
|
|
|
|
|
Функция
|
1 |
|
|
|
|
|
|
Свойства квадратичной функции. |
|
|
|
|
|
|
|
Схема исследования квадратичной функции и построение её графика. |
1 |
|
|
|
|
|
|
Построение графика квадратичной функции. |
1 |
|
|
|
|
|
|
Построение графика квадратичной функции. |
1 |
|
|
|
|
|
|
Построение графика квадратичной функции. |
1 |
|
|
|
|
|
|
Построение графика квадратичной функции. |
1 |
|
|
|
|
|
|
Решение упражнений по теме: « Квадратичная функция». |
1 |
|
|
|
|
|
|
Обобщающий урок по теме «Квадратичная функция» |
1 |
|
|
|
|
|
|
Контрольная работа №5 по теме: « Квадратичная функция». |
1 |
|
|
|
|
|
|
Анализ контрольной работы |
1 |
|
|
|
|
|
|
Квадратные неравенства |
20 |
|
|
|
|
|
|
Квадратное неравенство и его решение. |
1 |
|
|
|
|
|
|
Квадратное неравенство и его решение. |
1 |
|
|
|
|
|
|
Решение квадратных неравенств |
1 |
|
|
|
|
|
|
Алгоритм решение квадратных неравенств с помощью графика квадратичной функции. |
1 |
|
|
|
|
|
|
Решение квадратных неравенств с помощью графика квадратичной функции. |
1 |
|
|
|
|
|
|
Решение квадратных неравенств с помощью графика квадратичной функции. |
1 |
|
|
|
|
|
|
Решение квадратных неравенств с помощью графика квадратичной функции. |
1 |
|
|
|
|
|
|
Метод интервалов. |
1 |
|
|
|
|
|
|
Решение неравенств методом интервалов |
1 |
|
|
|
|
|
|
Решение неравенств методом интервалов |
1 |
|
|
|
|
|
|
Решение неравенств методом интервалов |
1 |
|
|
|
|
|
|
Решение неравенств методом интервалов |
1 |
|
|
|
|
|
|
Решение неравенств методом интервалов |
1 |
|
|
|
|
|
|
Исследование квадратного трехчлена. |
1 |
|
|
|
|
|
|
Исследование квадратного трехчлена. |
1 |
|
|
|
|
|
|
Решение упражнений по теме: « Квадратные неравенства». |
1 |
|
|
|
|
|
|
Решение упражнений по теме: « Квадратные неравенства». |
1 |
|
|
|
|
|
|
Обобщающий урок по теме «Квадратные неравенства» |
1 |
|
|
|
|
|
|
Контрольная работа №6 по теме: «Квадратные неравенства». |
1 |
|
|
|
|
|
|
Анализ контрольной работы |
1 |
|
|
|
|
|
|
Итоговое повторение |
14 |
|
|
|
|
|
|
Решение линейных неравенств |
1 |
|
|
|
|
|
|
Решение линейных неравенств |
1 |
|
|
|
|
|
|
Решение систем линейных неравенств |
1 |
|
|
|
|
|
|
Квадратный корень. Преобразование выражений, содержащих квадратные корни. |
1 |
|
|
|
|
|
|
Преобразование выражений, содержащих квадратные корни. |
1 |
|
|
|
|
|
|
Решение квадратных уравнений |
1 |
|
|
|
|
|
|
Решение квадратных уравнений |
1 |
|
|
|
|
|
|
Решение систем квадратных уравнений |
1 |
|
|
|
|
|
|
Решение квадратных неравенств |
1 |
|
|
|
|
|
|
Решение квадратных неравенств |
1 |
|
|
|
|
|
|
Решение квадратных неравенств |
1 |
|
|
|
|
|
|
Решение упражнений по теме: « Квадратичная функция». |
1 |
|
|
|
|
|
|
Решение упражнений по теме: « Квадратичная функция». |
1 |
|
|
|
|
|
|
Итоговая контрольная работа |
1 |
|
|
|
|
|
|
Всего: |
136 |
|
|
|
|
Контрольные работы по геометрии
|
Тема контрольной работы |
Дата проведения контрольной работы |
|
«Четырехугольники». |
|
|
«Теорема Пифагора». |
|
|
«Подобные треугольники». |
|
|
«Применение подобия к решению задач». |
|
|
«Окружность». |
|
Календарно – тематическое планирование по геометрии 8 класс (базовый уровень)
|
№ урока |
Содержание учебного материала |
Кол-во часов |
План. дата |
Факт.дата |
План. дата |
Факт.дата |
|
8а |
8а |
8б |
8б |
|||
|
|
Повторение |
2 |
|
|
|
|
|
|
Признаки равенства треугольников. Равнобедренный треугольник. |
1 |
|
|
|
|
|
|
Параллельные прямые. Сумма углов треугольников. |
1 |
|
|
|
|
|
|
Глава 5. Четырёхугольники |
14 |
|
|
|
|
|
|
Многоугольники. |
1 |
|
|
|
|
|
|
Решение задач по теме: «Многоугольники». |
1 |
|
|
|
|
|
|
Параллелограмм. Свойства параллелограмма. |
1 |
|
|
|
|
|
|
Признаки параллелограмма. |
1 |
|
|
|
|
|
|
Решение задач по теме: «Параллелограмм». |
1 |
|
|
|
|
|
|
Трапеция. |
1 |
|
|
|
|
|
|
Теорема Фалеса. |
1 |
|
|
|
|
|
|
Задачи на построение. |
1 |
|
|
|
|
|
|
Прямоугольник. |
1 |
|
|
|
|
|
|
Ромб и квадрат. |
1 |
|
|
|
|
|
|
Решение задач |
1 |
|
|
|
|
|
|
Осевая и центральные симметрии. |
1 |
|
|
|
|
|
|
Решение задач по теме: «Четырехугольники». |
1 |
|
|
|
|
|
|
Контрольная работа №1 по теме: «Четырехугольники». |
1 |
|
|
|
|
|
|
Глава 6. Площадь . |
14 |
|
|
|
|
|
|
Понятие площади многоугольника. Площадь квадрата. |
1 |
|
|
|
|
|
|
Площадь прямоугольника. |
1 |
|
|
|
|
|
|
Площадь параллелограмма. |
1 |
|
|
|
|
|
|
Площадь треугольника. |
1 |
|
|
|
|
|
|
Площадь треугольника. |
1 |
|
|
|
|
|
|
Площадь трапеции. |
1 |
|
|
|
|
|
|
Решение задач на вычисление площадей фигур. |
1 |
|
|
|
|
|
|
Решение задач на нахождение площади. |
1 |
|
|
|
|
|
|
Теорема Пифагора. |
1 |
|
|
|
|
|
|
Теорема, обратная теореме Пифагора. |
1 |
|
|
|
|
|
|
Решение задач по теме «Теорема Пифагора». |
1 |
|
|
|
|
|
|
Решение задач: «Площади». |
1 |
|
|
|
|
|
|
Решение задач. |
|
|
|
|
|
|
|
Контрольная работа №2 по теме «Теорема Пифагора». |
1 |
|
|
|
|
|
|
Глава 7. Подобные треугольники. |
20 |
|
|
|
|
|
|
Пропорциональные отрезки. Определение подобных треугольников. |
1 |
|
|
|
|
|
|
Отношение площадей подобных треугольников. |
1 |
|
|
|
|
|
|
Первый признак подобия треугольников. |
1 |
|
|
|
|
|
|
Решение задач на применение первого признака подобия треугольников. |
1 |
|
|
|
|
|
|
Второй и третий признаки подобия треугольников. |
1 |
|
|
|
|
|
|
Решение задач на применение признаков подобия треугольников. |
1 |
|
|
|
|
|
|
Решение задач на применение признаков подобия треугольников. |
1 |
|
|
|
|
|
|
Контрольная работа №3 по теме «Подобные треугольники». |
1 |
|
|
|
1 |
|
|
Средняя линия треугольника. |
1 |
|
|
|
|
|
|
Средняя линия треугольника.Свойство медиан в треугольнике. |
1 |
|
|
|
|
|
|
Пропорциональные отрезки. |
1 |
|
|
|
|
|
|
Пропорциональные отрезки в прямоугольном треугольнике. |
1 |
|
|
|
|
|
|
Измерительные работы на местности. |
1 |
|
|
|
|
|
|
Задачи на построение методом подобия. |
1 |
|
|
|
|
|
|
Решение задач на построение методом подобных треугольников. |
1 |
|
|
|
|
|
|
Синус, косинус и тангенс острого угла прямоугольного треугольника. |
1 |
|
|
|
|
|
|
Значения синуса, косинуса и тангенса для углов 30°, 45° и 60°. |
1 |
|
|
|
|
|
|
Соотношения между сторонами и углами прямоугольного треугольника. Решение задач |
1 |
|
|
|
|
|
|
Решение задач. |
1 |
|
|
|
|
|
|
Контрольная работа №4 по теме: «Применение подобия к решению задач». |
1 |
|
|
|
1 |
|
|
Глава 8. Окружность |
16 |
|
|
|
|
|
|
Взаимное расположение прямой и окружности |
1 |
|
|
|
|
|
|
Касательная к окружности. |
1 |
|
|
|
|
|
|
Касательная к окружности. Решение задач. |
1 |
|
|
|
|
|
|
Градусная мера дуги окружности |
1 |
|
|
|
|
|
|
Теорема о вписанном угле. |
1 |
|
|
|
|
|
|
Теорема об отрезках пересекающихся хорд. |
1 |
|
|
|
|
|
|
Решение задач по теме «Центральные и вписанные углы». |
1 |
|
|
|
|
|
|
Свойство биссектрисы угла. |
1 |
|
|
|
|
|
|
Серединный перпендикуляр. |
1 |
|
|
|
|
|
|
Теорема о точке пересечения высот треугольника |
1 |
|
|
|
|
|
|
Вписанная окружность. |
1 |
|
|
|
|
|
|
Свойство описанного четырехугольника. |
1 |
|
|
|
|
|
|
Описанная окружность. |
1 |
|
|
|
|
|
|
Свойство вписанного четырехугольника. |
1 |
|
|
|
|
|
|
Решение задач по теме «Окружность». |
1 |
|
|
|
|
|
|
Контрольная работа №5 по теме «Окружность». |
1 |
|
|
|
1 |
|
|
Итоговое повторение курса геометрии 8 класса. |
2 |
|
|
|
|
|
|
Анализ контрольной работы.Повторение по темам «Четырёхугольники», «Площадь». |
1 |
|
|
|
|
|
|
Повторение по темам «Подобные треугольники», «Окружность». |
1 |
|
|
|
|
|
|
Всего: |
68 |
|
|
|
5 |
Контрольно-измерительные материалы по алгебре.
Контрольная работа №1 «Неравенства»
Вариант1.
1. Пусть а < 0, b > 0. Сравните с нулем значение выражения:
а) а5b6;
б)
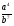 ;
в) а(3b
– a);
г)
;
в) а(3b
– a);
г)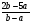 .
.
2. Докажите, что при любых значениях b верно неравенство:
а) (b-3)2 > b(b-6); б) b2 +10 ≥ 2(4b-3).
3. Известно, что a < b. Сравните:
а)15a и 15b; б) -6,3а и -6,3b; в) -8b и -8а.
4. Решите уравнение:
а) (3х-1)(2+5х) =
0; б)
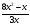 =0.
=0.
Вариант 2.
1. Пусть х < 0, y < 0. Сравните с нулем значение выражения:
а) x3y8;
б)
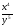 ;
в) 3y(2x+y);
г)
;
в) 3y(2x+y);
г)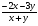 .
.
2. Докажите, что при любых значениях a верно неравенство:
а) (a-5)2 > a(a -10); б) a2 +12 ≥ 4(2a -1).
3. Известно, что с > d. Сравните:
а) 3,4c и 3,4d; б) -c и -d; в) -6,5d и -6,5c.
4. Решите уравнение:
а) (5х-3)(6х+2) =
0; б)
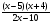 =0.
=0.
Контрольная работа №2«Неравенства и системы неравенств»
Вариант1.
1. Решите неравенство:
а)
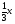 >3;
б) 1 – 6х ≤0 ; в) 6(3,4 +х) – 4,2 > х+1.
>3;
б) 1 – 6х ≤0 ; в) 6(3,4 +х) – 4,2 > х+1.
2. При каких
b
значение дроби
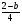 больше
соответствующего значения дроби
больше
соответствующего значения дроби
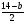 ?
?
3. Решите систему неравенств:
а) { 5х-8< 0, б ) { 7 - 3х< 1
3х+4>0; 1,8 - х< 1,9.
4. Решите уравнение:
а) │2х+3│= 7; б) │1 – 3х│=37.
5. Решите неравенство:
а) │2х - 1│< 3; б) │6х+2│≥ 5.
Вариант 2.
1. Решите неравенство:
а)
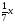 <1; б) 3 – 5х ≥0 ; в) 5(х – 1,8) – 4,6 > 3х –
1,6.
<1; б) 3 – 5х ≥0 ; в) 5(х – 1,8) – 4,6 > 3х –
1,6.
2. При каких
b
значение дроби
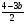 меньше
соответствующего значения двучлена
12+b?
меньше
соответствующего значения двучлена
12+b?
3. Решите систему неравенств:
а) { 2х+9 >0, б ) { 4 - 6х< 1
9х-1< 0; 3,6+ х> 3,8.
4. Решите уравнение:
а) │5х+1│= 6; б) │3 – 7х│=19.
5. Решите неравенство:
а) │10х + 1│> 21; б) │2 - 6х│≤ 4.
Контрольная работа №3 «Приближенные вычисления»
Вариант 1.
-
Округлите число 2,53 до десятых и найдите абсолютную и относительную погрешность округления.
-
Запишите число в стандартном виде:
а) 48,16; б) 0,0184.
3. Выполните действия (ответ дайте с точностью до 0.01)
а) 4,12+26,1872; в) 37,12 – 19,268;
б) 3,2· 21,34; г) 9,162: 3,25.
4. Запишите программу вычисления на микрокалькуляторе и найдите значение выражения: (1,72· 6,3 +8,2):5,42 – (0,16)3.
Вариант 2.
-
Округлите число 0,38 до десятых и найдите абсолютную и относительную погрешность округления.
-
Запишите число в стандартном виде:
а) 159,6; б) 0,00043.
3. Выполните действия (ответ дайте с точностью до 0.01)
а) 12,784+5,36; в) 47,184 – 5,26;
б) 4,5· 16,64; г) 16,45: 2,51.
4. Запишите программу вычисления на микрокалькуляторе и найдите значение выражения: (2,37+1,56 : 3,16)· 4,81 – (3,21)5.
Контрольная работа№4 «Квадратные корни» 8кл
Вариант №1.
-
Вычислите:

а) 6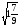 - 4; б)
- 4; б)
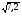
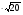 ;
в)
;
в)
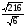 ;
г)
;
г)
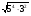 .
.
-
Упростите выражение:
а) 4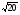 -
-
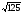 ; б) ( 3
; б) ( 3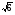 +
+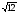 )
)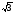 ;
в) (5 -
;
в) (5 -
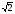 )2.
)2.
-
Внесите множитель под знак корня:
а) 12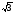 ;
б) -9
;
б) -9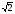 .
.
4. Упростите
выражение
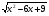 и найдите его значение
и найдите его значение
при х=2,6.
5. Сократите дробь:
а)
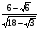 ; б)
; б)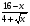 .
.
Вариант №2.
-
Вычислите:

а) 3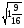 - 1; б)
- 1; б)
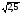
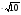 ;
в)
;
в)
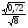 ;
г)
;
г)
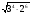 .
.
-
Упростите выражение:
а) 5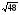 - 2
- 2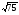 ; б) ( 3
; б) ( 3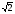 +
+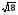 )
)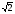 ;
в) (4 -
;
в) (4 -
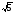 )2.
)2.
-
Внесите множитель под знак корня:
а) 15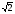 ;
б) -8
;
б) -8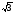 .
.
4. Упростите
выражение
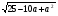 и найдите его значение
и найдите его значение
при а = 3,7.
5. Сократите дробь:
а)
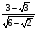 ; б)
; б)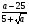 .
.
Контрольная работа №5 «Квадратные уравнения» 8кл
Вариант 1.
1.Решите
уравнение:а)14х2
-
9х = 0; б)16х2
=
49; в)2х2
-
11х + 12 = 0; г) х2
-
36х + 324 = 0; д) 2х2
+х
+ 16 = 0; е)
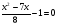 .
.
2. Решите биквадратное уравнение: х4 - 13х + 36 = 0.
3. Сократите
дробь
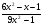
4. Один из корней уравнения х2 + рx + 45 = 0 равен 5. Найдите другой корень и коэффициент р.
Вариант 2.
1. Решите уравнение: а) 6х – 5х2 = 0; б) 25х2 = 1; в) 4х2 - 7х -2= 0;
г) 4х2
+20х
+ 25 = 0; д) 3х2
+2х
+ 1 = ; е)
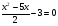 .
.
2. Решите биквадратное уравнение: х4 - 29х +100= 0.
3. Сократите
дробь
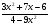
4. Один из корней уравнения х2- 26x + q = 0 равен 12. Найдите другой корень и слагаемое q.
Контрольная работа №6 «Квадратные уравнения и системы уравнений»
Вариант 1.
1. Решите
уравнение:
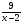 -
-
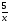 = 2.
= 2.
2. Решите систему уравнений: { х – 2у = 4
ху = 6.
3. Расстояние из А в В длиной 60 км мотоциклист проехал по шоссе, а обратно возвратился по проселочной дороге, короче первой на 5 км, уменьшив скорость на 10 км/ч. С какой скоростью ехал мотоциклист из А в В, если известно, что на путь по проселочной дороге он затратил на 6 мин больше, чем на путь по шоссе?
Вариант 2.
1. Решите
уравнение:
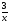 -
-
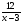 = 1.
= 1.
2. Решите
систему уравнений: { 3х –у = 1,
ху =10.
3. Моторная лодка прошла 28 км против течения реки и 16 км по течению, затратив на весь путь 3часа. Какова скорость моторной лодки в стоячей воде, если известно, что скорость течения реки равна 1км/ч.
Контрольная работа №7 «Квадратичная функция»
Вариант1.
-
При каких значениях х функция у= -2х2+5х+3 принимает значение, равное -4?
-
Постройте график функции у= х2 - 2х – 8. Найдите с помощью графика:
а) значение у при х=-1,5;
б) значения х, при которых у=3;
в) значения х, при которых у >0;
г) промежуток, в котором функция убывает.
3. Не выполняя построения графика функции у = -5х2+6х, найдите ее наибольшее или наименьшее значение.
Вариант2.
-
При каких значениях х функция у= -3х2+7х+1 принимает значение, равное -5?
Постройте график функции у= х2 +4х – 2. Найдите с помощью графика:
а) значение у при х =1,5;
б) значения х, при которых у =4;
в) значения х, при которых у <0;
г) промежуток, в котором функция убывает.
3. Не выполняя построения графика функции у = 7х2 - 4х, найдите ее наибольшее или наименьшее значение.
Контрольная работа №8 «Неравенства»
Вариант1.
-
Решите неравенство:
а) 4х2 – 4х - 15<0; б) х2 - 81>0; в) х2< 1,7х;
г) х(х+3)-6< 3(х+1).
2. Решите неравенство методом интервалов:
а) (х+8)(х –
3) >0; б)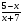 >0; в) х3-
64х<0;
>0; в) х3-
64х<0;
3. При каких значениях х имеет смысл выражение
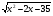 ?
?
Вариант2.
-
Решите неравенство:
а) 2х2 +5х - 12>0; б) х2 - 64< 0; в) х2 > 2,3х;
г) х(х- 5) – 29 > 5(4 - х).
2. Решите неравенство методом интервалов:
а) (х -
4)(х+7) <0; б)
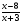 >0; в) х3-
49х >0;
>0; в) х3-
49х >0;
3. При каких значениях х имеет смысл выражение
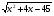 ?
?
КОНТРОЛЬНО- ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ ПО ГЕОМЕТРИИ.
Контрольная работа по геометрии №1 по теме « Четырехугольники» 8кл.
Вариант1.
1.Диагонали прямоугольника АВСD пересекаются в точке О.Найдите угол между диагоналями, если ےАВО = 30˚.
2.В параллелограмме КМNP проведена биссектриса угла МКP,которая пересекает сторону МN в точке Е. а) Докажите, что треугольник КМЕ - равнобедренный. б)Найдите сторону КР, если МЕ=10см, а периметр параллелограмма равен 52см.
Вариант2.
1.Диагонали ромба КМNP пересекаются в точке О.Найдите углы треугольника КОМ, если ےМNP = 80˚.
2. На стороне ВС параллелограмма АВСD взята точка М так, что АВ=ВМ.
а) Докажите,
что высота АМ - биссектриса угла ВАД.
б)Найдите периметр параллелограмма,
если СD = 8см, а СМ = 4см.
Контрольная работа №3 по теме «Признаки подобия треугольников»
Вариант I.
1. На рисунке АВ || CD. а) Докажите, что АО : ОС = ВО : ОD. б) Найдите АВ, если ОD=15см, ОВ=9 см, CD=25 см.
А В
О
D C
2. Найдите отношение площадей треугольников АВС и KMN, если АВ=8см, ВС= 12см, АС= 16см и КМ=10 см, MN=15 см, NK=20 см.
Вариант II.
1. На рисунке MN || АC. а) Докажите, что АВ : ВN = СВ : ВМ. б) Найдите MN, если АM =6см, ВM=8 см, АC=21см.
B
M N
A C
2. Найдите отношение площадей треугольников PQR и ABC, если PQ=16см, QR= 20см, PR= 28 см и АВ=12 см, ВС=15 см, АС=21 см
Контрольная работа по геометрии № 4 по теме « Соотношение между сторонами и углами прямоугольного треугольника» 8кл.
Вариант1.
1. В прямоугольном треугольнике АВС ےА=90˚, АВ=20 см, высота АD равна 12 см. Найдите АС и cos C.
2. Диагональ ВD параллелограмма АВСD перпендикулярна к стороне АD. Найдите площадь параллелограмма АВСD, если АВ=12 см, ےА=41˚.
Вариант2.
1. В прямоугольном треугольнике АВС высота ВD равна 24см и отсекает от
гипотенузы АС отрезок DС, равный 18см. Найдите АВ и cos А.
2. Диагональ АС прямоугольника АВСD равна 3см и составляет со стороной АD угол в 37˚. Найдите площадь прямоугольника АВСD.
Контрольная работа по геометрии № 5 по теме « Окружность» 8кл.
Вариант1.
1.Через точку А окружности проведены диаметр АС и две хорды АВ и АD, равные радиусу этой окружности. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СD, АD.
2. Основание равнобедренного треугольника равно 18см, а боковая сторона равна 15см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Вариант2.
1. Отрезок ВD - диаметр окружности с центром О. Хорда АС делит пополам радиус ОВ и перпендикулярна к нему. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СD, АD.
2. Высота, проведенная к основанию равнобедренного треугольника, равна 9см, а само основание равно 24см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
- Международный вебинар «Обучение грамоте старших дошкольников с помощью развивающих игр В. В. Воскобовича: практика реализации ФГОС и ФОП ДО»
- Международный вебинар «Волонтёрство и новые воспитательные практики в школе»
- Контрольно-оценочная деятельность учителя начальных классов в условиях реализации ФГОС НОО
- Методы и приемы формирования и оценки УУД младших школьников в соответствии с ФГОС НОО
- Проектирование современного урока математики: реализация требований ФГОС
- Организация исследовательской и проектной деятельности обучающихся начальной школы как основное требование ФГОС НОО





 .
.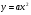 .
.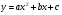 .
.