Изучение процентов

«ИЗУЧЕНИЕ ПРОЦЕНТОВ»

Автор:

Кобышева Генриетта Ильинична,

учитель математики

Жутовской второй средней школы

с. Жутово-2 Октябрьского района

Волгоградской области

2014 год.

Задачи на проценты — трудная для учащихся тема.

Применяя технологию укрупнения дидактических единиц (УДЕ) П. Эрдниева, можно изучить три вида задач на проценты одновременно. Это экономит время примерно на 20% и дает качество знаний примерно на 65-70%.

В программе предусмотрено изучать «Проценты», потом «Пропорции». У учащегося возникают трудности:1) ему надо запомнить название типа задач;

2) знать правила нахождения % от числа, числа по его % и находить % отношения.

По УДЕ всё — в одной главе: «Отношение. Пропорция. Процент», причем решение любого вида задач на % сводится к единообразному алгоритму составления пропорции, основанному на следующей цепочке операций:

1. Напиши условие задач

2. В левом верхнем углу напиши 100%

3. Напиши % под %

4. Заполни таблицу числами, искомую величину обозначь буквой.

5. Составь уравнение (пропорцию) и реши его (найди неизвестный член пропорции).

100% -

% -

100% -

2 % -

100% - 50р.

2% - Хр.

100 = 50

2 Х

100*Х=2*50

Х=2*50

100

Х=1.

Фрагменты из урока

I. Изучение нового материала

Зная, что в классе 30 учащихся и девочек 18, составь задачу.

Запишем схему задачи: 30,18,

Составь условие задачи.

В 6 классе 30 учащихся. Девочек 18

Сколько % от числа всех учащихся

составляют девочки?

Тип задачи	Нахождение % отношения	Нахождение числа по %	Нахождение % от числа
Схема задачи	30,18,	,18, 60%	30, ,60%
Условие задачи	В классе 30 учащихся. Девочек — 18. Сколько % от всех учащихся составляют девочки?	В классе 18 девочек, что составляет 60% всех учащихся класса. Сколько учащихся в классе?	В классе 30 учащихся. Девочки составляют 60% от всех учащихся класса. Сколько девочек в классе?
Напишем в левом верхнем углу 100%, а рядом напишем соответствующее число	100% - 30 Х% - 18	100% - У 60% - 18	100% - 30 60% - Z
Составим пропорцию	100 =30 Х 18	100=У 60 18	100=30 60 Z
Найдем неизвестный член пропорции	Х=100*18 30	У=100*18 60	Z= 60*30 100
Ответ	Девочки составляют 60 % от всех учащихся	В классе 30 учащихся	В классе 18 девочек

Эта таблица не дается учащимся сразу, а заполняется постепенно. После заполнения 1 колонки дается задание:

а) Составь обратные задачи по схемам 30,18, ;. , 18, 60%

30, , 60%.

б) Сформулируй обратные задачи

в) Запиши составленные задачи

г) Реши их.

Итак, рассмотрено 3 типа задач.

Попробуем им дать названия.

Вспомним схему, которой пользовались при решении задач на приведение к единице:

1 -

-

Закрывая последовательно «окошки», даем название типам задач: нахождение части от числа; нахождение числа по его части.

По аналогии: замени слово «часть» словом «процент».

2. Закрепление новых знаний.

1. Составь и реши по рисунку взаимно обратные задачи

Прямая Обратная

100% - 100% - Х

60% - У 60% -

\\\\\\\\\\\\\\\\\\\\\\\\\\\\\	\\\\\\\\\\\\\\\\\\\\\\\\\\\\\	\\\\\\\\\\\\\\\\\\\\\\\\\\\\\	\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\	\\\\\\\\\\\\\\\\\\\\\\\\\\\\\	\\\\\\\\\\\\\\\\\\\\\\\\\\\\\	\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\	\\\\\\\\\\\\\\\\\\\\\\\\\\\\\	\\\\\\\\\\\\\\\\\\\\\\\\\\\\\	\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\	\\\\\\\\\\\\\\\\\\\\\\\\\\\\\	\\\\\\\\\\\\\\\\\\\\\\\\\\\\\	\\\\\\\\\\\\\\\\\\\\\\\\\\\\

По схеме определи тип задачи, запиши схемы в соответствующие колонки таблицы, составь и реши задачи к данным схемам:

Нахождение процентов от числа	Нахождение числа по процентам	Нахождение процентного отношения
100% - 5.4 30% - Х	100% - Хр 7% - 21р	100% - 368т А% - 14,72т
100% - 500км 56% - Хкм	100% - Уц 30% - 1,62ц	100% - 165м У% - 10м

III. Переход к решению задач.

1.№ 372, стр.249.

а). Вес тела на Луне составляет 16% веса этого же тела на Земле. Сколько будет весить на Луне космонавт, если на Земле он весит 70кг.?

б). Составьте и решите обратную задачу на нахождение числа по его проценту:

100% - Хкг(Земля)

16% - 11,2 кг (Луна)

в). Вычисли свой вес на Луне.

2.№ 376(стр.251). В личной библиотеке было 400 единиц хранения. Из них 64 книги по математике, 240 — художественные, остальные - «Огонек».

Сколько процентов книг составляют книги по математике, художественные, «Огонек» отдельно. Изобрази рисунком.

б) По рисунку составь задачу на движение

IV. Сравнение способов решения задач на проценты

(задачи записать рядом)

Задача. С цены товара была сделана скидка 12р., что составило 15% первоначальной цены товара. Чему равна первоначальная цена? Сколько стоит товар после уценки? Реши с помощью пропорции и приведением к единице.

Способ I (пропорцией)	Способ II (приведение к единице)
1. 100% - Хр. 15% - 12р 100 = Х 15 12 Х= 100*12 15 Х= 80. 2. 80-12=68р. стоит товар после уценки	1. Чему =1%? 12: 15=0,8(р) 2. Чему = 100%? 0,8*100=80р. 3. Сколько стоит товар после уценки? 80-12=68 (р)

Ответ: 80р. - первоначальная цена 68р. - стоимость товара после уценки

Какой из способов вам интересен, рационален?

5. Решение более сложных задач на %.

Пусть банк выплачивает по сберегательному счету простые % по ставке А в год, причем эта ставка остается неизменной в течение двух лет. Вкладчик может поступить по-разному: 1) Если он закроет счет через год, то он получит сумму S(1) = S(0)x(1+A). Допустим, что он положит эту сумму ещё на 1 год с теми же условиями, тогда через второй год он получит S(2)=S(1)x (1+A)=S(0)x (1+A)²

S (2)= S(0)x (1+A) Равны ли эти суммы? Сравним их. S(0x1+A)²- S(0)x(1+2A)= S(0)x(1+2A+A-1-2A)=S(0)xA.

Так какой же способ выгоднее для вкладчика? Так как вкладчик получает при этом на S(0)xA больше, Величина S(0)xA — приращение на проценты, полученные за первый год или так называемые «проценты на проценты».

Чтобы предотвратить частое переоформление вкладов и для поощрения долгосрочных вкладов, в коммерческой практике принято выплачивать сложные проценты. Исходная сумма или база (S(0)) для начисления сложных процентов увеличивается с каждым периодом начисления, а для простых процентов база постоянна (S(0)).

Запишем определение.

Капитализацией процентов называется присоединение начисленных процентов к сумме, являющейся базой для их начисления. Выведем формулу расчета наращенной суммы.

S(n) с годовой процентной ставкой А при условии, что проценты начисляются и капитализируются один раз в год.

S(1)=S(0)+S(0)xA=S(0)x(1+A)

S(2)=S(1)+S(1)xA=S(1)x(1+A)=S(0)x(1+A)²

S(3)=S(0)x(1+A)³....................................

S(n)=S(0)x(1+A)ⁿ — формула сложных процентов, где S(n) - наращенная сума через n лет.

S(0) — базовая сумма.

Эта формула описывается геометрической прогрессией со знаменателем q=1+1.

Пример1.

Вы положили в банк 10 тысяч руб на срочный вклад при сложной процентной ставке 10% годовых. Сколько денег Вы получите через 2 года?

Дано: S(0)=10000руб., А=0,1, n=2, Найти S(2).

Решение

S(2)=S(0)x(1+A)². S(2)=10000x (1+0,1)²=10000x1,21=12100 руб.

Ответ: 12100руб.,

Отношение Q=S(n)= S(0)x(1+A)² = (1+A) ⁿ= Qc.

S(0) S(0)

Qc — коэффициент наращения по сложным процентам.

S(n)=S(0) x Qc

VI. Обобщение и систематизация знаний.

На таких уроках идет творческая работа по решению и составлению задач.

Выводы:

1. при такой методике исчезает необходимость изучения в 3 подтемах темы: «Проценты». Экономим время.

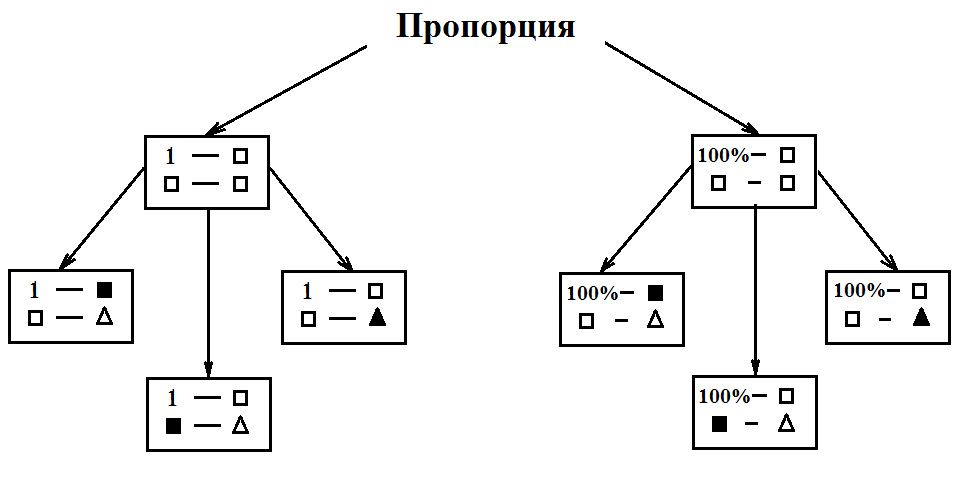
2. Повторение алгоритма решения задач, но не прямое, а преобразованное:

а) при решении задач на пропорции использовали схему -

-

б) при решении задач на дроби

1 -

-

в) при решении задач на проценты: 100% -

-

Тему понимают глубже.

3. Используя аналогию, сравнение, учатся выявлять сходство, различие, проявляют смекалку, сообразительность, учатся самостоятельности.

4. Открывается поле для творчества, появляется интерес; учащиеся - в фазе активной умственной деятельности.

5. Сравнение способов решения задач позволяет подходить к решению задач с разных позиций, учит не отступать, отстаивать свою точку зрения и побеждать в трудных случаях.

1.Влажность свежескошенной травы 70%, а влажность сена 16%. Сколько надо скосить травы, чтобы получить 1 т сена?

Решение. В 1 т сена сухой массы 840 кг (100-16%= 84%, 1000*0,84=840).В свежескошенной траве сухая масса составляет 30%. Значит, 840 кг составляют 30% и травы нужно скосить 840:0,3=2800(кг)=2.8(т).

2.Перерабатывая цветочный нектар в мед, пчелы освобождают его от значительной части воды. Нектар содержит 70% воды, а мед — 16%. Сколько килограммов нектара надо переработать для получения 1 кг меда?

(2,8 кг.)

3.Куб с ребром 8 см покрасили со всех сторон, а затем распилили на кубики с ребром 1 см. Какой процент среди них составляют кубики, имеющие только одну окрашенную грань?

Решение. 8*8*8=512 (кубиков) получится при распиле, и среди них с одной окрашенной гранью (6*6)*6=216 (кубиков);

512 кубиков — 100%,

216 кубиков — х%

х= 216*100 =42,1875.

512

(примерно 42,2%.)

4.В драматическом кружке число мальчиков составляет 80% от числа девочек. Сколько процентов составляет число девочек в этом кружке от числа мальчиков?

Решение. Пусть девочек х, тогда мальчиков0,8х. Число девочек составляет от числа мальчиков х *100%=125%

0,8х

5.Под кукурузу отвели участок поля в форме прямоугольника. Через некоторое время первоначальную длину участка увеличили на 35%, а ширину уменьшили на 14%. На сколько процентов изменилась площадь участка?

Решение. Пусть х — длина, у — ширина участка. Тогда его площадь ху. После изменения параметров длина его стала 1,35х, а ширина 0,86у. Площадь нового участка равна 1,35х*0,86у=1,161ху.

Значит, по сравнению с первоначальной площадью увеличилась на 1,161 ху-ху=0,161ху, что составляет 0,161ab *100% =16,1 %.

ab

6.В свежих грибах было 90% воды. Когда их высушили, то они стали легче на 15 кг при влажности 60%. Сколько было свежих грибов?

Решение. Если свежих грибов было х(кг), то сухой массы в них 0,1х (кг). После подсушивания сухой массы стало 40%, т.е. 0,1х (кг) составляет 40%, значит, при влажности 60% грибов стало 0,1х*100% =1х (кг), а испарилось 3х (кг)влаги, что составляет 15 кг., т. е. 40% 4 4

3х=15, х=20.

4

(20 кг свежих грибов.)

7.Имеется 735 г. 16%-ного раствора йода в спирте. Нужно получить 10%-ный раствор йода. Сколько граммов спирта надо долить для этого к уже имеющемуся раствору?

(441 г.)

8.Как изменится в процентах площадь прямоугольника, если его длина увеличится на 30%, а ширина уменьшится на 30%.

(Площадь уменьшится на 9%.)