муниципальное казённое общеобразовательное учреждение
«Красноярская средняя общеобразовательная школа»
Занятие кружка по подготовке учащихся 7-8 классов к олимпиаде по математике
тема: «Логические задачи»
Выполнила: Брайко Ольга Сергеевна
учитель математики
«Математику
уже затем учить надо,
что она ум в
порядок приводит»
М.В. Ломоносов
Введение
Работа учителя математики по–прежнему нацелена на прохождение программы, а не на развитие мышления у детей. При обучении математике на решение задач отводиться много учебного времени. Но чаще всего это текстовые задачи, при решении которых, главное внимание учащихся направлено на то, чтобы найти решение задачи и притом как можно быстрей. На нахождение способов решения, на анализ уже не остаётся времени, а ведь это едва ли - не главные аспекты решения задач. Получается, что учебного времени, отведенного на развитие логического мышления у учащихся на уроках в школе, недостаточно. Тем более чтобы научить ребят решению олимпиадных задач, среди которых обязательно присутствуют логические задачи. Главная задача в работе учителя – содействовать развитию познавательных возможностей у учащихся. На самом деле учащиеся испытывают затруднения при решении таких задач. Их решение требует от учащихся знаний, умений и навыков по различным разделам школьного курса математики и знание таких разделов как теория вероятности, статистика, комбинаторика. Самостоятельный поиск метода решения учеником таких задач минимален. Большинство учащихся, встретившись с задачей незнакомого или малознакомого вида, не знают, как к ней подступиться, с чего начать решение, и при этом обычно произносят печально известные слова: "А мы такие не решали". Поэтому появилась необходимость проведения таких занятий. Эффективное развитие математических способностей у учащихся невозможно без использования в учебном процессе задач на сообразительность, задач-шуток, ребусов, логических задач. На математических олимпиадах самые неожиданные трудности возникают именно при решении задач, в которых не предполагается никаких предварительных знаний из школьного курса, но требуется правильно уловить смысл вопроса и рассуждать последовательно. Одним из авторов алгебры высказываний (булевой алгебры) является английский математик Джорж Буль (1815-1864), который опубликовал следующие важные книги на эту тему «Математический анализ логики, сопровождаемый исчислением дедуктивных рассуждений», «Исследование законов мысли, на которых основаны математические теории логики и вероятности». Буль не считал логику разделом математики, но находил глубокую аналогию между символическим методом алгебры и символическим методом представления логических форм. В нашей стране первый курс лекций по математической логике был прочитан в 1887-1888году в Казанском университете Порецким Платоном Сергеевичем.
Сейчас же логика и задачи логические встречаются в каждом сборнике олимпиадных и конкурсных задач. Хотя эти задачи среди всех математических задач очень выделяются, т.к. в них, как правило, отсутствуют вычисления.
В наше время очень часто успех человека зависит от его способности четко мыслить, логически рассуждать и ясно излагать свои мысли. Именно поэтому развитие мышления является важной задачей школьного курса обучения. Умение правильно рассуждать необходимо в любой человеческой деятельности. Задача учителя – не просто давать знания, предусмотренные программой, а способствовать формированию высокого уровня логической культуры учащихся. При этом математика имеет огромные возможности для реализации этой цели.
Цель: Сформировать у школьников культуру мышления.
Задачи:
1. Познакомить с понятием «логическая задача».
2. Познакомить с алгоритмами
и методами их решения.
3. Подобрать
логические задачи, решаемые разными
методами.
Оборудование к занятию кружка:
-
Компьютер, проектор
-
Карточки с заданиями для работы на кружке
-
Карточки с домашним заданием
Ход мероприятия:
Вопрос для учащихся:
Как вы думаете, что такое логика? (презентация) (Ребята предлагают свои варианты ответа)
Ло́гика (др.-греч.)— «наука о правильном мышлении», «искусство рассуждения») - наука о законах мышления.
А что такое логические задачи?
Логическая задача — это некоторая проблемная ситуация описанная каким либо возможным образом (на естественном, математическом или логическом языке, в виде схемы, рисунка или любым другим способом) для разрешения которой необходимы только правильные (логические) рассуждения.
В основе логически правильного мышления лежат логические законы. Рассуждать логично — значит рассуждать в соответствии с законами логики.
Например: (решите устно задачу)
В корзине лежат 5 яблок. Вопрос: как разделить эти яблоки между пятью девочками, чтобы каждой девочке досталось по одному яблоку и чтобы одно яблоко осталось в корзине.
Ответ: надо дать четырем девочкам по яблоку, а пятой девочке - оставшееся яблоко вместе с корзиной.
На практике не всегда удаётся быстро найти способ решения и сами задачи не всегда бывают простыми. Чтобы научиться решать надо знать алгоритм решения задач.
Основные этапы решения логических задач
1 этап
– анализ условия задачи. Получив задачу,
первое, что нужно сделать, это разобраться
в том, что это за задача, каковы ее
условия, в чем состоят ее требования,
т.е. провести анализ задачи. Этот анализ
и составляет первый этап процесса
решения задачи. А
необходим он для того чтобы понять общую
ситуацию, описанную в задаче.
2 этап
– схематическая запись задачи. Анализ
задачи следует как-то оформить, записать,
для этого используются разного рода
схематические записи задач, построение
которых составляет второй этап процесса
решения.
А это для того чтобы выделить в задаче
данные и искомые, а в задаче на
доказательство - посылки и заключения.
3
этап
– поиск способа решения задачи. Анализ
задачи и построение ее схематической
записи необходимы главным образом для
того, чтобы найти способ решения данной
задачи. Поиск этого способа является
третьим этапом процесса решения.
Составление плана решения задачи,
пожалуй, является главным шагом на пути
ее решения. Правильно составленный план
решения задачи почти гарантирует
правильное ее решение. Но составление
плана может оказаться сложным и длительным
процессом.
4
этап
– осуществление решения задачи. Когда
способ решения задачи найден, его нужно
осуществить.
Решая задачу, проверяйте каждый свой
шаг, убеждайтесь, что он совершен
правильно. Иными словами, нужно доказывать
правильность каждого шага. Иногда при
реализации плана замените термины и
символы их определениями.
При решении
некоторых задач помогает совет:
"Воспользуйтесь свойствами данных
в условии объектов".
5 этап
– запись ответа. Этот этап включает в
себя три очень важных момента:
-
проверка решения задачи (после того как решение осуществлено необходимо убедиться, что это решение правильное, что оно удовлетворяет всем требованиям задачи);
-
исследование задачи (необходимо еще раз произвести исследование задачи, а именно установить, при каких условиях задача имеет решение и притом, сколько различных решений в каждом отдельном случае; при каких условиях задача вообще не имеет решения и т.д.)
-
формирование ответа задачи.
Сегодня
мы решим несколько задач разными
способами. Откройте карточки с заданиями
(см. приложение
1)
Методы решения
задач:
-
Метод рассуждений
Основная
идея метода: последовательно
проводя рассуждения по содержанию и
условию задачи сделать правильный
вывод. Этим способом обычно решают
несложные логические задачи.
В
методике рассуждений при решении задач
помогают:
чертежи, краткие записи,
умение выбирать информацию,
умение пользоваться правилом
перебора.
Задача № 1.
В адим,
Сергей и Михаил изучают различные иностранные
языки: китайский, японский и арабский.
На вопрос, какой язык изучает каждый из
них, один ответил: "Вадим изучает
китайский, Сергей не изучает китайский,
а Михаил не изучает арабский".
Впоследствии выяснилось, что в этом
ответе только одно утверждение верно,
а два других ложны. Какой язык изучает
каждый из молодых людей?
адим,
Сергей и Михаил изучают различные иностранные
языки: китайский, японский и арабский.
На вопрос, какой язык изучает каждый из
них, один ответил: "Вадим изучает
китайский, Сергей не изучает китайский,
а Михаил не изучает арабский".
Впоследствии выяснилось, что в этом
ответе только одно утверждение верно,
а два других ложны. Какой язык изучает
каждый из молодых людей?
Решение: Имеется три утверждения. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе - ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
Ответ: Сергей изучает китайский язык, Михаил - японский, Вадим - арабский.
Задача № 2. В поездке пятеро друзей - Антон, Борис, Вадим, Дима и Гриша, знакомились с попутчицей. Они предложили ей отгадать их фамилии, причём каждый из них высказал одно истинное и одно ложное утверждение:
Дима сказал: "Моя фамилия - Мишин, а фамилия Бориса - Хохлов". Антон сказал: "Мишин - это моя фамилия, а фамилия Вадима - Белкин". Борис сказал: "Фамилия Вадима - Тихонов, а моя фамилия - Мишин". Вадим сказал: "Моя фамилия - Белкин, а фамилия Гриши - Чехов". Гриша сказал: "Да, моя фамилия Чехов, а фамилия Антона - Тихонов".
Какую фамилию носит каждый из друзей?
Решение: Обозначим имена и фамилии заглавными буквами. Например: АБ, где буквы А и Б соответствуют начальным буквам имени и фамилии.
Зафиксируем высказывания каждого из друзей:
• ДМ и БХ;
• АМ и ВБ;
• ВТ и БМ;
• ВБ и ГЧ;
• ГЧ и АТ.
Допустим сначала, что истинно ДМ. Но, если истинно ДМ, то у Антона и у Бориса должны быть другие фамилии, значит АМ и БМ ложно. Но если АМ и БМ ложны, то должны быть истинны ВБ и ВТ, но ВБ и ВТ одновременно истинными быть не могут.
Значит, остается другой случай: истинно БХ. Этот случай приводит к цепочке умозаключений: БХ истинно БМ ложно ВТ истинно АТ ложно ГЧ истинно ВБ ложно АМ истинно.
Ответ: Борис - Хохлов, Вадим - Тихонов, Гриша - Чехов, Антон -Мишин, Дима - Белкин.
-
Метод таблиц
Основная
идея метода: При
использовании данного способа главное
– построить таблицу, строки которой
соответствуют элементам одного из
рассматриваемых в задаче множеств, а
столбцы – элементам другого.
Часто при решении логических
задач используют таблицы, в связи с тем,
что задачи могут содержать много условий,
которые все сразу трудно удержать в
голове. Поэтому ученики должны составить
таблицу. Она составляется при внимательном
прочтении и анализе условии задачи,
после чего вся содержащаяся информация
в задаче отображается в таблице. Такая
обработка условия данных задачи
значительно облегчает ее решение, а
иногда является единственным способом
решения. Таблицы не
только позволяют наглядно представить
условие задачи или ее ответ, но в
значительной степени помогают делать
правильные логические выводы в ходе
решения задачи.
Задача № 3: В каких квартирах живут котята?
В квартирах № 1, 2, 3 живут три котёнка - белый, чёрный, рыжий. В квартирах № 1 и 2 живут не чёрные котята. Белый котёнок живёт не в квартире № 1. В какой квартире, живёт какой котёнок?
|
Кто, Где? |
1 |
2 |
3 |
|
Б |
- |
+ |
- |
|
Ч |
- |
- |
+ |
|
Р |
+ |
- |
- |
Решение: 1. Так как чёрный котёнок не живёт в квартирах № 1 и 2 ( по условию ), значит, чёрный живёт в квартире № 3.
2. Так как чёрный живёт в квартире № 3 ( по доказательству ), значит белый и рыжий не живут в квартире № 3.
3. Так как белый котёнок не живёт в квартире № 1 ( по условию ) и не в квартире № 3 ( по доказательству ), значит, белый живёт - в № 2.
4. Так как белый живёт - в №2 ( по доказательству ), значит, рыжий не живёт - в №2.
5. Так как рыжий не живёт - в №2 и 3(по доказательству ), значит, рыжий живёт № 1.
Ответ: белый живёт в квартире № 2, чёрный - в № 3, рыжий - в № 1 .
Задача
№ 4: Кто есть кто? В одном
доме живут три товарища - школьники
Боря, Вася и Дима.
Один из них играет
в футбольной команде, другой пишет
стихи, а третий лучше своих друзей играет
в шахматы.
И звестно,
что: 1) Васин друг с огорчением сказал:
«Вчера я не сумел реализовать пенальти»;
2) товарищ поэта сказал: « Дима! Написал
бы ты стих и для нашей футбольной
команды». Назовите имена футболиста,
поэта и шахматиста.
звестно,
что: 1) Васин друг с огорчением сказал:
«Вчера я не сумел реализовать пенальти»;
2) товарищ поэта сказал: « Дима! Написал
бы ты стих и для нашей футбольной
команды». Назовите имена футболиста,
поэта и шахматиста.
Решение:
Из условия (1) видно, что Вася не является
футболистом,
а из условия (2), что Дима
- поэт и, значит, не футболист. Получили:
Боря -футболист, Дима - поэт, Вася -
шахматист.
Как видите, всё очень просто. Надо
только внимательно анализировать
условие и делать правильные выводы.
Ответ: Боря - футболист, Дима - поэт, Вася - шахматист.
-
Метод графов
Слово «граф» в математической литературе появилось совсем недавно. Понятие графа используется не только в математике, но и в технике и даже в повседневной жизни под разными названиями – схема, диаграмма.
Особенно большую помощь графы оказывают при решении логических задач. Представляя изучаемые объекты в наглядной форме, «графы» помогают держать в памяти многочисленные факты, содержащиеся в условии задачи, устанавливать связь между ними.
Основная идея метода: При использовании данного способа главное – построить граф — это совокупность объектов со связями между ними. Объекты представляются как вершины, или узлы графа (они обозначаются точками), а связи — как дуги, или рёбра. Употребляю сплошную или штриховую линии, или линии со стрелками.
Задача № 5: Между планетами введено космическое сообщение по следующим маршрутам: З-К, П-В, З-П, П-К, К-В, У-М, М-С, С-Ю, Ю-М, М-У. Можно ли добраться с З до М?
Решение: Составим схему-граф маршрутов: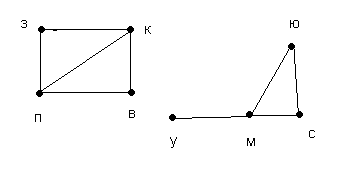
Мы видим, что от З до М добраться нельзя.
Ответ: нельзя.
Задача № 6: В кафе встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. «Замечательно, что у одного из нас белые, у другого черные ,а у третьего рыжие волосы, но ни у кого цвет волос не соответствует фамилии»,-заметил черноволосый. «Ты прав»,- сказал Белов. Какого цвета волосы у художника.
Решение: «Ни у кого цвет волос не соответствует фамилии» заметил черноволосый. «Ты прав»,- сказал Белов. Значит Белов не черноволосый. Белов может быть только рыжеволосым. Чернов белым, а Рыжов чёрным. Так как художником является Рыжов, а он черноволос, имеем ответ.
Ответ: художник черноволос
-
Метод кругов Эйлера.
Основная идея метода:
Задачи, в которых требуется
найти некоторое пересечение множеств
или их объединение, соблюдая условия
задачи.
Круги Эйлера —
геометрическая схема, с помощью которой
можно изобразить отношения между
подмножествами, для наглядного
представления.
Метод
Эйлера является незаменимым при решении
некоторых задач, а также упрощает
рассуждения. Однако прежде чем приступить
к решению задачи, нужно проанализировать
условие. Иногда с помощью арифметических
действий решить задачу легче.
Задача
№ 7: Ребята
из нашего класса любят мороженное.
Известно, что 15 ребят любят шоколадное,
11 – пломбир, из них 6 любят и шоколадное
и пломбир. Сколько человек любят пломбир?
Решение: Чертим
два множества следующим образом:
6
человек, которые любят и шоколадное и
пломбир, помещаем в пересечение
множеств.
15
– 6 = 9 – человек, которые любят только
шоколадное.
11
– 6 = 5 – человек, которые любят только
пломбир
Ответ: 5
человек любят только пломбир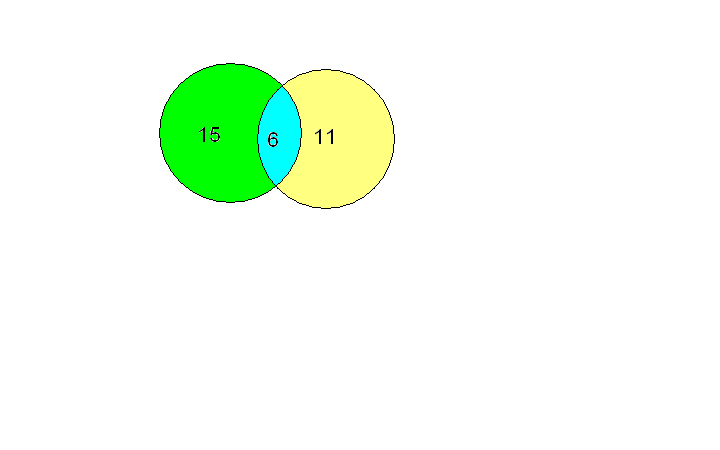
Задача № 8: Ребята нашего класса имеют возможность посещать три факультатива: по рисованию, по литературе и по математике. Известно, что 6 человек из класса посещает только математику, 2 – только рисование, 5 – только литературу. Только математику и рисование посещает 3 человека, рисование и литературу – 4, математику и литературу – 2. Один человек из класса посещает все три факультатива. Найти:
-
Сколько всего человек в классе?
-
Сколько человек посещает рисование?
-
Сколько человек посещает математику?
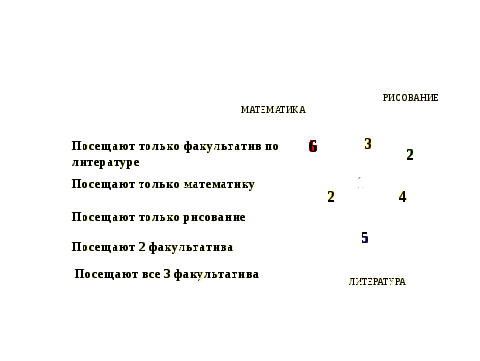
Решение: 1)Сначала отметим все области на кругах. На схеме видим, что для ответа на первый вопрос нужно сложить все числа:
6+2+5+3+4+2+1=23 (всего человек в классе)
2) Посещают рисование (складываем 4 числа, входящих в круг):
2+3+4+1=10
3) Посещают математику
6+3+1+2=12
Ответ: 23-всего, 10-рисование, 12-математика
Рефлексия (на доске незаконченные фразы)
-
сегодня я узнал…
-
было интересно…
-
было трудно…
-
я выполнял задания…
-
я понял, что…
-
теперь я могу…
-
я почувствовал, что…
-
я приобрел…
-
я научился…
-
у меня получилось …
-
я смог…
-
я попробую…
-
меня удивило…
-
урок дал мне для жизни…
-
мне захотелось…
Если
вы хотите научиться плавать, то смело
входите в воду, а если хотите научиться
решать задачи, то решайте их!
Д. Пойа
Вывод:
Истина и логика взаимосвязаны, поэтому значение логики невозможно переоценить. Логика помогает доказывать истинные суждения и опровергать ложные, она учит мыслить четко, лаконично, правильно. Логика нужна всем людям, работникам самых различных профессий.
Как
правило, задачу можно решить несколькими
способами. Чтобы выбрать наиболее
простой и эффективный способ для каждой
конкретной задачи, необходимо знать
все эти способы. Известно множество
различных способов решения логических
задач. Мы рассмотрели только некоторые
из них. Существуют ещё метод
математического бильярда, метод
блок-схем и пр.
Познакомившись
с разными видами логических задач и
методами их решения, вы сможете полученные
знания применить в своей учебной
деятельности, самостоятельно выбрать
тот или иной метод решения задачи,
применить изученные методы к решению
проблемы в реальной ситуации.
Цель
и задачи работы, которые были поставлены
в самом начале, решены.
Да,
существует много способов решения
различных логических заданий. Но, к
сожалению, решение их всех не может
быть сведено к какому-нибудь одному
методу, пригодному всегда. Поэтому у
вас всегда есть право выбора.
Д/з решить четыре задачи любым способом (см. приложение 1)
Список литературы
-
Севрюков П.Ф. Подготовка к решению олимпиадных задач по математике – М.: Илекса, 2007.
-
Бабинская И. Л. Задачи математических олимпиад /Москва: Наука 1975.
-
Мальцев Ю.Н., Саженков А.Н, Олимпиадные задачи по математике; Барнаул 1994.
-
Горбачев, Н.В. Сборник олимпиадных задач по математике— Москва: Просвещение, 2004.
-
МАТЕМАТИКА: Интелектуальные марафоны, турниры, бои; Москва, «Первое сентября», 2004
-
Мельников, О. И. Занимательные задачи по теории графов / О. И. Мельников. — Мн.: ТетраСистемс, 2001.
-
Шарыгин, И. Ф. Задачи на смекалку / И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2003.
Интернет-источники
Источник: 0zd.ru›matematika/metody_resheniya…zadach_i.html
Источник: http://5fan.ru/wievjob.php?id=96
Источник: http://5fan.ru/wievjob.php?id=96
- Контрольно-оценочная деятельность учителя начальных классов в условиях реализации ФГОС НОО
- Международный вебинар «Волонтёрство и новые воспитательные практики в школе»
- Международный вебинар «Обучение грамоте старших дошкольников с помощью развивающих игр В. В. Воскобовича: практика реализации ФГОС и ФОП ДО»
- Проектирование современного урока математики: реализация требований ФГОС
- Организация исследовательской и проектной деятельности обучающихся начальной школы как основное требование ФГОС НОО
- Методы и приемы формирования и оценки УУД младших школьников в соответствии с ФГОС НОО




