Инновации и современные технологии в обучении химии. Матричный прием.

Поиск курсов и вебинаров

Курсы переподготовки

Курсы повышения квалификации

Образовательные вебинары

Профессиональное обучение

IT Курсы

Обучение по охране труда

Все курсы и вебинары

Формат проведения

Любой

Занятия по расписанию (онлайн)

Круглосуточный доступ (офлайн)

Образоват. организация

Обучающая организация

Время проведения

Выберите даты проведения занятий: прошедшие или предстоящие.


янв	фев	мар	апр
май	июн	июл	авг
сен	окт	ноя	дек

По


янв	фев	мар	апр
май	июн	июл	авг
сен	окт	ноя	дек

Проходящие сейчас
Предстоящие по расписанию (онлайн)
Новые в круглосуточном доступе (офлайн)
Показать завершенные/регистрация завершена

Бесплатные

Действует акция

Льготный период сейчас

Сбросить

Файл прикреплен к материалу: Инновации и современные технологии в обучении химии. Матричный прием.

Сообщить о нарушении Войдите для скачивания файлов

Ряснова Людмила Григорьевна, учитель химии

МОУ «Лянторская СОШ №4»

Если вы хотите научиться плавать,

то смело входите в воду, а если хотите

научиться решать задачи, то решайте их!

Д. Пойа

Решение задач…«Интерес к решению, поиску решения, весьма вероятно, распространен шире, чем можно было бы предположить с первого взгляда. Место, которое занимают кроссворды и другие головоломки в популярных газетах и журналах, свидетельствует о том, что люди тратят известное время на решение задач, не имеющих практического интереса. За желанием решить ту или иную задачу, бесполезную в смысле материального выигрыша, может быть скрыто более глубокое любопытство, желание осознать пути и средства, приводящие к решению…» Д. Пойа.

«Воспитание творческой активности учащихся в процессе изучения ими математики является одной из актуальных целей нашего школьного преподавания. Правильно поставленное упражнение учащихся в решении задач — основное средство для достижения указанной цели. Вполне оправдано поэтому то повышенное внимание, которое уделяют этому аспекту преподавания математики передовые учителя нашей школы. Если обратиться, однако, к учебно-методической литературе по математике, будь то отечественной или иностранной, то приходится

констатировать, что при наличии большого количества в своем роде весьма ценных работ, посвященных методам решения отдельных типов математических задач (арифметических, конструктивно-геометрических и т. д.), до сего времени фактически отсутствовали труды, в

которых серьезно разрабатывалась бы общая методика решения математических задач. Между тем ознакомление лишь со специальными способами решения отдельных типов задач создает реальную опасность того, что учащиеся ограничатся усвоением одних шаблонных приемов и не приобретут умения самостоятельно справляться с «незнакомыми» задачами…»

Возможно, вы удивились, почему учитель химии статью, посвященную методике обучения решению химических задач, начал со слов о пробелах в методической литературе по математике…

Вы удивитесь ещё раз, когда узнаете, что первый абзац моей статьи заняла цитата из книги Д. П О Й А «КАК РЕШАТЬ ЗАДАЧУ» (Перевод с английского под редакцией Ю. М. ГАЙДУКА,

ПОСОБИЕ ДЛЯ УЧИТЕЛЕЙ, ГОСУДАРСТВЕННОЕ УЧЕБНО-ПЕДАГОГИЧЕСКОЕ ИЗДАТЕЛЬСТВО МИНИСТЕРСТВА ПРОСВЕЩЕНИЯ РСФСР, МОСКВА, 1959г.), если быть точнее, то это часть вступления к этой книге от редактора русского перевода.

Недостаточно лишь понять задачу,

необходимо желание решить её.

Без сильного желания решить трудную

задачу невозможно, но при наличии такового возможно.

Где есть желание, найдётся путь!

Д. Пойа

Мой не многолетний опыт обучению учащихся решению расчетных задач по химии, подвел меня к нескольким выводам. Я поняла необходимость разработки элективного курса «Решение расчетных задач по химии», в ближайшее время планирую заняться разработкой пропедевтического курса по химии для обучающихся 7 класса, в котором значимую часть отведу решению математической части химических расчетных задач.

До разработки программы и методического сопровождения элективного курса, на обычных уроках, для закрепления навыков решения расчетных задач по химии, я уже использовала тренажеры (в учебном пособии «Инновации и современные технологии в обучении химии», выпущенном Калининградским государственным университетом, Екатерина Кондратьевна Долгань именует такой методический прием матричным). При создании методического и дидактического сопровождения курса я сочла необходимым видоизменить и систематизировать «тренажеры», ведь важно, чтобы по завершению элективного курса мне удалось привести в действие и эффективным образом направить усилия ученика, затрудняющегося самостоятельно начать или продолжать решение задачи.

Примеры заданий матричного типа, используемых на занятиях элективного курса «Решение расчетных задач по химии»

Занятие №2. «Вычисление по химическим формулам»

Цель: продолжение формирования и закрепление навыка ВЫЧИСЛЕНИЙ: относительной молекулярной массы вещества; массы определенного количества, объема или числа структурных частиц вещества; числа структурных частиц вещества, содержащихся в определенном количестве, массе или объеме вещества; объема газа(при н.у.) определенного количества, массы или числа структурных частиц вещества. Обобщение основных понятий: относительная атомная и относительная молекулярная масса, количество вещества, масса, молярная масса, объем, молярный объем, число Авогадро, общее число структурных частиц вещества. Составление логической блок-схемы, объединяющей основные понятийные единицы занятия.

Решаем задачи второго занятия.

Матрица №1.

Укажите порядок действий в решении задач.

Произведите вычисления.

Запишите полученные данные в пустые ячейки матричного тренажера.

№ п/п	Вещ-во	Ar /Mr	M, г/моль	m, г	V, л (н.у.)	N	ν, моль
	He			20
	Ar				336
	O₂					6,023 · 10 ²²
	H₂						1,5
	CO₂					12,046 · 10 ²⁴
	CH₄				112
	Cl₂			7,1
	N₂					5,6
	SO₂					15,0575 · 10 ²³
	Ne						0,75

Решая задачи в матрице, учащийся выстраивает логическую цепь, объединяя в ней все основные понятия учебно-тренировочного занятия (тренинга). Матричные задания каждый раз стимулируют поиск решения на основе построенной логической схемы, как бы давая возможность неоднократно проверить свой способ мышления, придавая уверенность учащимся в рассуждениях и действиях при решении расчетных задач. Важно, что при подобных заданиях не возникает шаблонности мышления, напротив, на основе построенной логической цепи возникает алгоритм, исполнение которого приводит к повышению скорости мыслительных процессов.

№ п/п	Вещ-во	Ar /Mr	M, г/моль	m, г	V, л (н.у.)	N	ν, моль
1	He	4	4	20 (дано)			5
2	Ar				336 (дано)
3	O₂					6,023 · 10 ²²
4	H₂						1,5

Итогом удачного занятия можно считать совместное построение логической блок-схемы:

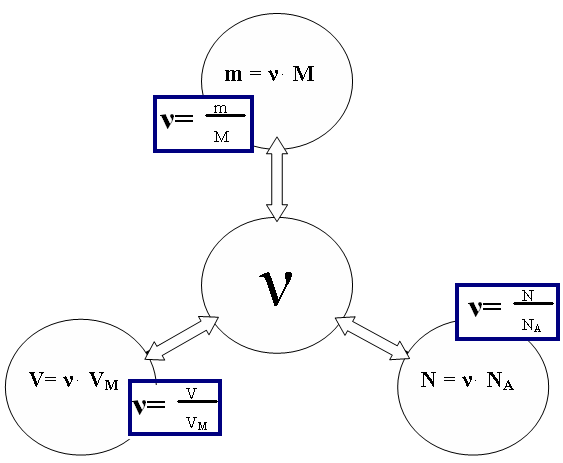
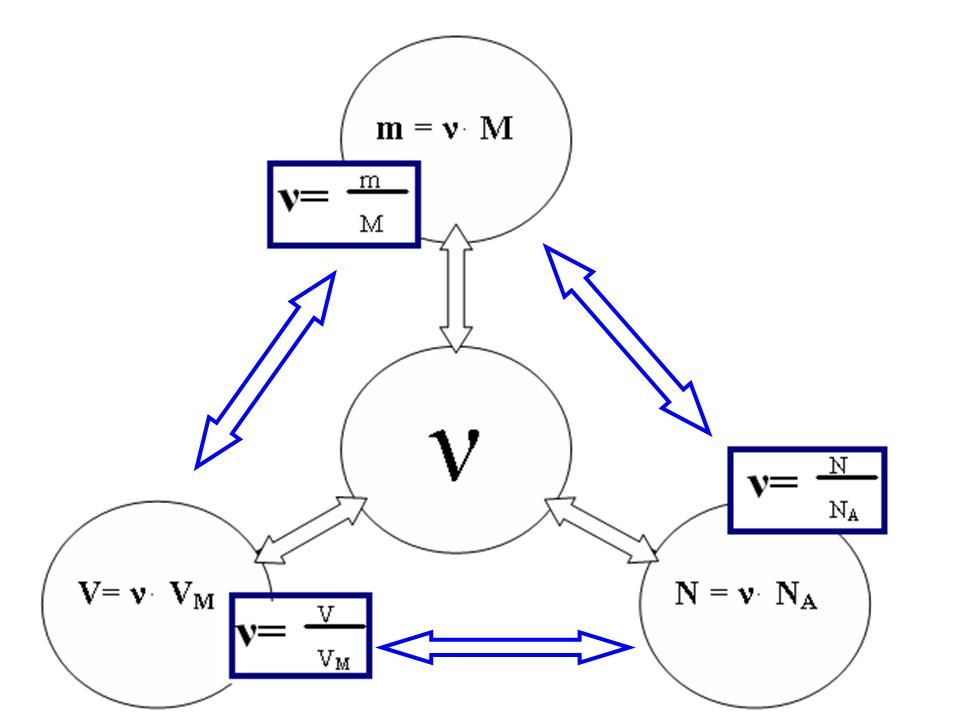
Занятие №4. «Задачи на растворы»

Цель: продолжение формирования и закрепление навыка ВЫЧИСЛЕНИЙ: массовой доли растворенного вещества (в %); массы растворенного вещества по известной массовой доле в растворе; массы растворителя. Составление логической блок-схемы, объединяющей понятия.

Решаем задачи четвертого занятия.

Матрица № 2.

Укажите порядок действий в решении задач.

Произведите вычисления.

Запишите полученные данные в пустые ячейки матричного тренажера.

№ п/п	ω вещества в растворе (в %)	m вещества, г	m растворителя, г	m раствора, г
	25			100
	5	30
		20	220
	15		300
			480	500
…	составь	задачу	соседу

Укажите порядок действий в решении задач.

Произведите вычисления.

Запишите полученные данные в пустые ячейки матричного тренажера.

№ п/п	ω вещества в растворе (в %)	m вещества, г	m растворителя, г	m раствора, г
1	25			100
2	5	30
3		20	220
4	15		300
…	составь	задачу	соседу

Можно усложнять задачи, добавляя другие величины, например, объем и плотность растворов, рассмотреть ситуации, связанные с концентрированием или разбавлением растворов, смешиванием двух или нескольких растворов…

Укажите порядок действий в решении задач.

Произведите вычисления.

Запишите полученные данные в пустые ячейки матричного тренажера.

№ п/п	ρ _р-ра, г/мл	V р-ра, мл	ω в-ва в растворе (в %)	m в-ва, г	m р-ля, г	m р-ра, г
1	1,8			90	150
2	1,1	500	3
3		300	5			330
4	1,2		10		50
5		120		15	135
…	составь	задачу	соседу

Усложним…

Укажите порядок действий в решении задач.

Произведите вычисления.

Запишите полученные данные в пустые ячейки матричного тренажера.

№ п/п	ω в-ва в растворе (в %)	m в-ва, г	m р-ля, г	m р-ра, г	+/- m р-ля, г	+/- m в-ва, г	ω' в-ва в растворе (в %)
1	10		100		+20	0
2		30		250	0	-15
3			200	220	0	+10
4	8	45	155			0	10
5	8	45	155		0		10
6			200	220	-20	+15
…	составь	задачу	соседу

Таким образом, усложняя задачи, можно выйти на решение комбинированных задач частей В и С ЕГЭ по химии, рассмотреть задачи олимпиад различных уровней.

Ваши лучшие пять друзей: Что, Почему, Где, Когда и Как. Если Вам нужен совет, обратитесь к Что, Почему, Где, Когда и Как — и больше ни к кому не обращайтесь. Ничему не верьте, но сомневайтесь только в том, что вызывает сомнение. Найдя первый гриб или сделав первое открытие, осмотритесь вокруг, - они родятся пучками. Д. Пойа

Считаю целесообразным познакомить учащихся со стратегией решения задач Д. Пойа:

Как решать задачу?

ПОНИМАНИЕ ПОСТАНОВКИ ЗАДАЧИ

Нужно

ясно

понять задачу.

Что неизвестно? Что дано? В чем состоит условие? Возможно ли удовлетворить условию? Достаточно ли условие для определения неизвестного? Или недостаточно? Или чрезмерно? Или противоречиво? Введите подходящие обозначения. Разделите условие на части. Постарайтесь записать их.

СОСТАВЛЕНИЕ ПЛАНА РЕШЕНИЯ

Нужно найти

связь между

данными и

неизвестным.

Если не удается сразу

обнаружить

эту связь,

возможно,

полезно будет рассмотреть вспомогательные

задачи. В конечном счете

необходимо

прийти к плану решения.

Не встречалась ли вам раньше эта задача? Хотя бы в несколько другой форме? Известна ли вам какая-нибудь родственная задача? Не знаете ли закона, теории, формулы, которые могли бы оказаться полезными? Рассмотрите неизвестное! И постарайтесь вспомнить знакомую задачу с тем же или подобным неизвестным.

Вот задача, родственная с данной и уже решенная. Нельзя ли воспользоваться ею? Нельзя ли применить ее результат? Нельзя ли использовать метод ее решения? Не следует ли ввести какой-нибудь вспомогательный элемент, чтобы стало возможно воспользоваться прежней задачей? Нельзя ли иначе сформулировать задачу? Еще иначе? Вернитесь к определениям. Если не удается решить данную задачу, попытайтесь сначала решить сходную. Нельзя ли придумать более доступную сходную задачу? Более общую? Более частную? Аналогичную задачу? Нельзя ли решить часть задачи? Сохраните только часть условия, отбросив остальную часть: насколько определенным окажется тогда неизвестное; как оно сможет меняться? Нельзя ли извлечь что-либо полезное из данных? Нельзя ли придумать другие данные, из которых можно было бы определить неизвестное? Нельзя ли изменить неизвестное, или данные, или, если необходимо, и то и другое так, чтобы новое неизвестное и новые данные оказались ближе друг к другу? Все ли данные вами использованы? Все ли условие? Приняты ли вами во внимание все существенные понятия, содержащиеся в задаче?

ОСУЩЕСТВЛЕНИЕ ПЛАНА

Нужно осуществить

план решения.

Осуществляя план решения, контролируйте каждый свой шаг. Ясно ли вам,

что предпринятый вами шаг правилен? Сумеете ли доказать, что он правилен?

ВЗГЛЯД НАЗАД

(изучение полученного решения)

Нужно изучить найденное решение.

Нельзя ли проверить результат? Нельзя ли проверить ход решения? Нельзя ли получить тот же результат иначе? Нельзя ли усмотреть его с одного взгляда?

Нельзя ли в какой-нибудь другой задаче использовать полученный результат

или метод решения?

КАК ИСКАТЬ РЕШЕНИЕ?

(Сокращенный вариант таблицы)

1. Понять предложенную задачу.

2. Найти путь от неизвестного к данным, если нужно, рассмотрев промежуточные задачи («анализ»).

3. Реализовать найденную идею решения {«синтез»).

4. Решение проверить и оценить критически.

1. Что гласит задача? Что дано? Что нужно найти? Определено ли неизвестное данными задачи? Или они недостаточны, или же чрезмерны? Нельзя ли сформулировать задачу иначе? Нельзя ли найти связь между данной задачей и какой-нибудь задачей с известным решением? Или с задачей, решающейся проще? Решающейся сразу? Эти вопросы нужно повторять каждый раз, когда в ходе

решения наступает заминка, при решении каждой промежуточной задачи. Кроме того: Все ли данные задачи были уже использованы?

2.Сформулировать отношение (или отношения) между неизвестным и данными. Преобразовать неизвестные элементы. Попытаться ввести новые неизвестные, более близкие к данным задачи. Преобразовать данные элементы. Попытаться получить, таким образом, новые элементы, более близкие к искомым неизвестным. Решить только часть задачи. Удовлетворить только части условий: насколько неопределенным окажется тогда неизвестное? Обобщить. Рассмотреть частные случаи. Применить аналогию.

3. Испытывать правильность каждого шага, принимая лишь то, «что усматривается с полной ясностью или выводится с полной достоверностью" (Декарт)

4. Правдоподобен ли результат? Почему? Нельзя ли сделать проверку? Нет ли другого пути, ведущего к полученному результату? Более прямого пути? Какие результаты еще можно получить

на том же пути?

Примером макростратегии может быть стратегия решения химической задачи одного из старшеклассников.

Стратегия решения химической задачи:

Прочитал текст задачи несколько раз, пытаясь представить реальную ситуацию.
Определил, какие вещества исходные, а какие — получаемые.
Представил запись возможного уравнения реакции, выделяя зрительно знак «=», левую и правую стороны уравнения.
Сразу вспомнилось уравнение реакции, написанное в учебнике.
Проанализировал, какие данные имеются в задаче.
Спросил себя, достаточно ли данных?
На черновике написал уравнение реакции, сверив вещества с имеющимися в тексте.
Уравнял коэффициенты.
Подписал сверху над уравнением реакции данные задачи.
Проверил, все ли данные находятся в одинаковых единицах измерения.
Мысленно увидел возможную пропорцию.
Записал пропорцию.
Представил «крестик» со знаком вопроса в левом углу пропорции.
Сделал вычисления по пропорции на калькуляторе.
Сравнил ответ с указанным в задачнике.
Оформил краткую запись условия и решения задачи, как учили: дано, данные задачи, уравнение реакции, ход решения.
Записал ответ.
Проверил, что ответ соответствует единицам измерения, которые требуются в задаче.

Дистанционное обучение педагогов по ФГОС по низким ценам

Вебинары, курсы повышения квалификации, профессиональная переподготовка и профессиональное обучение. Низкие цены. Более 18300 образовательных программ. Диплом госудаственного образца для курсов, переподготовки и профобучения. Сертификат за участие в вебинарах. Бесплатные вебинары. Лицензия.

Подробнее

Все образовательные вебинары

Подписаться на новые Расписание вебинаров

Стратегия решения химической задачи:

Дистанционное обучение педагогов по ФГОС по низким ценам

Поможем подобрать программу для Вас!