Стратий Екатерина Генадиевна, учитель математики 1 квалификационная категория.

Краснодарский край Славянский район ст. Анастасиевская ул. Продольная 142 г.

МБОУ СОШ № 25

Дисциплина: математика.

Учебник: Алгебра. 7 класс: учеб. для общеобразоват. учреждений /[Ю.Н. Макарычев, Н.Г.Миндюк, К.И. Нешков, С.Б. Суворова]; под ред. С.А.Теляковского.

Урок.

Класс: 7.

Продолжительность урока 40 минут.

Решение линейных уравнений зависящих от параметра.

Тип занятия – ознакомление с новым материалам.

Цель 1. Образовательная – научить учащихся находить значение параметров, при которых уравнение имеет рациональные корни, повторить теоретический материал по теме линейные уравнения.

2. Развивающая – развивать логическое мышление, анализ получения ответа, абстрактное мышление, математическую речь, вырабатывать самооценку в выборе пути.

3. Воспитательная - прививать интерес к предмету, воспитать стремление к достижению цели.

Ход урока

I. Организационный момент.

Приветствия класса.

II. Повторение пройденного материала, необходимого для перехода к новому.

Учитель. 1)Какое уравнение называется линейным? (Ответ: Уравнение вида ах + в=0, где х – переменная, а, в – некоторые числа.)

2) Сколько решений имеет уравнение ах + в=0, если

(условия а) – г) заранее записаны на доске)

а) а ≠ 0, в ≠ 0; (Ответ: х= - )

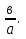б) а ≠ 0, в=0; (Ответ: х=0.)

в) а = 0, в ≠ 0; (Ответ: решений нет.)

г) а = 0, в = 0. (Ответ: бесконечное множество решений.)

Вывод: 1) уравнение имеет единственное решение;

2) не имеет решение;

3) имеет бесконечное множество решений.

III. Объяснение нового материала.

Учитель. Ребята, сегодня мы с вами рассмотрим решение уравнений с параметрами. Для вас эта тема совершенно новая, на данная тема базируется на знаниях по теме «Линейные уравнения».

Учащиеся записывают тему в тетрадь, четко ставиться цель урока.

Учитель. Обратимся к виду линейного уравнения ( уравнение ах + в=0, записано на доске) , в нем коэффициенты а и в играют роль параметров. Например, уравнение (а – 1)х + 4=0, линейное уравнение с параметром а, х - независимая переменная, уравнение вида 2вх + 2в + +1 = 0, также линейное уравнение с параметром, где в – параметр, х - независимая переменная.

Учитель. Ребята, приведите примеры линейных уравнений с параметрами, 1- 2 примера. (Учитель ходит между рядами и проверяет.)

Учитель. При решении уравнений с параметрами будем использовать значения параметра, при переходе через которые происходят качественные изменения уравнения, эти значения параметра назовем особыми.

Учащиеся записывают определение.

Определение. Особыми - называются значения параметров, при переходе через которые происходят качественные изменения уравнения.

Учитель вместе с учащимися решает пример №1, №2, №3.

Пример № 1. Решить уравнение (а – 1)х + 4=0.

Решение

Особыми здесь являются те значения параметра а , при которых коэффициенты при х обращаются в нуль. Рассмотрим решение при а = 1, и

а ≠ 1.

а = 1 – особое значение параметра.

Если а = 1уравнение примет вид: 0 х = - 4, решений нет.

Если а ≠ 1, то х = - .

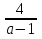Ответ: Если а = 1, решений нет, если а ≠ 1, то х = - .

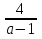Пример № 2. Решить уравнение 2(а + 2)х=(а + 2).

Решение

а= - 2 – особое значение.

Если а = - 2, то 0 х=0 – бесконечное множество решений, если а ≠ -2, то 2(а +2)х=(а + 2)

х = ,

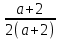х = .

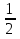Ответ: Если а = - 2, - бесконечное множество решений, если а ≠ -2, то

х = .

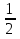Учитель. Ребята, какие у вас возникли вопросы в ходе решения. (Учитель отвечает на возникшие вопросы.)

Пример № 3. Решить уравнение а(2 – а)х + 4а + 1 = 0.

Решение

Учитель. 1) Назовите особые значения параметра. (Ответ: а = 2, а = 0 – особые значения.)

2) Почему данные значения являются особыми? (Ответ: коэффициент при х обращается в ноль.)

Если а = 0, решений нет, если а = 2, решений нет, если а ≠ о, а ≠ 2, то

х = .

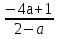Ответ: Если а = 0, а = 2, решений нет, если а ≠ о, а ≠ 2, то х = .

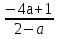Один ученик вызывается к доске решать пример № 4, остальные решают в тетрадях.

Пример № 4. Решить уравнение а(3 – а)х + 4а = 1

Решение

х = 0, х = 3 – особые значения.

Если а = о, то 0 х=1, решений нет; если а = 3, 0 х= - 11, решений нет, если а ≠ 0, а ≠ 3, то

х = .

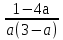Ответ: Если а = о, а = 3, если а ≠ 0, а ≠ 3, то х = .

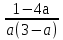Учащимся предлагается решить самостоятельно решить пример № 5. Учитель ходит между рядами проверяет, индивидуально работает с учащимися, у которых данная тема вызывает трудности.

Пример № 5. Решить уравнение 2а(а + 4)х = 2а + 1.

Решение

а = 0, а = - 4 – сосбые решения.

Если а = 0, 0 х=1, решений нет; если а = - 4, 0 х= - 7, решений нет; если а ≠ 0, а ≠ - 4, то х = .

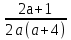Ответ: Если а = 0, а = - 4, решений нет; если а ≠ 0, а ≠ - 4, то х = .

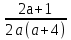Учитель. Вспомним формулы сокращенного умножения.

Например, а² – 9=(а – 3)(а + 3).

Учитель вместе с учащимися решает пример № 6.

Пример № 6. Решить уравнение (а² – 9)х=а² + 2а + 1.

Решение

Разложим выражение при х на множители, получим:

(а – 3)(а + 3)х = а² + 2а + 1.

а = 3, а = - 3 – особые значения.

Если а = 3, то 0 х = 16, решений нет; если а = - 3, то 0 х = 4, решений нет; если а ≠ ±3, то х= =.

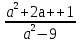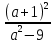Ответ: Если а = 3, а = - 3, решений нет; если а ≠ ± 3, то х=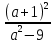 . Один ученик выходит к доске и решает пример № 7, оставшиеся решают в тетрадях.

Пример № 7. Решить уравнение (а² – 4)х= 2а + 3.

Решение

а = 2, а= = - 2 – особые значения.

Если а = 2, то 0 х = 7, решений нет; если а = - 2, то 0 х = - 1, решений нет; если а ≠ ± 2, то х= .

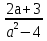Ответ: Если а = ±2, решений нет; если а ≠ ± 2, то х=.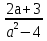

IV. Постановка домашнего задания.

1. Просмотреть материал занятия.

2. Решить пример № 8, №9.

Пример № 8. Решить уравнение а(а + 8)х = - 4а + 1.

Пример №1. Решить уравнение (9 – а²)х = 3а – 2.

V. Подведения итогов.

Учитель. Какая тема сегодняшнего занятия?

Назовите обстоятельства которые учитываются при решении линейных уравнений с параметрами? ( Ответ: обращение в нуль коэффициента при х).

литература

1. Учебник Алгебра. 7 класс: учеб. для общеобразоват. учреждений /[Ю.Н. Макарычев, Н.Г.Миндюк, К.И. Нешков, С.Б. Суворова]; под ред. С.А.Теляковского – М: Просвещение, 2011.

2. Ястребенецкий Г.А. Задачи с параметрами: Кн. для учител. – Просвещение, 1986.

3. Голубев В.И., Гольдман А.М.Дорофеев Г.В О параметрах с самого начала// Журнал Репетитор, 1991. № 2 – стр 3-13.