Методическое пособие для учителей математики и учащихся 9-11 классов по теме: « Случайные события и их вероятности»

Составил:

учитель МОБУ «СОШ с. Веденка»

Поздышева Н.С.

2017 г.

С 2012 года в ОГЭ и ЕГЭ вошли задания по теории вероятности. Изначально это были простейшие задачи на классическое определение вероятности, в которых рассматривались опыты с равновозможными элементарными исходами. Но в дальнейшем стали появляться задачи с более сложными схемами решения. Поскольку спектр задач расширился, то возникла потребность в данных методических рекомендациях.

Введение

Опр. Элементарные события (элементарные исходы) опыта – это простейшие события, которыми может окончиться опыт.

В результате эксперимента всегда происходит один и только один из его исходов. То есть, с одной стороны, не могут произойти сразу два исхода, а с другой – эксперимент не может завершиться вообще без какого-либо исхода.

Опр. События называются несовместными, если появление одного из них исключает появление других (не могут происходить одновременно).

Классическим примером несовместных событий является результат подбрасывания монеты – выпадение лицевой стороны исключает выпадение обратной стороны (в одном и том же опыте).

Опр. Полной группой событий называется совокупность всех возможных результатов опыта.

Опр. Событие, которое в данном опыте обязательно наступит, называют достоверным событием. Достоверному событию соответствует множество всех исходов опыта Ω.

Опр. Событие, которое в данном опыте наступить не может, называют невозможным событием. Невозможному событию соответствует пустое множество исходов .

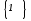Опр. Вероятностью случайного события А называется число Р(А), к которому приближается относительная частота этого события в длинной серии экспериментов.

Вероятность события А равна сумме вероятностей элементарных событий, благоприятствующих этому событию. Сумма вероятностей всех элементарных исходов опыта равна 1.

Опр. События называются равновероятными (равновозможными), если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.

Опр. Событие 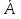, состоящее из тех и только тех элементарных исходов опыта, которые не входят в А, называется противоположным событию А. Вероятности противоположных событий связаны равенством:

.

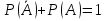Опр. Объединением событий А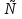В – событие, состоящее из элементарных исходов, благоприятствующих хотя бы одному из событий А, В.

Опр. Пересечение событий А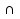В – событие, состоящее из элементарных исходов, благоприятствующих обоим событиям А и В.

Классическая вероятностная схема

Для нахождения вероятности события А при проведении некоторого опыта следует:

1. Определить, что является элементарным событием (исходом) в данном случайном эксперименте (опыте).

2. Найти общее число элементарных событий N.

3. Определить, какие элементарные события благоприятствуют интересующему нас событию А, и найти их число N(A). (Событие можно обозначить любой буквой.)

4. Найти вероятность события А по формуле .

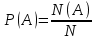Пример 1. Вася, Петя, Коля и Леша бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должен будет Леша.

Решение. Элементарное событие в этом эксперименте – участник, который выиграл жребий. Перечисляем их:

(Вася), (Петя), (Коля), (Леша)

Общее число элементарных исходов N равно 4.

Событию А={жребий пал на Лешу} благоприятствует только одно элементарное событие (Леша). Поэтому N(A)=1. Тогда

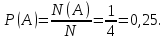
Ответ: 0,25.

Пример 2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно 1 раз.

Решение. Орел обозначим буквой О. Решку – буквой Р. В описанном эксперименте могут быть следующие равновозможные элементарные исходы:

ОО, ОР, РО и РР.

Значит, N=4.

Событию А = {выпала ровно одна решка} благоприятствуют элементарные события ОР и РО. Поэтому N(A)=2. Тогда

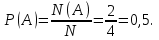
Ответ: 0,5.

Пример 3. В случайном эксперименте бросают две игральные кости. Найти вероятность того, что в сумме выпадет 6 очков.

Решение. Элементарный исход в этом опыте – пара чисел. Первое число выпадает на первой кости, а второе – на второй. Множество элементарных исходов удобно представить таблицей. Строки соответствуют результату первого броска, столбцы – результату второго броска. Всего элементарных событий N=6²=36.

	1	2	3	4	5	6
1					*
2				*
3			*
4		*
5	*
6

Поставим * в ячейках, где сумма равна 6. Таких ячеек 5. Значит, событию А = {сумма очков равна 6} благоприятствует 5 элементарных исходов, т.е N(A)=5. Поэтому,

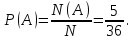
Ответ: .

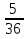В следующих задачах явно выписывать все элементарные исходы сложно, но достаточно легко подсчитать их количество.

Пример 4. В среднем из 1000 аккумуляторов, поступивших в продажу, 7 неисправны. Найти вероятность того, что один купленный аккумулятор окажется исправным.

Решение. Элементарный исход – случайно выбранный аккумулятор. Поэтому N=1000.

Событию А = {аккумулятор исправлен} благоприятствует 1000 - 7=993 исхода. Поэтому N(A)=993. Тогда

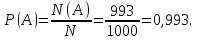
Ответ: 0,993.

Пример 5. В группе иностранных туристов 51 человек, среди них два француза. Для посещения маленького музея группу случайным образом делят на три подгруппы, одинаковые по численности. Найдите вероятность того, что французы окажутся в одной подгруппе.

Решение. В каждой подгруппе 17 человек. Присвоим французам номера – первый и второй. Будем считать, что первый француз уже занял место в какой-то подгруппе (назовем ее подгруппа А). Нужно найти вероятность того, что второй француз оказался в той же подгруппе А.

Для второго француза остается N=50 мест, из них в подгруппе А N(A)=16 мест. Размещение туристов, по условию, случайно, значит, комбинации равновозможны. Поэтому вероятность того, что второй турист попадет в подгруппу А, равна

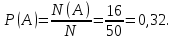
Ответ: 0,32.

Пример 6. Какова вероятность того, что случайно выбранное натуральное число от 82 до 96 делится на 6?

Решение. Общее число элементарных исходов N=15 (количество чисел от 82 до 96). Событию А={выбранное число делится на 6} благоприятствует N(A)=3 исхода (84, 90, 96). Тогда

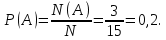
Ответ: 0,2.

Пример 7. На семинар приехали 4 ученых из Норвегии, 2 из Испании и 6 из Италии. Порядок докладов определяется жеребьевкой. Найти вероятность того, что одиннадцатым окажется доклад ученного из Италии.

Решение. Задачи данного типа можно решить по формуле Баесса, но достаточно принять равновозможным порядок докладов и тогда вероятность не будет зависеть от того кто в какой день делает доклад.

Общее число исходов N=12. Число исходов N(A), благоприятствующих событию А={доклад ученного из Италии} равно 6.

Тогда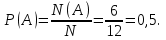

Ответ: 0,5.

Пример 8. Вероятность того что новая шариковая ручка пишет плохо (или не пишет), равна 0,05. Покупатель в магазине выбирает одну новую ручку. Найти вероятность того, что эта ручка пишет хорошо.

Решение. Определим событие:

А={выбранная ручка пишет хорошо}.

Известна вероятность противоположного события:

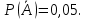
Используя формулу вероятности противоположного события:

P(A)=1-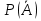=1-0,05=0,95.

Ответ: 0,95.

Пример 9. Перед началом волейбольного матча судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда «Байкал» по очереди играет с командами «Амур», «Енисей», «Вилюй» и «Иртыш». Найти вероятность того, что ровно в двух матчах право владеть мячом выиграет команда «Байкал».

Решение. Пусть 1 – команда «Байкал» владеет мячом первая, 0 – не владеет мячом. Первая комбинация во всех играх 1111, т.е во всех играх «Байкал» первый. Вторая комбинация 1110, т.е «Байкал» в первых трех играх первый.

Итого:

Всего исходов – 16, из них благоприятных – 6.

Вероятность данного события

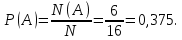
Ответ: 0,375.

Теоремы сложения и умножения вероятностей

Теорема сложения вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

P(A+B)=P(A)+P(B).

Пример 10. На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,1. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к двум темам, нет. Найти вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение. События А= {вопрос на тему «Тригонометрия»} и В={ вопрос на тему «Внешние углы»} несовместны. Тогда P(A+B)=P(A)+P(B)=0,1+0,15=0,25.

Ответ: 0,25.

Пример 11. Найти вероятность того, что при броске игрального кубика выпадет 2 или 5.

Решение: События А= {выпадет 2} и В={ выпадет 5} несовместны. Поскольку Р(А)=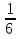 и Р(В)=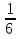, тогда P(A+B)=P(A)+P(B)=.

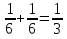Ответ: .

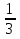Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

P(A+B)=P(A)+P(B) – Р(АВ).

Пример 12. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решeние. Рассмотрим события

А = кофе закончится в первом автомате,

В = кофе закончится во втором автомате.

Тогда

A·B = кофе закончится в обоих автоматах,

A + B = кофе закончится хотя бы в одном автомате.

По условию P(A) = P(B) = 0,3; P(A·B) = 0,12 .

События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:

P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48.

Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52.

Ответ: 0,52.

Опр. События А и В называются независимыми, если появления одного из них не влияет на вероятность появления другого.

Теорема умножения для независимых событий. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

.

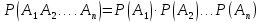Пример 13. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найти вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлить до сотых.

Решение. В этой задаче предполагается, что результат каждого следующего выстрела не зависит от предыдущих. Поэтому события {попал при первом выстреле}, {попал при втором выстреле} и т.д. независимы. Вероятность каждого попадания равна 0,8. Значит, вероятность каждого промаха равна 1 – 0,8=0,2. Воспользуемся формулой умножения вероятностей независимых событий. Получаем, что событие А={попал; попал; попал; промахнулся; промахнулся} имеет вероятность

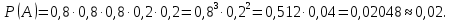
Ответ: 0,02.

Формула полной вероятности

Теорема. Вероятность событии А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) 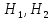, образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:

, (*)

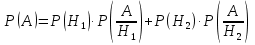где .

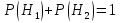Равенство (*) называют формулой полной вероятности.

Пример 14. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая – 55%. Первая фабрика выпускает 5% бракованных стекол, а вторая – 3%. Найти вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Решение. Событие А={купленное стекло окажется бракованным}. Гипотезы Н₁={стекло с первой фабрики}, Н₂={стекло со второй фабрики} образуют полную группу поскольку для Р(Н₁)=0,45 и Р(Н₂)=0,55 суммарная вероятность равна 1.

Условные вероятности 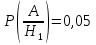, 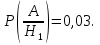Тогда

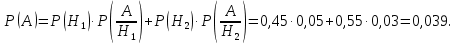
Ответ: 0,039.

Пример 15. В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок производит один выстрел из наудачу взятой винтовки.

Решение. Событие А={мишень будет поражена}. Гипотезы Н₁={винтовка с оптическим прицелом}, Н₂={ винтовка без оптического прицела} образуют полную группу поскольку для Р(Н₁)=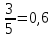 и Р(Н₂)= 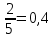суммарная вероятность равна 1.

Условные вероятности 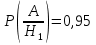, 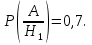Тогда

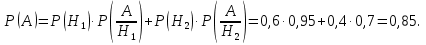
Ответ: 0,85.

Формула Бернулли

Пусть рассматриваются независимые испытания, в каждом из которых вероятность появления события одинакова.

Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0<p<1), событие наступит ровно k раз (безразлично в какой последовательности), равна

,

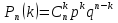где 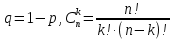–число сочетаний.

Пример 16. Биатлонист попадает в мишень с вероятностью 0,9. Он стреляет пять раз. Найти вероятность того, что он:

А) попадет все пять раз;

В) попадет ровно один раз;

С) не попадет в мишень ни одного раза.

Решение.

А) Согласно формуле Бернулли при k=5 и q=0,1 имеем:

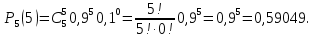
В) При k=1 имеем

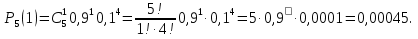
С) При k=0 имеем

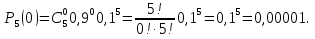
Ответ: 0,59049; 0,00045; 0,00001.

Список литературы

1. А.Г. Мордкович. События. Вероятности. Статистическая обработка данных: доп. Параграфы к курсу алгебры 7-9 кл. общеобразоват. Учреждений / А.Г. Мордкович, П.В. Семенов. – 6-е изд. М.: Мнемозина, 2009. – 112 с.: ил.

2. Математика. Методический журнал для учителей математики. Издательский дом «Первое сентября», январь 2012.

3. Е.А. Бунимирович, В.А. Булычев. Вероятность и статистика в курсе математики общеобразовательной школы. 1-4 лекции. М.: Педагогический университет «Первое сентября», 2011. – 128 с.

4. Е.А. Бунимирович, В.А. Булычев. Вероятность и статистика 5-9 кл.: Пособие для общеобразоват. учеб. Заведений. – М.: Дрофа, 2002. – 160 с.: ил.

Методическое пособие для учителей математики и учащихся 9-11 классов по теме: « Случайные события и их вероятности»

Составил:

учитель МОБУ «СОШ с. Веденка»

Поздышева Н.С.

2017 г.

С 2012 года в ОГЭ и ЕГЭ вошли задания по теории вероятности. Изначально это были простейшие задачи на классическое определение вероятности, в которых рассматривались опыты с равновозможными элементарными исходами. Но в дальнейшем стали появляться задачи с более сложными схемами решения. Поскольку спектр задач расширился, то возникла потребность в данных методических рекомендациях.

Введение

Опр. Элементарные события (элементарные исходы) опыта – это простейшие события, которыми может окончиться опыт.

В результате эксперимента всегда происходит один и только один из его исходов. То есть, с одной стороны, не могут произойти сразу два исхода, а с другой – эксперимент не может завершиться вообще без какого-либо исхода.

Опр. События называются несовместными, если появление одного из них исключает появление других (не могут происходить одновременно).

Классическим примером несовместных событий является результат подбрасывания монеты – выпадение лицевой стороны исключает выпадение обратной стороны (в одном и том же опыте).

Опр. Полной группой событий называется совокупность всех возможных результатов опыта.

Опр. Событие, которое в данном опыте обязательно наступит, называют достоверным событием. Достоверному событию соответствует множество всех исходов опыта Ω.

Опр. Событие, которое в данном опыте наступить не может, называют невозможным событием. Невозможному событию соответствует пустое множество исходов .

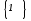Опр. Вероятностью случайного события А называется число Р(А), к которому приближается относительная частота этого события в длинной серии экспериментов.

Вероятность события А равна сумме вероятностей элементарных событий, благоприятствующих этому событию. Сумма вероятностей всех элементарных исходов опыта равна 1.

Опр. События называются равновероятными (равновозможными), если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.

Опр. Событие 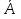, состоящее из тех и только тех элементарных исходов опыта, которые не входят в А, называется противоположным событию А. Вероятности противоположных событий связаны равенством:

.

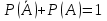Опр. Объединением событий А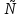В – событие, состоящее из элементарных исходов, благоприятствующих хотя бы одному из событий А, В.

Опр. Пересечение событий А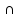В – событие, состоящее из элементарных исходов, благоприятствующих обоим событиям А и В.

Классическая вероятностная схема

Для нахождения вероятности события А при проведении некоторого опыта следует:

1. Определить, что является элементарным событием (исходом) в данном случайном эксперименте (опыте).

2. Найти общее число элементарных событий N.

3. Определить, какие элементарные события благоприятствуют интересующему нас событию А, и найти их число N(A). (Событие можно обозначить любой буквой.)

4. Найти вероятность события А по формуле .

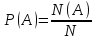Пример 1. Вася, Петя, Коля и Леша бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должен будет Леша.

Решение. Элементарное событие в этом эксперименте – участник, который выиграл жребий. Перечисляем их:

(Вася), (Петя), (Коля), (Леша)

Общее число элементарных исходов N равно 4.

Событию А={жребий пал на Лешу} благоприятствует только одно элементарное событие (Леша). Поэтому N(A)=1. Тогда

Ответ: 0,25.

Пример 2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно 1 раз.

Решение. Орел обозначим буквой О. Решку – буквой Р. В описанном эксперименте могут быть следующие равновозможные элементарные исходы:

ОО, ОР, РО и РР.

Значит, N=4.

Событию А = {выпала ровно одна решка} благоприятствуют элементарные события ОР и РО. Поэтому N(A)=2. Тогда

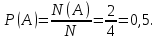
Ответ: 0,5.

Пример 3. В случайном эксперименте бросают две игральные кости. Найти вероятность того, что в сумме выпадет 6 очков.

Решение. Элементарный исход в этом опыте – пара чисел. Первое число выпадает на первой кости, а второе – на второй. Множество элементарных исходов удобно представить таблицей. Строки соответствуют результату первого броска, столбцы – результату второго броска. Всего элементарных событий N=6²=36.

	1	2	3	4	5	6
1					*
2				*
3			*
4		*
5	*
6

Поставим * в ячейках, где сумма равна 6. Таких ячеек 5. Значит, событию А = {сумма очков равна 6} благоприятствует 5 элементарных исходов, т.е N(A)=5. Поэтому,

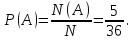
Ответ: .

В следующих задачах явно выписывать все элементарные исходы сложно, но достаточно легко подсчитать их количество.

Пример 4. В среднем из 1000 аккумуляторов, поступивших в продажу, 7 неисправны. Найти вероятность того, что один купленный аккумулятор окажется исправным.

Решение. Элементарный исход – случайно выбранный аккумулятор. Поэтому N=1000.

Событию А = {аккумулятор исправлен} благоприятствует 1000 - 7=993 исхода. Поэтому N(A)=993. Тогда

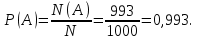
Ответ: 0,993.

Пример 5. В группе иностранных туристов 51 человек, среди них два француза. Для посещения маленького музея группу случайным образом делят на три подгруппы, одинаковые по численности. Найдите вероятность того, что французы окажутся в одной подгруппе.

Решение. В каждой подгруппе 17 человек. Присвоим французам номера – первый и второй. Будем считать, что первый француз уже занял место в какой-то подгруппе (назовем ее подгруппа А). Нужно найти вероятность того, что второй француз оказался в той же подгруппе А.

Для второго француза остается N=50 мест, из них в подгруппе А N(A)=16 мест. Размещение туристов, по условию, случайно, значит, комбинации равновозможны. Поэтому вероятность того, что второй турист попадет в подгруппу А, равна

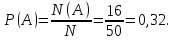
Ответ: 0,32.

Пример 6. Какова вероятность того, что случайно выбранное натуральное число от 82 до 96 делится на 6?

Решение. Общее число элементарных исходов N=15 (количество чисел от 82 до 96). Событию А={выбранное число делится на 6} благоприятствует N(A)=3 исхода (84, 90, 96). Тогда

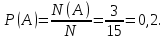
Ответ: 0,2.

Пример 7. На семинар приехали 4 ученых из Норвегии, 2 из Испании и 6 из Италии. Порядок докладов определяется жеребьевкой. Найти вероятность того, что одиннадцатым окажется доклад ученного из Италии.

Решение. Задачи данного типа можно решить по формуле Баесса, но достаточно принять равновозможным порядок докладов и тогда вероятность не будет зависеть от того кто в какой день делает доклад.

Общее число исходов N=12. Число исходов N(A), благоприятствующих событию А={доклад ученного из Италии} равно 6.

Тогда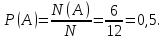

Ответ: 0,5.

Пример 8. Вероятность того что новая шариковая ручка пишет плохо (или не пишет), равна 0,05. Покупатель в магазине выбирает одну новую ручку. Найти вероятность того, что эта ручка пишет хорошо.

Решение. Определим событие:

А={выбранная ручка пишет хорошо}.

Известна вероятность противоположного события:

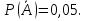
Используя формулу вероятности противоположного события:

P(A)=1-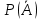=1-0,05=0,95.

Ответ: 0,95.

Пример 9. Перед началом волейбольного матча судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда «Байкал» по очереди играет с командами «Амур», «Енисей», «Вилюй» и «Иртыш». Найти вероятность того, что ровно в двух матчах право владеть мячом выиграет команда «Байкал».

Решение. Пусть 1 – команда «Байкал» владеет мячом первая, 0 – не владеет мячом. Первая комбинация во всех играх 1111, т.е во всех играх «Байкал» первый. Вторая комбинация 1110, т.е «Байкал» в первых трех играх первый.

Итого:

Всего исходов – 16, из них благоприятных – 6.

Вероятность данного события

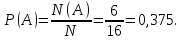
Ответ: 0,375.

Теоремы сложения и умножения вероятностей

Теорема сложения вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

P(A+B)=P(A)+P(B).

Пример 10. На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,1. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к двум темам, нет. Найти вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение. События А= {вопрос на тему «Тригонометрия»} и В={ вопрос на тему «Внешние углы»} несовместны. Тогда P(A+B)=P(A)+P(B)=0,1+0,15=0,25.

Ответ: 0,25.

Пример 11. Найти вероятность того, что при броске игрального кубика выпадет 2 или 5.

Решение: События А= {выпадет 2} и В={ выпадет 5} несовместны. Поскольку Р(А)=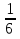 и Р(В)=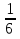, тогда P(A+B)=P(A)+P(B)=.

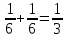Ответ: .

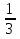Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

P(A+B)=P(A)+P(B) – Р(АВ).

Пример 12. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решeние. Рассмотрим события

А = кофе закончится в первом автомате,

В = кофе закончится во втором автомате.

Тогда

A·B = кофе закончится в обоих автоматах,

A + B = кофе закончится хотя бы в одном автомате.

По условию P(A) = P(B) = 0,3; P(A·B) = 0,12 .

События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:

P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48.

Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52.

Ответ: 0,52.

Опр. События А и В называются независимыми, если появления одного из них не влияет на вероятность появления другого.

Теорема умножения для независимых событий. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

.

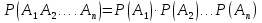Пример 13. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найти вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлить до сотых.

Решение. В этой задаче предполагается, что результат каждого следующего выстрела не зависит от предыдущих. Поэтому события {попал при первом выстреле}, {попал при втором выстреле} и т.д. независимы. Вероятность каждого попадания равна 0,8. Значит, вероятность каждого промаха равна 1 – 0,8=0,2. Воспользуемся формулой умножения вероятностей независимых событий. Получаем, что событие А={попал; попал; попал; промахнулся; промахнулся} имеет вероятность

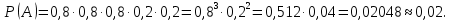
Ответ: 0,02.

Формула полной вероятности

Теорема. Вероятность событии А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) 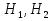, образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:

, (*)

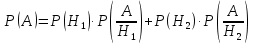где .

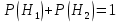Равенство (*) называют формулой полной вероятности.

Пример 14. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая – 55%. Первая фабрика выпускает 5% бракованных стекол, а вторая – 3%. Найти вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Решение. Событие А={купленное стекло окажется бракованным}. Гипотезы Н₁={стекло с первой фабрики}, Н₂={стекло со второй фабрики} образуют полную группу поскольку для Р(Н₁)=0,45 и Р(Н₂)=0,55 суммарная вероятность равна 1.

Условные вероятности 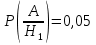, 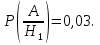Тогда

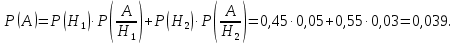
Ответ: 0,039.

Пример 15. В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок производит один выстрел из наудачу взятой винтовки.

Решение. Событие А={мишень будет поражена}. Гипотезы Н₁={винтовка с оптическим прицелом}, Н₂={ винтовка без оптического прицела} образуют полную группу поскольку для Р(Н₁)=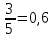 и Р(Н₂)= 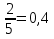суммарная вероятность равна 1.

Условные вероятности 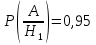, 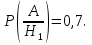Тогда

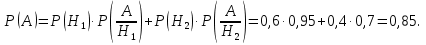
Ответ: 0,85.

Формула Бернулли

Пусть рассматриваются независимые испытания, в каждом из которых вероятность появления события одинакова.

Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0<p<1), событие наступит ровно k раз (безразлично в какой последовательности), равна

,

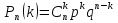где 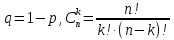–число сочетаний.

Пример 16. Биатлонист попадает в мишень с вероятностью 0,9. Он стреляет пять раз. Найти вероятность того, что он:

А) попадет все пять раз;

В) попадет ровно один раз;

С) не попадет в мишень ни одного раза.

Решение.

А) Согласно формуле Бернулли при k=5 и q=0,1 имеем:

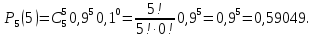
В) При k=1 имеем

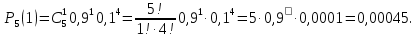
С) При k=0 имеем

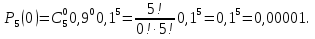
Ответ: 0,59049; 0,00045; 0,00001.

Список литературы

1. А.Г. Мордкович. События. Вероятности. Статистическая обработка данных: доп. Параграфы к курсу алгебры 7-9 кл. общеобразоват. Учреждений / А.Г. Мордкович, П.В. Семенов. – 6-е изд. М.: Мнемозина, 2009. – 112 с.: ил.

2. Математика. Методический журнал для учителей математики. Издательский дом «Первое сентября», январь 2012.

3. Е.А. Бунимирович, В.А. Булычев. Вероятность и статистика в курсе математики общеобразовательной школы. 1-4 лекции. М.: Педагогический университет «Первое сентября», 2011. – 128 с.

4. Е.А. Бунимирович, В.А. Булычев. Вероятность и статистика 5-9 кл.: Пособие для общеобразоват. учеб. Заведений. – М.: Дрофа, 2002. – 160 с.: ил.