Система работы по изучению метрической системы мер на уроках математики в специальной школе VIII вида.
Волгоград 2011 СОДЕРЖАНИЕ: I. Информационно — справочные сведения об опыте. _____________3 II. Технологические сведения об опыте. ________________________ 4 1. Актуальность опыта. __________________________________ 4 2. Задачи, решаемые в опыте. ______________________________ 5 3. Педагогические средства, представленные в опыте. _________ 5 4. Технология опыта. _____________________________________ 6 5. Результативность опыта. ________________________________18 III. Перспективы использования опыта в массовой педагогической практике. _________________________________________________ ___19 1. Условия функционирования опыта. _______________________ 19 2. Теоретико — практические основы опыта. ___________________ 20 3. Перспективы и возможности использования опыта в массовой общеобразовательной практике. ___________________________ 21 Список литературы. __________________________________________ 22 Приложения. I. Информационно- справочные сведения об опыте. Тема опыта: Система работы по изучению метрической системы мер (на уроках математики во вспомогательной школе V111 вида). Автор опыта:Гончарова Светлана Алексеевна. Должность автора опыта: Учитель математики. Место функционирования опыта: ГКС(к)ОУ «Котовская специальная (коррекционная) общеобразовательная школа-интернат VIIIвида»
Адрес:<metricconverter productid=«403805, г» w:st=«on»>403805, г. Котово, Волгоградская обл., ул. Чапаева, д.3, телефон: (84455)4-11-93. Разновидность опыта:Эвристический. Опыт представлен и описан следующими приложениями: Приложение №1: Мониторинг уровня сформированности знаний и умений по теме «Метрическая система мер» уч-ся 5-а класса. Приложение № 2: Алгоритмы, используемые в работе с именованными числами. II. Технологические сведения об опыте. 1. Актуальность опыта. Известно, что математика один из самых трудных предметов для учащихся с интеллектуальной недостаточностью. Это объясняется, с одной стороны, особенностями усвоения математических знаний учащимися, с другой стороны абстрактностью математических понятий. В специальной школе VIII вида уже с первого класса учащиеся знакомятся с единицами измерения. И, в дальнейшем, из года в год, они повторяют имеющиеся у них знания и получают новые, вплоть до девятого класса. Но, несмотря на это, к пятому классу большинство детей не имеют необходимых знаний и умений по данной теме или допускают различные ошибки: ● Нет реальных представлений о величине измерения одной и той же системы мер (см с дм и м) и различных систем мер (м с м, км с кг); ● трудности при установлении соотношения мер; ● При выполнении арифметических действий с числами, полученными при измерении, не принимают во внимание наименования: (7кг+30г= 37кг); переставляют местами разные по величине меры (40см 3м); производят неправильную запись наименований, т.е. Возможность выразить в более крупной единице (4км 291 см=42 м 91см) ● Неточность измерений, неумение выбрать соответствующую единицу измерения, правильно назвать или записать результат измерения простым или составным именованным числом. Причины перечисленных трудностей и ошибок кроются в особенностях познавательных и психофизических процессов развития учащихся специальной школы VIII вида. Но на все перечисленные трудности, нельзя отрицать значимость и необходимость изучения данной темы, которая позволяет тесно связать математические знания с жизнью, уч-ся получают практические умения и навыки измерения, необходимые как в повседневной жизни, так и при овладении будущими профессиями. В данном опыте представлена система работы по изучению единиц измерения длины и массы, которая дает возможность показать практическую значимость темы, делает процесс запоминания непринужденным, интересным и прочным, способствует формированию обобщений, развитию целенаправленности действий. Практически все учащиеся хорошо усваивают данную тему. 2. Задачи, решаемые в опыте. В опыте решаются следующие задачи: ● Разработать систему работы по изучению чисел, полученных при измерении; ● Разработать наиболее оптимальные приемы и средства работы, которые бы сделали процесс обучения доступным и эффективным; ● Пробудить интерес к урокам математики всех учащихся, показав значимость изучение данной темы ● Представить результаты эффективности применения данной системы работы над числами, полученными при измерении. 3. Педагогические средства, представленные в опыте. Представлены, следующие педагогические средства: ● система вопросов, заданий к данной теме изучения; ● памятки алгоритмы; ● описание жестов, помогающие прочно запомнить единицы измерения длины; ● игры, физ. минутки закрепляющие полученные знания; ● познавательные и занимательные задачи, позволяющие показать значимость изучения данной темы, и применить полученные знания на практике, в новой ситуации; 4. Технология опыта. Принимая во внимание все перечисленные трудности в обучении детей с интеллектуальной недостаточностью, необходимо привести высказывание Л.С. Выготского о том, что «дети с дефектом могут достигнуть то же, что и нормальные, но иным способом, на ином пути, иными средствами, и для педагога очень важно знать своеобразие пути, по которому он должен повести ребенка». В его же трудах мы находим и описание этапов овладения новыми знаниями, следуя которым, можно успешно решать проблемы в обучении и коррекции личности умственно отсталого ребенка. Вот эти этапы: I этап. Мотивация (создание жизненной ситуации, которую необходимо решить, т.е. предварительное представление о задании); II этап. Действия с предметами (включение всех уч-ся класса в предметно- практическую деятельность, в результате которой ребята «открывают» новые знания) III этап. Внешняя речь (освоение действий в плане громкой речи, когда выполняется задание, и каждый шаг подробно объясняется). Активизация всех анализаторов: введение жестов, символов, графических обозначений, алгоритмов. IV этап. Внутренняя речь (перенос действий в умственный план, задание выполняется самостоятельно, с опорой на полученное правило, алгоритм). Особенности обучения построенного в соответствии с перечисленными этапами является то, что знания не даются в готовом виде, дети их «открывают» сами в процессе активной практической деятельности, решая жизненно значимую ситуацию, а значит знания, полученные таким образом, более осознанные и прочные. В данном опыте рассмотрена система работы по изучению единиц измерения длины и массы в соответствии с перечисленными этапами Основные этапы работы при изучении метрической системы мер. 1. Накопление (активизация, расширение или уточнение) чувственного опыта, необходимого для понимания смыслового содержания изучаемых величин, связи между величинами составного именованного числа, в процессе выполнения действий с этими числами, с измерительными инструментами (и без них), а также для речевого оформления производимых действий. 2. Введение понятия семантика слова, жестовая символика, графическое обозначение. 3. Числовое оформление данного понятия: простые и составные именованные числа, преобразование именованных чисел (замена мелких мер крупными и наоборот); соотношение между единицами измерений одной метрической системы. 4. Действия с именованными числами (сложение, вычитание); действия с именованными и отвлеченными числами (умножение и деление). Проводя первые уроки по теме «Именованные числа» я, к сожалению, убедилась в том, что большинство учащихся 5 класса не имеют реальных представлений о единицах измерения длины, с которыми они познакомились в начальной школе; не помнят и о соотношениях между этими мерами. Поэтому, прежде чем переходить к действиям с именованными числами, я провела ряд занятий на повторение ранее изучаемого материала, опираясь на практический опыт своих учеников. Метр. С этой мерой длины школьники знакомятся в 3 классе, повторяют в четвертом и, по логике вещей, должны иметь четкие представления об этог' единице измерения. На практике выходит иная ситуация. Вот пример. Приношу на урок ленту, бичевку, веревку и предлагаю следующий вопрос: — Как узнать длину ленты? (Надо измерить.) – Чем будем мерить? (Линейкой) – В каких единицах запишем ответ? (Молчание) Вывод: у учащихся сформировано представление о необходимости выполнить измерительные действия. Однако большинство из них забыли как называются единицы измерения длины и как они записываются на письме. Понятие (слово) не подкреплено действием (жестом), символом. Для активизации памяти предлагаю измерить длину класса: — Чем будем мерить длину? (Линейкой) — А есть ли другой инструмент? (Метр — большая деревянная линейка). Словарная работа. МЕТР В этот момент ставлю перед собой две задачи: 1. Подкрепить новое понятие практической деятельностью детей. 2. Довести до сознания учащихся, что метр — это определенное расстояние, протяженность. — Ребята, у нас в классе только один деревянный метр, а вас 8 человек (т.е. создаю проблемную ситуацию). Что надо сделать, чтобы в работе принимали ученики всего класса? Решить эту проблему предлагаю 2 способами: 1 способ. Раздаю всем детям заранее приготовленные полоски плотной бумаги длиной в 1м. Проводим с детьми измерение. По окончанию работы подводим итог: а) длину класса (и не только) можно измерить с помощью любого предмета, длина которого соответствует длине деревянного метра; б) этот способ не совершенен, т.к. предлагает использование предмета, который не всегда оказывается под рукой. Таким образом, подвожу детей ко 2 способу. Предлагаю еще раз внимательно рассмотреть метр и сравнить его с собой. В результате этой работы, учащиеся сравнивают метр с расстоянием от плеча до кончиков пальцев вытянутой руки. Самостоятельно делают выводы: метр есть у каждого из нас, его можно показать на себе, этим метром можно производись измерительные действия. (Производим практические измерительные действия с веревкой, бичевкой, резинкой и др. предметами). Систематизацию и закрепление полученных знаний провожу по таблице «Единицы измерения длины». (см. Приложение 7.) Есть еще один момент в работе с единицами измерения на данном этапе: необходимо довести до сознания детей, что все меры, которые мы показываем на себе, являются приближенными, но это не ошибка, это жизненная необходимость. Дециметр. Понятие «дециметр» отрабатывается по аналогии с понятием «метр». Создаю ситуацию «успеха»: предлагаю измерить ленту, бант, веревку. Длина этих предметов равна целому числу метров. Создаю проблемную ситуацию: предлагаю измерить парту. Ученики пользуются метром или меркой своего тела — получается остаток. Делаем вывод: не все предметы можно измерить метром, есть другие единицы измерения длины, которые меньше метра, эти единицы помогут нам вычислить остаток. Ввожу понятие «дециметр». Еще раз измеряем парту, получаем результат: 1м 2дм. Ставлю перед учащимися новую задачу: — Метр в классе один, вас -8 человек, каким способом можно измерить парты класса всем одновременно? Такими вопросами подвожу детей к мысли о том, что необходимо эту меру длины найти на себе: рассматриваем деревянный метр, определяем количество делений, режем метровые бумажные ленты на 10 частей, сравниваем эти бумажные эквиваленты дециметра со своим телом, приходим к выводу: дециметр равен ширине ладони. Словарная работа ДЕЦИМЕТР Краткое обозначение на письме: дм Соотношение: 1м = 10дм Закрепление по таблице «Единицы измерения длины» (см. Приложение 7) Аналогично провожу работу над понятием «сантиметр» и «миллиметр». Перед тем как проводить урок по теме «километр», веду учащихся на экскурсию, где они реально увидят расстояние в 1км, пройдут это путь, сами. установят связь между расстоянием в 1км и временем, необходимым, чтобы пройти это расстояние. В дальнейшем, используя отработанную схему проведения уроков, учащиеся легко запоминают само понятие «километр», его обозначение на письме, графический символ, жест (см. Приложение 7) Особое внимание на этом этапе работы уделяю заучиванию соотношений между единицами измерения длины: сколько в крупной мере мелких мер. Заучивание идет достаточно трудно. Для более легкого запоминания использую деятельностный прием «отстукивание» (отхлопывание). Приведу пример. Игра «Молчанка» Цель: изучение соотношения мер длины. Содержание: «Вы немые. Вместо языка говорят ваши руки». Вопрос: Сколько в 1м — см? Ответ:(100см) — ученики делают два стука по парте в соответствии с количеством нулей. Вопрос: Сколько в 1км — м? Ответ: (1000м) — три стука. Вопрос: Сколько в 1дм — см? Ответ: (10см) — один стук. И т. д. Эту игру можно проводить и с использованием внешней речи, т.е. с проговариванием своих действий. В результате такой работы дети с 'интеллектуальной недостаточностью хорошо усваивают необходимые знания. После того, как все понятия уточнены, провожу работу по их закреплению. Для этой цели использую ряд приемов: 1. Физминутки (см. Приложение №6) 2. Сюжетно — ролевые игры, игры — пантомимы, игры — соревнования (см. Приложение № 5) 3. Слуховой, зрительный математический диктант. 4. Ввожу в устный счет занимательные задания типа: Что длиннее 1км или 1см? Какая стена класса короче? Как, без использования инструментов, измерить доску? И др. 5. Практические упражнения на уроке: — выполнить измерение с использованием инструментов; — выполнить измерения без использования инструментов (использовать мерки тела); — определять расстояние (длину, размер) на глаз. 6. Письменные упражнения на доске, в тетради: — начертить единицы измерения длины с помощью инструментов; без инструментов. 7.Задачи познавательного и занимательного содержания. (Приложение № 8). *■'
Единицы измерения массы. Перед проведением занятий по теме «Меры массы», веду учащихся на экскурсию в школьную столовую, где в подсобных помещениях расположены различных видов весы, разновесы. Школьники знакомятся с ними, включая в работу все анализаторы: слух, зрение, тактильные и мускульные ощущения. В дальнейшем на занятиях повторяем меры «килограмм» и «центнер», и вводим новые понятия «грамм» и «тонна». Работа по каждому понятию проводится отдельно. В основе учения каждого понятия лежит действие с предметами. Начинаю повторять меры массы с понятия «КИЛОГРАММ». Ход урока. 1. Приношу ряд предметов: булка хлеба, пачка сахара, зерно пшеницы, гантели весом в 1кг, 5кг, весы. 2. Предлагаю, опираясь на чувственный опыт, ответить на вопрос: — Какие из предложенных здесь предметов весят один килограмм? 3. Предлагаю всем учащимся подержать на руке гирю массой 1кг, с тем, чтобы мускульно ощутить меру массы равную килограмму. 4. На одну руку кладу килограммовую гирю, на противоположную — пачку сахара. Предлагаю самостоятельно сделать выводы. 5. Возвращаюсь ко второму пункту, предлагаю отобрать предметы весом 1кг. 6. Словарная работа килограмм 7. Запись в тетради. 8. Практическая работа по отвешиванию и взвешиванию предметов, весом 1кг. Грамм. С этой единицей измерения массы знакомятся впервые. Создаю жизненную ситуацию, в которой бы ученики почувствовали необходимость в более мелкой единице массы. — Сколько ложек сахара вы кладете в стакан чая? Какова масса этого сахара? Сколько нужно пакетиков, чтобы заварить один стакан чая? Какова масса этого пакетика? Учащиеся затрудняются ответить, однако им становиться очевидно, что с помощью гири в 1кг нельзя определить массу сахара или пакетика чая, эта слишком большая мера. Из жизненного опыта, из представлений, полученных на экскурсии, учащиеся припоминают, что есть другие гири, которые измеряют предметы массой меньше 1кг. Ввожу понятие ГРАММ Предлагаю рассмотреть, ощутить гирю массой в <metricconverter productid=«1 г» w:st=«on»>1 г. Закрепляю действие жестом, словом: легко или тяжело. Даю возможность сравнить: гиря массой 1кг и гиря массой в 1г. Дети делают соответствующие выводы. Предлагаю определить массу предметов, лежащих на столе. Опыт показал: все предметы, которые меньше и легче одного килограмма, ученики приводят в пример, как предметы массой 1г. Чтобы исключить подобные ошибки, знакомлю учеников с другими разновесами: 5г, 10г, 20г, 50г, 100. 200г, 500г. На этом этапе провожу практическую работу по взвешиванию различных предметов. Соотношение между килограммом и граммом ученики устанавливают сами: гирю в 1кг они уравновешивают на весах другими гирями и подсчитывают, сколько потребовалось граммов. Таким образом, они устанавливают соотношение: 1кг = 1000г Центнер. Чтобы вспомнить, что такое «центнер» предлагаю еще одну экскурсию к столовую. Измеряем массу мешков с картофелем на специальных весах. Выясняем, что масса одного мешка приблизительно равна <metricconverter productid=«50 кг» w:st=«on»>50 кг, предлагаю поднять мешок с картофелем, чтобы мускульно ощутить массу равную <metricconverter productid=«50 кг» w:st=«on»>50 кг Предлагаю ученикам решить задачу: «Масса одного мешка с картофелем равна 50кг. Чему равна масса двух таких же мешков с картофелем?». Деть правильно находят решение задачи, получают 100кг. Ставим на весы второй такой же мешок с картофелем, получаем 100кг. Вновь предлагаю поднять этот вес. Навалившись всем классом, они приподнимают эти мешки с картофелем, тем самым мускульно ощущают эту меру массы. Теперь я твердо убеждена, что мои ученики не спутают такие меры как килограмм, грамм и центнер. Уже на занятиях, ввожу понятие ЦЕНТНЕР, осуществляю словарную работу. Выясняем, что 100кг это то же самое, что 1ц. Дети самостоятельно выводят соотношения мер: 1ц = 100кг. Предлагаю своим ученикам запомнить эту картинку и в дальнейшей работе пользуюсь ею. Тонна. Использовать практическую деятельность при изучении этой меры массы невозможно. При изучении понятия «тонна» использую метод припоминания, т.е. вызываю у детей конкретные образы предметов, масса которых превышает 1 центнер. Таким образом, я материализую понятие, делаю его конкретным, связывая с реальным предметом. Так например,, предлагаю рассмотреть картинку, где изображена машина на весах, масса которой <metricconverter productid=«1000 кг» w:st=«on»>1000 кг. Ученики самостоятельно приходят к выводу, что машина весит <metricconverter productid=«1000 кг» w:st=«on»>1000 кг, а <metricconverter productid=«1000 кг» w:st=«on»>1000 кг = 1т. Ввожу понятие ТОННА провожу словарную работу, предлагаю игровой материал для закрепления(см. Приложение №5) Соотношение мер «тонна- килограмм», «тонна- центнер» дети делают самостоятельно. Для закрепления темы «Соотношение мер массы» использую прием «отстукивания» (отхлопывания) по аналогии с мерами длины. Преобразование чисел, полученных при измерении. Это обязательный этап в работе с именованными числами, проводится каждый раз перед выполнением действий с ними. Этот вид работы предполагает, что учащиеся должны: а) знать названия мер, умело ими оперировать; б) знать соотношения между единицами одной метрической системы; в) уметь производить два действия — умножение и деление — на 10, 100 и 1000 (с остатком и без него). Приемы, используемые в работе по преобразованию именованных чисел 1. Постановка учебной цели. Создаю на уроке жизненную проблемную ситуацию, при решении которой учащиеся должны убедиться в необходимости преобразования именованных чисел. а) из крупных мер в мелкие (раздробление): «У меня в руках полоска бумаги длиной 1дм. Я отрезаю 15см. Какой длины полоска осталась?» б) из мелких мер в крупные (превращение): «Я пошла в магазин за продуктами. Кассир дал мне сдачу 300к (показываю учащимся). Вы видите, это целый мешок денег. Он тяжелый, не помещается в кошелек. Что же мне нужно сделать?» 2. Организация учебных действий. а) Предлагаю учащимся самостоятельно отрезать от полосы бумаги 15см. Задаю вопросы: — Какой длины полоска была? — Сколько отрезали? — Какой длины полоска осталась? В результате проведенной работы, учащиеся приходят к выводу: надо заменить 1м сантиметрами. Теперь можно ответить на поставленный вопрос. 3. Первичное закрепление с комментированием. Ввожу алгоритм действий (см. Приложение №4)/ а) Зная соотношение мер длины, учащиеся запоминают 1м = 100см. Устно выполняют вычисления и получают ответ: — Осталась полоска длиной 85см. Для письменной работы предлагаю другое упражнение: Зм =… см (первичное закрепление проводит учитель, опираясь на алгоритм действия, используя прием «отстукивания») 1. — Проверим есть ли пропущенные разряды. В одном метре <metricconverter productid=«100 сантиметров» w:st=«on»>100 сантиметров. Это два нуля. Постучите, (дети отстукиваю; количество нулей) Приписываем пропущенные разряды справа, получаем следующую запись: 3м 0 0см 2. — Заменим крупные меры мелкими. Предлагаю учащимся закрыть ладонью (пальчиком) крупную меру и переписать оставшееся число и наименование без изменений: 3м 0 0см= 300см. Вывод: Крупную меру заменили мелкой. При выполнении письменных действий использую последний пункт алгоритма действий и метод «волна». 3. — Заменим мелкую меру крупной. а) В одном метре сто сантиметров. «Чтобы разделить число на 100, надо отбросить справа два нуля»: 3ØØ см б) — Чтобы в тетрадях не было зачеркиваний, я буду использовать «волну»: обведу волнистой линией столько цифр, сколько надо отбросить: 300см в) — Все, что стрит впереди «волны» — это крупная мера, остальные цифры — мелкие меры: 3м 0 0см 4. Самостоятельная работа. А) по вариантам использование алгоритма Б) в парах действий 5. Проведение тренировочных упражнений. Сильные учащиеся выполняют задание по учебнику самостоятельно. Учащиеся, которые занимаются по программе со сниженным уровнем требований — работают у доски, под контролем учителя. Вся работа по преобразованию именованных чисел строится с учетом постепенного усложнения материала: от более легких случаев — к более сложным: Действия с именованными числами. Действия над числами, полученными от измерения величин. Выполняются так же, как действия над многозначными числами, с той лишь разницей, что при числах должны быть записаны наименования единиц измерения. Действия над числами, полученными от измерения величин, опираются не знания учащимися единиц измерения и их соотношение, а также умение выразить одни меры другими. Обучая учащихся выполнять действия сложения, вычитания, умножения и деления, придерживаюсь следующих правил: 1. Каждое действие объясняю, включив всех учащихся в предметно- практическую деятельность и создав жизненную необходимую ситуацию. 2. Вся работа строится в соответствии с алгоритмом действий (см. Приложение №4) 3. У именованного числа должно быть два наименования: впереди — крупная мера, затем мелкая. Если дано одно наименование, дополняю его вторым, в зависимости от соотношения мер. 4. Работа строится с учетом постепенного усложнения материала: от простых случаев к сложным. 5. Результативность опыта. Таким образом, в данном опыте получен следующий результат. Изучая метрическую систему мер, действия с именованными числами, их преобразование, учебный процесс строился на активной познавательной деятельности учащихся, которые получали новые знания не в готовом виде, а «открывали» их сами в процессе выполнения действий с предметами под контролем учителя. В конце каждой четверти, в 5-а классе проводила контрольный срез по данной теме (см. Приложение № 1), я убедилась, что уч-ся получили прочные знания о мерах длины и массы. Можно отметить повышение активности, появился интерес к предмету. В ходе урока принимали участие как сильные, так и слабые учащиеся. Такие приемы запоминания ед. измерения как жестовый, а соотношение единиц измерения, как простукивание хорош еще и тем, что дает возможность активизировать все анализаторы, а значит повысить качество усвоения и запоминания нового материала. А так же позволяет легко припомнить полученные знания в нужный момент, стоит показать и они «всплывают» в памяти, в сознании ребенка. Вывод: Предложенная система работы над числами, полученными при измерении эффективна при обучении учащихся с интеллектуальной недостаточностью. III. Перспективы использования опыта в массовой педагогической практике. 1. Условия функционирования опыта. Опыт функционирует в ГОУ «Котовская специальная /коррекционная/ общеобразовательная школа- интернат VIII вида». Продолжительность уроков в данной школе – 40 минут, самоподготовки нет. Во второй половине дня ребята посещают факультативные занятия, кружки, секции. Уроки проводятся в кабинете математики для 5-9 классов со стандартным набором инвентаря и приспособлений. В классе имеется необходимый материал для уроков математики, опорные таблицы, алгоритмы, схемы к задачам, опросники по всем темам, дидактический материал, измерительные инструменты, макеты геометрических фигур, дополнительная литература по предмету. Занятия по предмету проходят в одну смену. Учащиеся обучаются по программе специальных (коррекционных) образовательных учреждений VIII вида. В 5-а классе 8 учащихся: 4 мальчика и 4 девочки. Класс по знаниям «средний»: 4 ученика занимаются по основной программе 5-го класса хорошо, 3 ученика — удовлетворительно, один ученик занимается по программе с заниженными требованиями по основным предметам. По особенностям познавательной деятельности, работоспособности, состояния внимания и поведения состав учащихся разделен на группы: 1. Дети с неосложненной формой олигофрении: Дмитрий К., Кристина Ш. Екатерина Р. Александр К. Елизавета Б. 2. Дети-с отклонениями в здоровье, характеризующиеся неустойчивостью эмоционально- волевой сферы с преобладанием процесса торможения: Татьяна Б. Артем П. Классный коллектив находится на стадии формирования. Взаимоотношения между ребятами доброжелательные. Основная группа ребят хорошо поддается педагогическому влиянию. Все ребята посещают факультативные занятия по математике, которые проходят один раз в неделю (2 часа), а так же посещают кружки и секции. Автор опыта имеет высшее образование, по специальности олигофренопедагогика. В данной школе работает 9 лет. На протяжении своей педагогической деятельности принимала активное участие в районных МО, областных семинарах на базе своего учреждения, в педагогических и методических советах школы, является руководителем МО учителей естественно- математического цикла шестой год, активно занимается самообразованием. 2. Теоретико- практические основы опыта. Данный опыт опирается на традиционную методику обучения математике, представленную В.В. Эк и М.Н. Перовой, на исследования Л.С. Выготского в области психологии и собственные авторские разработки приемов и средств обучения. 3. Перспективы и возможности использования опыта в массовой общеобразовательной практике. Данный опыт может быть полезен учителям математики и начальных классов специальных (коррекционных) школ VIII вида и средних общеобразовательных школ. Рекомендации будущим пользователям опыта. Последователям опыта рекомендую учесть следующее: 1) Чтобы научить детей с интеллектуальной недостаточностью метрической системе мер; преобразованию именованных чисел и действий с ними, надо создать жизненную ситуацию и включить всех учащихся класса в предметно- практическую деятельность, в результате чего учащиеся увидят необходимость изучения данного материала; 2) Работая над новым материалом, следовать по строго установленным этапам действий. Работу вести систематически из урока в урок, из класса в класс. Желательно начинать с начальных классов. 3) Закрепление знаний по данной теме и умений производить на уроках математики, на других учебных предметах, особенно на уроках трудового обучения, при работе на пришкольном участке. Успех здесь зависит от целенаправленной работы всех учителей и воспитателей, работающих с коллективом учащихся.
ЛИТЕРАТУРА. 1. Л.С. Выготский, «Основы дефектологии» т.4, т.5 Москва «Педагогика», 1984. 2. М.Н. Перова, Методика преподавания математики во вспомогательной школе. Москва, «Просвещение», 1989. 3. М.Н. Перова, Дидактические игры и упражнения во вспомогательной школе. Москва, «Просвещение», 1975. 4. В.В. Эк, Обучение математике учащихся младших классов вспомогательной школы. Москва, «Просвещение», 1990. 5. Программы для 5-9 классов специальных (коррекционных) общеобразовательных учреждений VIII вида: СБ.1.-М.: Гуманит. Изд. Центр, ВЛАДОС, 200. 6. М. Волович «Как успешно обучать математике». Приложение к газете «Первое сентября», «Математика» №3,6,8,10, 12 за <metricconverter productid=«1997 г» w:st=«on»>1997 г. 7. Обучение детей с нарушениями интеллектуального развития: (Олигофренопедагогика): Учеб. Пособие для студ. Высш. Пед. Учеб. Заведений / под ред. Б.П.Пузанова. — М.: Издательский центр «Академия», 2003.
ПРИЛОЖЕНИЕ № 1 МОНИТОРИНГ УРОВНЯ СФОРМИРОВАННОСТИ ЗНАНИЙ И УМЕНИЙ ПО ТЕМЕ «МЕТРИЧЕСКАЯ СИСТЕМА МЕР» УЧАЩИХСЯ 5 «А» КЛАССА.
ЦЕЛЬ: Проследить и сравнить динамику усвоения знаний и умений по теме «Метрическая система мер» у учащихся 5 «А» класса с интеллектуальной недостаточностью, обучающихся по системе основанной на активном участии ребят в процессе овладения новыми знаниями
ЗАДАЧИ: 1.Проследить динамику усвоения знаний и умений по теме «Метрическая система мер» за год.
2.Проанализировать полученные результаты. 3.Дать оценку эффективности представленной системы работы над темой «Метрическая система мер».
ОБЪЕКТ ИССЛЕДОВАНИЯ: Учебно-воспитательный процесс в 5 «А» классе за 2007-2008 учебный год.
ПРЕДМЕТ ИССЛЕДОВАНИЯ: Условия и факторы препятствующие и стимулирующие формирование знаний о единицах измерения, о их соотношениях, и умений преобразовывать именованные числа и выполнять действия с ними.
ДИНАМИКА УСПЕВАЕМОСТИ ПО ТЕМЕ «МЕТРИЧЕСКАЯ СИСТЕМА МЕР» В 5 «А» КЛАССЕ.
|
№ п.п. |
Ф. И. |
1 четверть |
2 четверть |
3 четверть |
4 четверть |
|
1 |
Борисова Т. |
2 |
2 | 3 | 3 |
|
2 |
Брух Л. |
2 |
3 | 3 | 4 |
|
3 |
Клыков Д. |
3 |
4 | 5 | 5 |
|
4 |
Курин с. |
2 |
3 | 3 | 4 |
|
5 |
Литвинов и. |
3 |
4 | 4 | 5 |
|
6 |
Подин А. |
2 |
2 | 3 | 3 |
|
7 |
Рудомётова К. |
3 |
4 | 4 | 5 |
|
8 |
Швец К. |
3 |
4 | 5 | 5 |
|
Оценка |
1 четверть |
2 четверть |
3 четверть |
4 четверть |
|
«5» |
— |
— |
2 |
4 |
|
«4» |
— |
4 |
2 |
2 |
|
«3» |
4 |
2 |
4 |
2 |
|
«2» |
4 |
2 |
— |
— |
|
«1» |
— |
— |
— |
— |
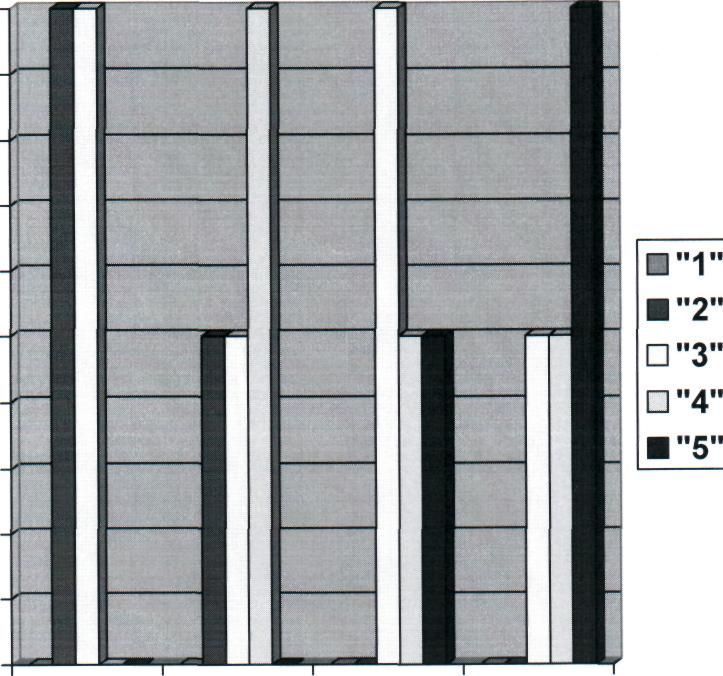
ГИСТОГРАММА УЧЁТА УСПЕВАЕМОСТИ
ПО ЧЕТВЕРТЯМ
Анализ мониторинга уровня сформированности знаний и умений по теме «Метрическая система мер» у учащихся 5 «А» класса. Мониторинг проводился в течение всего 5 класса. Из таблицы и гистограммы, представленных в мониторинге, видно, что описанная система работы над числами, полученными при измерении, позволяет всем ребятам повысить уровень успеваемости и добиться положительных результатов. Шесть учащихся усвоили тему «Метрическая система мер» хорошо и отлично. Двое — удовлетворительно, но это связанно с особенностями их психических процессов.
ВЫВОДЫ: Повышению уровня сформированности знаний и умений по теме «Метрическая система мер» способствуют: 1.Активной познавательной деятельности учащихся, которые получают новые знания не в готовом виде, а «открывают» их сами, в процессе выполнения действий с предметами под контролем учителя. 2.Повышение уровня мотивации учебной деятельности, через: создание жизненных ситуаций, определение значимости изучаемого материала, личный опыт учащихся.
3.Приемы запоминания, которые активизировали бы как можно больше анализаторов.
ПРОБЛЕМЫ:
1.Обучение, некоторых детей, по данной теме, затруднено в силу их диагноза.
2.На изучение темы «Метрическая система мер» по программе отводится недостаточное количество часов.
3.Рассматриваемая тема является одной из самых трудных для учащихся с интеллектуальной недостаточностью.
ОБЩИЕ ВЫВОДЫ:
l. Все поставленные задачи были выполнены. Данный мониторинг показывает эффективность применения описанной системы работы над числами, полученными при измерении.
2.Наряду с положительными результатами есть и недостатки: двое учащихся (Таня Б. и Артем П.) по итогам за год имеют низкий уровень знаний по теме. Причина: учащиеся занимаются по программе с заниженными требованиями. З.В целом работа ведется в правильном направлении.
РЕКОМЕНДАЦИИ НА УЧЕБНЫЙ ГОД.
1.Продолжить работу по данной системе работы с этими же учащимися в 6 классе.
2.Продолжить мониторинговую деятельность по данному направлению. 3.Преемственность в работе по данной теме с учителями начальных классов и трудового обучения.
ПРИЛОЖЕНИЕ № 2. АЛГОРИТМЫ, ИСПОЛЬЗУЕМЫЕ В РАБОТЕ С ИМЕНОВАННЫМИ ЧИСЛАМИ,
АЛГОРИТМЫ.
1. Выражение в более крупных единицах измерения .
1.Определить крупную единицу измерения.
2.Вспомнить: , ,
3.Отделить мелкие единицы. 4, Оставшиеся — крупные единицы.
2. Выражение в более мелких единицах измерения .
1.Вспомнить: .,..,...
2.Проверить, есть ли пропущенный разряд. 3.Закрыть наименование крупных единиц. 4.Выразить в мелких (оставшихся) единицах.
3. Действия с именованными числами.
1.Проверить, есть ли пропущенный разряд
2. Заменить крупные единицы мелкими. 3.Выполнить действие в столбик. 4. Заменить мелкие единицы крупными
![]()
Главная аттестационная комиссия Комитета по образованию Администрации Волгоградской области
Волгоградская государственная академия повышения квалификации и переподготовки работников образования
СИСТЕМА РАБОТЫ ПО ИЗУЧЕНИЮ МЕТРИЧЕСКОЙ СИСТЕМЫ МЕР
НА УРОКАХ МАТЕМАТИКИ В КОРРЕКЦИОННОЙ ШКОЛЕ VIII ВИДА.
Квалификационная работа в форме
описания педагогического опыта соискателя
высшей квалификационной категории
Гончаровой Светланы Алексеевны, учителя
математики ГОУ «Котовская специальная
/коррекционная/ общеобразовательная школа-
-интернат VIII вида».
Волгоград 2008.
СОДЕРЖАНИЕ:
I. Информационно - справочные сведения об опыте. _____________3
II. Технологические сведения об опыте. ________________________ 4
1. Актуальность опыта. __________________________________ 4
2. Задачи, решаемые в опыте. ______________________________ 5
3. Педагогические средства, представленные в опыте. _________ 5
4. Технология опыта. _____________________________________ 6
5. Результативность опыта. ________________________________18
III. Перспективы использования опыта в массовой педагогической практике. ____________________________________________________19
-
Условия функционирования опыта. _______________________ 19
-
Теоретико - практические основы опыта. ___________________ 20
-
Перспективы и возможности использования опыта в массовой общеобразовательной практике. ___________________________ 21
Список литературы. __________________________________________ 22
Приложения.
I. Информационно- справочные сведения об опыте.
Тема опыта:
Система работы по изучению метрической системы мер (на уроках математики во вспомогательной школе V111 вида).
Автор опыта: Гончарова Светлана Алексеевна.
Должность автора опыта: Учитель математики.
Место функционирования опыта: ГКС(к)ОУ «Котовская специальная (коррекционная) общеобразовательная школа-интернат VIII вида»
Адрес: 403805, г. Котово, Волгоградская обл., ул. Чапаева, д.3, телефон: (84455)4-11-93.
Разновидность опыта: Эвристический.
Опыт представлен и описан следующими приложениями:
Приложение №1: Мониторинг уровня сформированности знаний и умений по теме «Метрическая система мер» уч-ся 5-а класса.
Приложение № 2: Алгоритмы, используемые в работе с именованными числами.
II. Технологические сведения об опыте.
1. Актуальность опыта.
Известно, что математика один из самых трудных предметов для учащихся с интеллектуальной недостаточностью. Это объясняется, с одной стороны, особенностями усвоения математических знаний учащимися, с другой стороны абстрактностью математических понятий.
В специальной школе VIII вида уже с первого класса учащиеся знакомятся с единицами измерения. И, в дальнейшем, из года в год, они повторяют имеющиеся у них знания и получают новые, вплоть до девятого класса. Но, несмотря на это, к пятому классу большинство детей не имеют необходимых знаний и умений по данной теме или допускают различные ошибки:
-
Нет реальных представлений о величине измерения одной и той же системы мер (см с дм и м) и различных систем мер (м с м, км с кг);
-
трудности при установлении соотношения мер;
-
При выполнении арифметических действий с числами, полученными при измерении, не принимают во внимание наименования: (7кг+30г= 37кг); переставляют местами разные по величине меры (40см 3м); производят неправильную запись наименований, т.е. Возможность выразить в более крупной единице (4км 291 см=42 м 91см)
-
Неточность измерений, неумение выбрать соответствующую единицу измерения, правильно назвать или записать результат измерения простым или составным именованным числом.
Причины перечисленных трудностей и ошибок кроются в особенностях познавательных и психофизических процессов развития учащихся специальной школы VIII вида.
Но на все перечисленные трудности, нельзя отрицать значимость и необходимость изучения данной темы, которая позволяет тесно связать математические знания с жизнью, уч-ся получают практические умения и навыки измерения, необходимые как в повседневной жизни, так и при овладении будущими профессиями.
В данном опыте представлена система работы по изучению единиц измерения длины и массы, которая дает возможность показать практическую значимость темы, делает процесс запоминания непринужденным, интересным и прочным, способствует формированию обобщений, развитию целенаправленности действий. Практически все учащиеся хорошо усваивают данную тему.
2. Задачи, решаемые в опыте.
В опыте решаются следующие задачи:
-
Разработать систему работы по изучению чисел, полученных при измерении;
-
Разработать наиболее оптимальные приемы и средства работы, которые бы сделали процесс обучения доступным и эффективным;
-
Пробудить интерес к урокам математики всех учащихся, показав значимость изучение данной темы
-
Представить результаты эффективности применения данной системы работы над числами, полученными при измерении.
3. Педагогические средства, представленные в опыте.
Представлены, следующие педагогические средства:
-
система вопросов, заданий к данной теме изучения;
-
памятки алгоритмы;
-
описание жестов, помогающие прочно запомнить единицы измерения длины;
-
игры, физ. минутки закрепляющие полученные знания;
-
познавательные и занимательные задачи, позволяющие показать значимость изучения данной темы, и применить полученные знания на практике, в новой ситуации;
4. Технология опыта.
Принимая во внимание все перечисленные трудности в обучении детей с интеллектуальной недостаточностью, необходимо привести высказывание Л.С. Выготского о том, что «дети с дефектом могут достигнуть то же, что и нормальные, но иным способом, на ином пути, иными средствами, и для педагога очень важно знать своеобразие пути, по которому он должен повести ребенка».
В его же трудах мы находим и описание этапов овладения новыми знаниями, следуя которым, можно успешно решать проблемы в обучении и коррекции личности умственно отсталого ребенка.
Вот эти этапы:
I этап. Мотивация (создание жизненной ситуации, которую необходимо решить, т.е. предварительное представление о задании);
II этап. Действия с предметами (включение всех уч-ся класса в предметно- практическую деятельность, в результате которой ребята «открывают» новые знания)
III этап. Внешняя речь (освоение действий в плане громкой речи, когда выполняется задание, и каждый шаг подробно объясняется). Активизация всех анализаторов: введение жестов, символов, графических обозначений, алгоритмов.
IV этап. Внутренняя речь (перенос действий в умственный план, задание выполняется самостоятельно, с опорой на полученное правило, алгоритм).
Особенности обучения построенного в соответствии с перечисленными этапами является то, что знания не даются в готовом виде, дети их «открывают» сами в процессе активной практической деятельности, решая жизненно значимую ситуацию, а значит знания, полученные таким образом, более осознанные и прочные.
В данном опыте рассмотрена система работы по изучению единиц измерения длины и массы в соответствии с перечисленными этапами
Основные этапы работы при изучении метрической системы мер.
1. Накопление (активизация, расширение или уточнение) чувственного опыта, необходимого для понимания смыслового содержания изучаемых величин, связи между величинами составного именованного числа, в процессе выполнения действий с этими числами, с измерительными инструментами (и без них), а также для речевого оформления производимых действий.
2. Введение понятия семантика слова, жестовая символика, графическое обозначение.
3. Числовое оформление данного понятия: простые и составные именованные числа, преобразование именованных чисел (замена мелких мер крупными и наоборот); соотношение между единицами измерений одной метрической системы.
4. Действия с именованными числами (сложение, вычитание); действия с именованными и отвлеченными числами (умножение и деление).
Проводя первые уроки по теме «Именованные числа» я, к сожалению, убедилась в том, что большинство учащихся 5 класса не имеют реальных представлений о единицах измерения длины, с которыми они познакомились в начальной школе; не помнят и о соотношениях между этими мерами.
Поэтому, прежде чем переходить к действиям с именованными числами, я провела ряд занятий на повторение ранее изучаемого материала, опираясь на практический опыт своих учеников.
Метр.
С этой мерой длины школьники знакомятся в 3 классе, повторяют в четвертом и, по логике вещей, должны иметь четкие представления об этог' единице измерения. На практике выходит иная ситуация. Вот пример. Приношу на урок ленту, бичевку, веревку и предлагаю следующий вопрос:
- Как узнать длину ленты? (Надо измерить.)
-
Чем будем мерить? (Линейкой)
-
В каких единицах запишем ответ? (Молчание)
Вывод: у учащихся сформировано представление о необходимости выполнить измерительные действия. Однако большинство из них забыли как называются единицы измерения длины и как они записываются на письме. Понятие (слово) не подкреплено действием (жестом), символом.
Для активизации памяти предлагаю измерить длину класса:
- Чем будем мерить длину? (Линейкой)
- А есть ли другой инструмент? (Метр - большая деревянная линейка).
Словарная работа. МЕТР
В этот момент ставлю перед собой две задачи:
1. Подкрепить новое понятие практической деятельностью детей.
2. Довести до сознания учащихся, что метр - это определенное расстояние, протяженность.
- Ребята, у нас в классе только один деревянный метр, а вас 8 человек (т.е. создаю проблемную ситуацию). Что надо сделать, чтобы в работе принимали ученики всего класса?
Решить эту проблему предлагаю 2 способами: 1 способ. Раздаю всем детям заранее приготовленные полоски плотной бумаги длиной в 1м. Проводим с детьми измерение. По окончанию работы подводим итог: а) длину класса (и не только) можно измерить с помощью любого предмета, длина которого соответствует длине деревянного метра; б) этот способ не совершенен, т.к. предлагает использование предмета, который не всегда оказывается под рукой.
Таким образом, подвожу детей ко 2 способу. Предлагаю еще раз внимательно рассмотреть метр и сравнить его с собой. В результате этой работы, учащиеся сравнивают метр с расстоянием от плеча до кончиков пальцев вытянутой руки. Самостоятельно делают выводы: метр есть у каждого из нас, его можно показать на себе, этим метром можно производись измерительные действия. (Производим практические измерительные действия с веревкой, бичевкой, резинкой и др. предметами).
Систематизацию и закрепление полученных знаний провожу по таблице «Единицы измерения длины». (см. Приложение 7.)
Есть еще один момент в работе с единицами измерения на данном этапе: необходимо довести до сознания детей, что все меры, которые мы показываем на себе, являются приближенными, но это не ошибка, это жизненная необходимость.
Дециметр.
Понятие «дециметр» отрабатывается по аналогии с понятием «метр».
Создаю ситуацию «успеха»: предлагаю измерить ленту, бант, веревку. Длина этих предметов равна целому числу метров. Создаю проблемную ситуацию: предлагаю измерить парту. Ученики пользуются метром или меркой своего тела - получается остаток.
Делаем вывод: не все предметы можно измерить метром, есть другие единицы измерения длины, которые меньше метра, эти единицы помогут нам вычислить остаток. Ввожу понятие «дециметр». Еще раз измеряем парту, получаем результат: 1м 2дм.
Ставлю перед учащимися новую задачу: - Метр в классе один, вас -8 человек, каким способом можно измерить парты класса всем одновременно?
Такими вопросами подвожу детей к мысли о том, что необходимо эту меру длины найти на себе: рассматриваем деревянный метр, определяем количество делений, режем метровые бумажные ленты на 10 частей, сравниваем эти бумажные эквиваленты дециметра со своим телом, приходим к выводу: дециметр равен ширине ладони.
Словарная работа ДЕЦИМЕТР
Краткое обозначение на письме: дм Соотношение: 1м = 10дм
Закрепление по таблице «Единицы измерения длины» (см. Приложение 7)
Аналогично провожу работу над понятием «сантиметр» и «миллиметр». Перед тем как проводить урок по теме «километр», веду учащихся на экскурсию, где они реально увидят расстояние в 1км, пройдут это путь, сами. установят связь между расстоянием в 1км и временем, необходимым, чтобы пройти это расстояние. В дальнейшем, используя отработанную схему проведения уроков, учащиеся легко запоминают само понятие «километр», его обозначение на письме, графический символ, жест (см. Приложение 7)
Особое внимание на этом этапе работы уделяю заучиванию соотношений между единицами измерения длины: сколько в крупной мере мелких мер. Заучивание идет достаточно трудно. Для более легкого запоминания использую деятельностный прием «отстукивание» (отхлопывание). Приведу пример.
Игра «Молчанка»
Цель: изучение соотношения мер длины.
Содержание: «Вы немые. Вместо языка говорят ваши руки». Вопрос: Сколько в 1м - см?
Ответ:(100см) - ученики делают два стука по парте в соответствии с количеством нулей.
Вопрос: Сколько в 1км - м?
Ответ: (1000м) - три стука.
Вопрос: Сколько в 1дм - см?
Ответ: (10см) - один стук. И т. д.
Эту игру можно проводить и с использованием внешней речи, т.е. с проговариванием своих действий. В результате такой работы дети с 'интеллектуальной недостаточностью хорошо усваивают необходимые знания. После того, как все понятия уточнены, провожу работу по их закреплению. Для этой цели использую ряд приемов:
1. Физминутки (см. Приложение №6)
2. Сюжетно - ролевые игры, игры - пантомимы, игры - соревнования (см. Приложение № 5)
3. Слуховой, зрительный математический диктант.
4. Ввожу в устный счет занимательные задания типа: Что длиннее 1км или 1см?
Какая стена класса короче?
Как, без использования инструментов, измерить доску? И др.
5. Практические упражнения на уроке:
- выполнить измерение с использованием инструментов;
- выполнить измерения без использования инструментов (использовать мерки тела);
- определять расстояние (длину, размер) на глаз.
6. Письменные упражнения на доске, в тетради:
- начертить единицы измерения длины с помощью инструментов; без инструментов.
7.Задачи познавательного и занимательного содержания. (Приложение № 8).
*■'
Единицы измерения массы.
Перед проведением занятий по теме «Меры массы», веду учащихся на экскурсию в школьную столовую, где в подсобных помещениях расположены различных видов весы, разновесы. Школьники знакомятся с ними, включая в работу все анализаторы: слух, зрение, тактильные и мускульные ощущения.
В дальнейшем на занятиях повторяем меры «килограмм» и «центнер», и вводим новые понятия «грамм» и «тонна».
Работа по каждому понятию проводится отдельно. В основе учения каждого понятия лежит действие с предметами. Начинаю повторять меры массы с понятия «КИЛОГРАММ».
Ход урока.
1. Приношу ряд предметов: булка хлеба, пачка сахара, зерно пшеницы, гантели весом в 1кг, 5кг, весы.
2. Предлагаю, опираясь на чувственный опыт, ответить на вопрос: - Какие из предложенных здесь предметов весят один килограмм?
3. Предлагаю всем учащимся подержать на руке гирю массой 1кг, с тем, чтобы мускульно ощутить меру массы равную килограмму.
4. На одну руку кладу килограммовую гирю, на противоположную - пачку сахара. Предлагаю самостоятельно сделать выводы.
5. Возвращаюсь ко второму пункту, предлагаю отобрать предметы весом 1кг.
6. Словарная работа килограмм
7. Запись в тетради.
8. Практическая работа по отвешиванию и взвешиванию предметов, весом 1кг.
Грамм.
С этой единицей измерения массы знакомятся впервые. Создаю жизненную ситуацию, в которой бы ученики почувствовали необходимость в более мелкой единице массы.
- Сколько ложек сахара вы кладете в стакан чая? Какова масса этого сахара? Сколько нужно пакетиков, чтобы заварить один стакан чая? Какова масса этого пакетика?
Учащиеся затрудняются ответить, однако им становиться очевидно, что с помощью гири в 1кг нельзя определить массу сахара или пакетика чая, эта слишком большая мера.
Из жизненного опыта, из представлений, полученных на экскурсии, учащиеся припоминают, что есть другие гири, которые измеряют предметы массой меньше 1кг. Ввожу понятие ГРАММ
Предлагаю рассмотреть, ощутить гирю массой в 1 г. Закрепляю действие жестом, словом: легко или тяжело. Даю возможность сравнить: гиря массой 1кг и гиря массой в 1г. Дети делают соответствующие выводы.
Предлагаю определить массу предметов, лежащих на столе. Опыт показал: все предметы, которые меньше и легче одного килограмма, ученики приводят в пример, как предметы массой 1г. Чтобы исключить подобные ошибки, знакомлю учеников с другими разновесами: 5г, 10г, 20г, 50г, 100. 200г, 500г. На этом этапе провожу практическую работу по взвешиванию различных предметов.
Соотношение между килограммом и граммом ученики устанавливают сами: гирю в 1кг они уравновешивают на весах другими гирями и подсчитывают, сколько потребовалось граммов. Таким образом, они устанавливают соотношение: 1кг = 1000г
Центнер.
Чтобы вспомнить, что такое «центнер» предлагаю еще одну экскурсию к столовую. Измеряем массу мешков с картофелем на специальных весах. Выясняем, что масса одного мешка приблизительно равна 50 кг, предлагаю поднять мешок с картофелем, чтобы мускульно ощутить массу равную 50 кг Предлагаю ученикам решить задачу: «Масса одного мешка с картофелем равна 50кг. Чему равна масса двух таких же мешков с картофелем?». Деть правильно находят решение задачи, получают 100кг. Ставим на весы второй такой же мешок с картофелем, получаем 100кг. Вновь предлагаю поднять этот вес. Навалившись всем классом, они приподнимают эти мешки с картофелем, тем самым мускульно ощущают эту меру массы. Теперь я твердо убеждена, что мои ученики не спутают такие меры как килограмм, грамм и центнер. Уже на занятиях, ввожу понятие ЦЕНТНЕР, осуществляю словарную работу.
Выясняем, что 100кг это то же самое, что 1ц. Дети самостоятельно выводят соотношения мер: 1ц = 100кг. Предлагаю своим ученикам запомнить эту картинку и в дальнейшей работе пользуюсь ею.
Тонна.
Использовать практическую деятельность при изучении этой меры массы невозможно. При изучении понятия «тонна» использую метод припоминания, т.е. вызываю у детей конкретные образы предметов, масса которых превышает 1 центнер. Таким образом, я материализую понятие, делаю его конкретным, связывая с реальным предметом. Так например,, предлагаю рассмотреть картинку, где изображена машина на весах, масса которой 1000 кг.
Ученики самостоятельно приходят к выводу, что машина весит 1000 кг, а 1000 кг = 1т. Ввожу понятие ТОННА провожу словарную работу, предлагаю игровой материал для закрепления(см. Приложение №5) Соотношение мер «тонна- килограмм», «тонна- центнер» дети делают самостоятельно. Для закрепления темы «Соотношение мер массы» использую прием «отстукивания» (отхлопывания) по аналогии с мерами длины.
Преобразование чисел, полученных при измерении.
Это обязательный этап в работе с именованными числами, проводится каждый раз перед выполнением действий с ними. Этот вид работы предполагает, что учащиеся должны:
а) знать названия мер, умело ими оперировать;
б) знать соотношения между единицами одной метрической системы;
в) уметь производить два действия - умножение и деление — на 10, 100 и 1000 (с остатком и без него).
Приемы, используемые в работе по преобразованию именованных чисел
1. Постановка учебной цели.
Создаю на уроке жизненную проблемную ситуацию, при решении которой учащиеся должны убедиться в необходимости преобразования именованных чисел.
а) из крупных мер в мелкие (раздробление):
«У меня в руках полоска бумаги длиной 1дм. Я отрезаю 15см. Какой длины полоска осталась?»
б) из мелких мер в крупные (превращение):
«Я пошла в магазин за продуктами. Кассир дал мне сдачу 300к (показываю учащимся). Вы видите, это целый мешок денег. Он тяжелый, не помещается в кошелек. Что же мне нужно сделать?»
2. Организация учебных действий.
а) Предлагаю учащимся самостоятельно отрезать от полосы бумаги 15см. Задаю вопросы:
- Какой длины полоска была?
- Сколько отрезали?
- Какой длины полоска осталась?
В результате проведенной работы, учащиеся приходят к выводу: надо заменить 1м сантиметрами. Теперь можно ответить на поставленный вопрос.
3. Первичное закрепление с комментированием. Ввожу алгоритм действий (см. Приложение №4)/
а) Зная соотношение мер длины, учащиеся запоминают 1м = 100см. Устно выполняют вычисления и получают ответ:
- Осталась полоска длиной 85см.
Для письменной работы предлагаю другое упражнение: Зм = ...см (первичное закрепление проводит учитель, опираясь на алгоритм действия, используя прием «отстукивания»)
1. - Проверим есть ли пропущенные разряды.
В одном метре 100 сантиметров. Это два нуля. Постучите, (дети отстукиваю; количество нулей) Приписываем пропущенные разряды справа, получаем следующую запись: 3м 0 0см
2. - Заменим крупные меры мелкими.
Предлагаю учащимся закрыть ладонью (пальчиком) крупную меру и переписать оставшееся число и наименование без изменений: 3м 0 0см= 300см.
Вывод: Крупную меру заменили мелкой.
При выполнении письменных действий использую последний пункт алгоритма действий и метод «волна».
3. - Заменим мелкую меру крупной.
а) В одном метре сто сантиметров. «Чтобы разделить число на 100, надо отбросить справа два нуля»: 3ØØ см
б) - Чтобы в тетрадях не было зачеркиваний, я буду использовать «волну»: обведу волнистой линией столько цифр, сколько надо отбросить: 300см
в) - Все, что стрит впереди «волны» - это крупная мера, остальные цифры
- мелкие меры: 3м 0 0см
4. Самостоятельная работа.
А) по вариантам использование алгоритма
Б) в парах действий
5. Проведение тренировочных упражнений.
Сильные учащиеся выполняют задание по учебнику самостоятельно. Учащиеся, которые занимаются по программе со сниженным уровнем требований - работают у доски, под контролем учителя.
Вся работа по преобразованию именованных чисел строится с учетом постепенного усложнения материала: от более легких случаев — к более сложным:
Действия с именованными числами.
Действия над числами, полученными от измерения величин. Выполняются так же, как действия над многозначными числами, с той лишь разницей, что при числах должны быть записаны наименования единиц измерения.
Действия над числами, полученными от измерения величин, опираются не знания учащимися единиц измерения и их соотношение, а также умение выразить одни меры другими.
Обучая учащихся выполнять действия сложения, вычитания, умножения и деления, придерживаюсь следующих правил:
1. Каждое действие объясняю, включив всех учащихся в предметно- практическую деятельность и создав жизненную необходимую ситуацию.
2. Вся работа строится в соответствии с алгоритмом действий (см. Приложение №4)
3. У именованного числа должно быть два наименования: впереди - крупная мера, затем мелкая. Если дано одно наименование, дополняю его вторым, в зависимости от соотношения мер.
4. Работа строится с учетом постепенного усложнения материала: от простых случаев к сложным.
5. Результативность опыта.
Таким образом, в данном опыте получен следующий результат.
Изучая метрическую систему мер, действия с именованными числами, их преобразование, учебный процесс строился на активной познавательной деятельности учащихся, которые получали новые знания не в готовом виде, а «открывали» их сами в процессе выполнения действий с предметами под контролем учителя. В конце каждой четверти, в 5-а классе проводила контрольный срез по данной теме (см. Приложение № 1), я убедилась, что уч-ся получили прочные знания о мерах длины и массы. Можно отметить повышение активности, появился интерес к предмету. В ходе урока принимали участие как сильные, так и слабые учащиеся.
Такие приемы запоминания ед. измерения как жестовый, а соотношение единиц измерения, как простукивание хорош еще и тем, что дает возможность активизировать все анализаторы, а значит повысить качество усвоения и запоминания нового материала. А так же позволяет легко припомнить полученные знания в нужный момент, стоит показать и они «всплывают» в памяти, в сознании ребенка.
Вывод: Предложенная система работы над числами, полученными при измерении эффективна при обучении учащихся с интеллектуальной недостаточностью.
III. Перспективы использования опыта в массовой педагогической практике.
1. Условия функционирования опыта.
Опыт функционирует в ГОУ «Котовская специальная /коррекционная/ общеобразовательная школа- интернат VIII вида».
Продолжительность уроков в данной школе – 40 минут, самоподготовки нет. Во второй половине дня ребята посещают факультативные занятия, кружки, секции. Уроки проводятся в кабинете математики для 5-9 классов со стандартным набором инвентаря и приспособлений. В классе имеется необходимый материал для уроков математики, опорные таблицы, алгоритмы, схемы к задачам, опросники по всем темам, дидактический материал, измерительные инструменты, макеты геометрических фигур, дополнительная литература по предмету. Занятия по предмету проходят в одну смену. Учащиеся обучаются по программе специальных (коррекционных) образовательных учреждений VIII вида.
В 5-а классе 8 учащихся: 4 мальчика и 4 девочки. Класс по знаниям «средний»: 4 ученика занимаются по основной программе 5-го класса хорошо, 3 ученика - удовлетворительно, один ученик занимается по программе с заниженными требованиями по основным предметам.
По особенностям познавательной деятельности, работоспособности, состояния внимания и поведения состав учащихся разделен на группы:
-
Дети с неосложненной формой олигофрении:
Дмитрий К.,
Кристина Ш.
Екатерина Р.
Александр К.
Елизавета Б.
-
Дети-с отклонениями в здоровье, характеризующиеся неустойчивостью эмоционально- волевой сферы с преобладанием процесса торможения:
Татьяна Б.
Артем П.
Классный коллектив находится на стадии формирования. Взаимоотношения между ребятами доброжелательные. Основная группа ребят хорошо поддается педагогическому влиянию. Все ребята посещают факультативные занятия по математике, которые проходят один раз в неделю (2 часа), а так же посещают кружки и секции.
Автор опыта имеет высшее образование, по специальности олигофренопедагогика. В данной школе работает 9 лет. На протяжении своей педагогической деятельности принимала активное участие в районных МО, областных семинарах на базе своего учреждения, в педагогических и методических советах школы, является руководителем МО учителей естественно- математического цикла шестой год, активно занимается самообразованием.
2. Теоретико- практические основы опыта.
Данный опыт опирается на традиционную методику обучения математике, представленную В.В. Эк и М.Н. Перовой, на исследования Л.С. Выготского в области психологии и собственные авторские разработки приемов и средств обучения.
3. Перспективы и возможности использования опыта в массовой общеобразовательной практике.
Данный опыт может быть полезен учителям математики и начальных классов специальных (коррекционных) школ VIII вида и средних общеобразовательных школ.
Рекомендации будущим пользователям опыта.
Последователям опыта рекомендую учесть следующее:
-
Чтобы научить детей с интеллектуальной недостаточностью метрической системе мер; преобразованию именованных чисел и действий с ними, надо создать жизненную ситуацию и включить всех учащихся класса в предметно- практическую деятельность, в результате чего учащиеся увидят необходимость изучения данного материала;
-
Работая над новым материалом, следовать по строго установленным этапам действий. Работу вести систематически из урока в урок, из класса в класс. Желательно начинать с начальных классов.
-
Закрепление знаний по данной теме и умений производить на уроках математики, на других учебных предметах, особенно на уроках трудового обучения, при работе на пришкольном участке. Успех здесь зависит от целенаправленной работы всех учителей и воспитателей, работающих с коллективом учащихся.
ЛИТЕРАТУРА.
-
Л.С. Выготский, «Основы дефектологии» т.4,т.5 Москва «Педагогика», 1984.
-
М.Н. Перова, Методика преподавания математики во вспомогательной школе. Москва, «Просвещение», 1989.
-
М.Н. Перова, Дидактические игры и упражнения во вспомогательной школе. Москва, «Просвещение», 1975.
-
В.В. Эк, Обучение математике учащихся младших классов вспомогательной школы. Москва, «Просвещение», 1990.
-
Программы для 5-9 классов специальных (коррекционных) общеобразовательных учреждений VIII вида: СБ.1.-М.: Гуманит. Изд. Центр, ВЛАДОС, 200.
-
М. Волович «Как успешно обучать математике». Приложение к газете «Первое сентября», «Математика» №3,6,8,10, 12 за 1997 г.
-
Обучение детей с нарушениями интеллектуального развития: (Олигофренопедагогика): Учеб. Пособие для студ. Высш. Пед. Учеб. Заведений / под ред. Б.П.Пузанова. - М.: Издательский центр «Академия», 2003.
![]()
ПРИЛОЖЕНИЕ № 1
МОНИТОРИНГ УРОВНЯ
СФОРМИРОВАННОСТИ ЗНАНИЙ И
УМЕНИЙ ПО ТЕМЕ
«МЕТРИЧЕСКАЯ СИСТЕМА МЕР»
УЧАЩИХСЯ 5 «А» КЛАССА.
ЦЕЛЬ: Проследить и сравнить динамику усвоения знаний и умений по теме «Метрическая система мер» у учащихся 5 «А» класса с интеллектуальной недостаточностью, обучающихся по системе основанной на активном участии ребят в процессе овладения новыми знаниями
ЗАДАЧИ: 1 .Проследить динамику усвоения знаний и умений по теме «Метрическая система мер» за год.
2.Проанализировать полученные результаты. 3 .Дать оценку эффективности представленной системы работы над темой «Метрическая система мер».
ОБЪЕКТ ИССЛЕДОВАНИЯ: Учебно-воспитательный процесс в 5 «А» классе за 2007-2008 учебный год.
ПРЕДМЕТ ИССЛЕДОВАНИЯ: Условия и факторы препятствующие и стимулирующие формирование знаний о единицах измерения , о их соотношениях , и умений преобразовывать именованные числа и выполнять действия с ними.
ДИНАМИКА УСПЕВАЕМОСТИ ПО ТЕМЕ «МЕТРИЧЕСКАЯ СИСТЕМА МЕР» В 5 «А» КЛАССЕ.
|
№ п.п. |
Ф. И. |
1 четверть |
2 четверть |
3 четверть |
4 четверть |
|
1 |
Борисова Т. |
2 |
2 |
3 |
3 |
|
2 |
Брух Л. |
2 |
3 |
3 |
4 |
|
3 |
Клыков Д. |
3 |
4 |
5 |
5 |
|
4 |
Курин с. |
2 |
3 |
3 |
4 |
|
5 |
Литвинов и. |
3 |
4 |
4 |
5 |
|
6 |
Подин А. |
2 |
2 |
3 |
3 |
|
7 |
Рудомётова К. |
3 |
4 |
4 |
5 |
|
8 |
Швец К. |
3 |
4 |
5 |
5 |
(Контрольные срезы по теме за 1, 2, 3, 4 четверти.)
|
Оценка |
1 четверть |
2 четверть |
3 четверть |
4 четверть |
|
«5» |
— |
— |
2 |
4 |
|
«4» |
— |
4 |
2 |
2 |
|
«3» |
4 |
2 |
4 |
2 |
|
«2» |
4 |
2 |
— |
— |
|
«1» |
— |
— |
— |
— |
1чет
3четв.
ГИСТОГРАММА УЧЁТА УСПЕВАЕМОСТИ
ПО ЧЕТВЕРТЯМ
Анализ мониторинга уровня сформированности знаний и умений по теме «Метрическая система мер» у учащихся 5 «А» класса . Мониторинг проводился в течение всего 5 класса. Из таблицы и гистограммы, представленных в мониторинге, видно , что описанная система работы над числами ,полученными при измерении, позволяет всем ребятам повысить уровень успеваемости и добиться положительных результатов. Шесть учащихся усвоили тему «Метрическая система мер» хорошо и отлично. Двое - удовлетворительно, но это связанно с особенностями их психических процессов.
ВЫВОДЫ: Повышению уровня сформированности знаний и умений по теме «Метрическая система мер» способствуют : 1 .Активной познавательной деятельности учащихся , которые получают новые знания не в готовом виде , а «открывают» их сами , в процессе выполнения действий с предметами под контролем учителя. 2.Повышение уровня мотивации учебной деятельности ,через :создание жизненных ситуаций , определение значимости изучаемого материала , личный опыт учащихся.
3.Приемы запоминания , которые активизировали бы как можно больше анализаторов.
ПРОБЛЕМЫ: 1 .Обучение, некоторых детей, по данной теме, затруднено в силу их диагноза. 2.На изучение темы «Метрическая система мер» по программе отводится недостаточное количество часов.
3.Рассматриваемая тема является одной из самых трудных для учащихся с интеллектуальной недостаточностью.
ОБЩИЕ ВЫВОДЫ :
l.Bce поставленные задачи были выполнены. Данный мониторинг показывает эффективность применения описанной системы работы над числами , полученными при измерении.
2.Наряду с положительными результатами есть и недостатки : двое учащихся (Таня Б. и Артем П.) по итогам за год имеют низкий уровень знаний по теме. Причина: учащиеся занимаются по программе с заниженными требованиями. З.В целом работа ведется в правильном направлении.
РЕКОМЕНДАЦИИ НА 2008-2009 УЧЕБНЫЙ ГОД. 1 .Продолжить работу по данной системе работы с этими же учащимися в 6 классе.
2.Продолжить мониторинговую деятельность по данному направлению. 3.Преемственность в работе по данной теме с учителями начальных классов и трудового обучения.
ПРИЛОЖЕНИЕ № 2.
АЛГОРИТМЫ, ИСПОЛЬЗУЕМЫЕ В РАБОТЕ С ИМЕНОВАННЫМИ ЧИСЛАМИ,
АЛГОРИТМЫ.
1. Выражение в более крупных единицах измерения .
1.Определить крупную единицу
измерения.
2.Вспомнить: , ,
3.Отделить мелкие единицы. 4,Оставшиеся - крупные единицы.
2. Выражение в более мелких единицах измерения .
1.Вспомнить: .,..,...
2.Проверить, есть ли пропущенный разряд. 3.Закрыть наименование крупных единиц. 4.Выразить в мелких (оставшихся) единицах.
3. Действия с именованными числами.
1 .Проверить, есть ли пропущенный разряд
2.3аменить крупные единицы мелкими.
3.Выполнить действие в столбик.
4.3аменить мелкие единицы крупными
- Международный вебинар «Лицевая гимнастика: комплексы упражнений, подготовка и методика проведения»
- Вебинар «Игры-эксперименты с дошкольниками: воспитываем потребность в познавательном общении со взрослыми, стремление наблюдать, сравнивать, исследовать, устанавливать причинно-следственные связи (ФОП ДО)»
- Вебинар «Краеведческая работа библиотек как средство интеграции в социокультурное пространство региона: традиционные формы, новые технологии»
- Международный вебинар «Цифровые образовательные ресурсы, дистанционные образовательные технологии, электронное обучение в работе с обучающимися с нарушениями зрения»
- Международный вебинар «Создание безопасной образовательной среды в образовательной организации в рамках реализации федерального проекта “Цифровая образовательная среда”»
- Международный вебинар «Приоритетные ориентиры в системе “государство – отдых – ребёнок”, принципиальные подходы к сфере отдыха и оздоровления детей, современные формы, методы и технологии организации отдыха и оздоровления детей»





