Муниципальное бюджетное учреждение

средняя общеобразовательная школа №10

муниципального образования

г. Новороссийск

УРОК МАТЕМАТИКИ В 5 КЛАССЕ

ПО ТЕМЕ:

«ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД»

ИЗ ГЛАВЫ

«ГЕОМЕТРИЧЕСКИЕ ТЕЛА»

УМК ЗУБАРЕВА И.И., МОРДКОВИЧ А.Г.

Волкова Ольга Алексеевна

учитель математики

МБОУ СОШ №10

г. Новороссийск

Урок 2.

Тема урока: «Прямоугольный параллелепипед»

Цели урока:

а) обучающая - познакомить учащихся с элементами прямоугольного

параллелепипеда;

- ввести понятие развертки прямоугольного

параллелепипеда;

- вывести формулу площади поверхности

прямоугольного параллелепипеда;

- вывести формулу суммы длин всех ребер

Прямоугольного параллелепипеда;

б) развивающая - познакомиться с новыми понятиями, связанными с

прямоугольным параллелепипедом;

- развитие пространственного воображения;

- научиться сравнивать геометрические тела;

в) воспитывающая - привитие навыка аккуратности при построении

чертежа;

- анализировать увиденное и делать логические выводы.

Задачи урока: - закрепить навыки построения чертежа пространственной

фигуры;

- научиться применять формулу площади поверхности

прямоугольного параллелепипеда и формулу суммы

длин всех его ребер.

Оснащение урока:

компьютер и проектор для демонстрации презентаций; на каждом ученическом столе цветной пластмассовый кубик и бумажная

модель прямоугольного параллелепипеда; набор различных моделей куба и прямоугольного параллелепипеда у учителя.

Ход урока.

1. Организация начала урока.

Здравствуйте! Сегодня на уроке мы продолжим путешествие по стране Геометрия. Оказывается, в этой стране у нашего куба живут родственники, с которыми мы сегодня познакомимся.

2. Сообщение темы, цели и задач урока.

Родственники обычно похожи друг на друга, поэтому мы сегодня познакомимся с родным братом нашего куба, а зовут его (слайд № 1)

Прямоугольный параллелепипед. На уроке нам будет опять помогать компьютер, сейчас он объявил нам тему сегодняшнего урока, запишите её в тетрадь.

3. Актуализация знаний учащихся.

У этой геометрической фигуры длинное и трудное название, возможно, не все из вас слышали это название. А встречаются ли в жизни предметы такой формы? Назовите их.

[Коробки, ящики, книги, комнаты]

4. Усвоение новых знаний.

Компьютер подсказывает, чем мы сейчас будем заниматься

( слайд № 2).

Запишите это в тетрадь. А пока будете писать подумайте, что одинаковое вы заметили у родных братьев – у куба и прямоугольного параллелепипеда. Записали? Теперь сравните модели куба и прямоугольного параллелепипеда, которые у вас на парте и на экране. Что у них одинаковое? (слайд №3)

Какие элементы куба повторяются у прямоугольного параллелепипеда?

[ Грани, вершины, ребра]

Является ли прямоугольный параллелепипед многогранником?

[ Да]

Сравните количество граней, вершин, ребер.

Все одинаковое?

А теперь давайте найдем различие у этих двух фигур. Рассмотрите грани куба и прямоугольного параллелепипеда. Есть ли у них отличие, какая фигура является гранью куба, а какая гранью параллелепипеда?

[ У куба – квадрат, у прямоугольного параллелепипеда - прямоугольник]

Продолжаем сравнивать дальше. Что вы можете сказать за грани куба?

[ Все грани - квадраты равны]

Есть ли равные грани у прямоугольного параллелепипеда?

Как они располагаются?

[ Напротив друг друга]

Поэтому равные грани называются противоположными. Посмотрите на экран и на модели и назовите равные противоположные грани прямоугольного параллелепипеда – это дно и крышка, боковые грани, передняя и задняя грани.

Посмотрите, на экране новая запись, ( слайд № 4),

компьютер просит нас изобразить прямоугольный параллелепипед. Обратите внимание на эти каркасные модели прямоугольного параллелепипеда и куба, которые стоят на столе. Можете ли вы различить, какая из фигур, прямоугольник или квадрат, является донышком? Нет, не можете, поэтому донышко прямоугольного параллелепипеда мы изобразим точно так же как и донышко куба.

Компьютер будет подсказывать нам, что нужно делать (слайд № 5)

( Как и при построении чертежа куба начало работы ведется параллельно на доске и на экране, при построении вертикальных ребер откладывают больше клеточек, чем первоначальный отрезок).

Мы выяснили, что гранью прямоугольного параллелепипеда является прямоугольник. Как называем стороны прямоугольника?

[ Длина и ширина]

Подпишем у сторон донышка, где длина и ширина ( слайд № 5), но боковые грани то же прямоугольники и вертикальные ребра этих прямоугольников называют высота (слайд № 5)

Теперь возьмите красный карандаш и выделите все вертикальные ребра.

Что вы можете сказать о длине этих ребер? Сколько их? Проверьте свои выводы на модели.

Есть ли еще у прямоугольного параллелепипеда равные ребра? Назовите их.

Правильно, это длина. Сколько таких ребер? Выделите их синим цветом, а ширину выделим зеленым цветом ( слайд № 5) Сколько ребер каждого цвета? Проверяйте себя по модели.

[ Одинаковых ребер по 4]

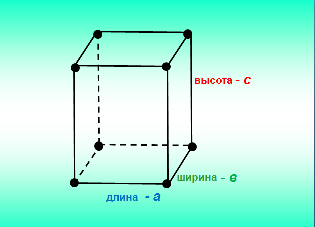
Длина, ширина и высота прямоугольного параллелепипеда называются измерениями прямоугольного параллелепипеда. Но слова длина, ширина и высота долго говорить и писать, поэтому длину обозначают буквой a, длину буквой b, а высоту буквой с (слайд № 5)

Компьютер просит нас записать что-то в тетрадь ( слайд № 6 и слайд №7)

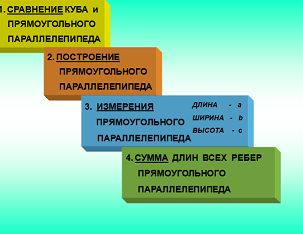
Ребята, мне хочется сделать новую каркасную модель прямоугольного параллелепипеда. Давайте подумаем, как рассчитать, сколько проволоки мне понадобится?

Если длина прямоугольного параллелепипеда a, то сколько нужно проволоки на все ребра длиной в a ?

[ 4a]

А на все ребра ширины, если ширина прямоугольного параллелепипеда b?

А на все ребра высоты c ?

[ 4b ; 4c]

А сколько всего?

Считаем, сколько понадобится проволоки, что нужно для это сделать?

Посмотрим, как предлагает нам компьютер это записать ( слайд № 8)

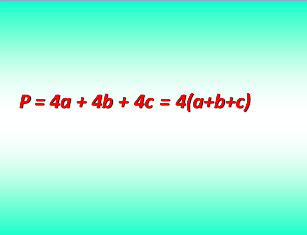
5. Первичное закрепление знаний.

Посмотрите, компьютер предлагает нам задачу (слайд № 9).

Решим ее на доске, а потом сверимся с компьютером. ( Запись условия приготовлена заранее на откидном крыле доски. Проверка решения -слайд №9 )

6.Усвоение новых знаний.

Компьютер опять предлагает нам сделать запись в тетрадь

( слайд № 10),

выполним его просьбу: развернем наш прямоугольный параллелепипед (слайд № 11 и слайд№12).

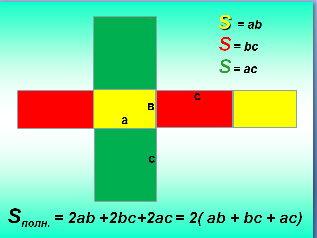
Из каких фигур состоит развертка?

[ Два желтых прямоугольника, два красных, два зеленых]

Как найти площадь желтой грани?

Как найти площадь красной грани?

Как найти площадь зеленой грани?

Что нужно сделать, чтобы найти площадь всей поверхности прямоугольного параллелепипеда?

[ Умножить каждую площадь на два и полученные результаты сложить]

Так ли это? Спросим у компьютера, и сделаем в тетрадь запись формулы полной поверхности прямоугольного параллелепипеда (слайд № 12)

6. Первичное закрепление знаний.

Компьютер опять просит нас решить задачу (слайд № 13), решим ее на доске и проверим себя.

7. Обобщение и систематизация.

Решим на доске задачу:

a = 8

b =4

c = 10

Найти 1) сумму длин всех ребер

2) площадь поверхности параллелепипеда

Сверим свое решение ( слайд № 14)

А может ли гранью параллелепипеда служить квадрат?

Если может, то где эта грань?

Ответ вам подскажут эти модели из набора.

8. Подведение итогов урока.

С какой новой фигурой мы сегодня познакомились?

Где встречается в жизни прямоугольный параллелепипед?

Какая фигура является гранью параллелепипеда?

Может ли квадрат быть гранью параллелепипеда?

По сколько равных граней параллелепипеда?

По сколько равных ребер?

9. Домашнее задание: изготовить развертку параллелепипеда с измерениями a =3 см, b=4см, c=5см и изготовить из неё модель прямоугольного параллелепипеда.

Пояснительная записка

Данная разработка изучения темы «Геометрические тела» в 5 классе, УМК И.И. Зубарева, А.Г. Мордкович, содержит три интерактивных урока. Каждый урок – это презентация, выполненная в Power Point

Интерактивный урок №1 «Куб» в изучении темы «Геометрические тела». На уроке рассматриваются свойства куба, алгоритм построения его чертежа, формула площади поверхности куба.

Интерактивный урок №2 «Прямоугольный параллелепипед» в изучении темы «Геометрические тела». На уроке рассматриваются свойства прямоугольного параллелепипеда, схожесть и различие между прямоугольным параллелепипедом и кубом, алгоритм построения его чертежа, формула поверхности прямоугольного параллелепипеда и суммы длин его ребер.

Интерактивный урок №3 в изучении темы «Геометрические тела». На уроке рассматриваются единицы измерения длины, площади и объема, формула вычисления объема куба и прямоугольного параллелепипеда

Данная разработка может использоваться как в начальной школе при знакомстве с геометрическими телами так и в старших классах при повторении свойств геометрических тел

Муниципальное бюджетное учреждение

средняя общеобразовательная школа №10

муниципального образования

г. Новороссийск

УРОК МАТЕМАТИКИ В 5 КЛАССЕ

ПО ТЕМЕ: «КУБ»

ИЗ ГЛАВЫ

«ГЕОМЕТРИЧЕСКИЕ ТЕЛА»

УМК ЗУБАРЕВА И.И., МОРДКОВИЧ А.Г.

Волкова Ольга Алексеевна

Учитель математики

МБОУ СОШ №10

г. Новороссийск

Урок 1

Тема урока: «Куб»

Цели урока:

а) обучающая - познакомить учащихся с элементами

- ввести понятие развертки куба, модели тела;

- вывести формулу площади поверхности куба;

б) развивающая - развивать математическое мышление;

- развитие пространственного воображения;

- научиться переводить наглядную картинку – чертеж в логический вывод, в формулу;

в) воспитывающая - воспитание аккуратности при построении чертежа;

- воспитание четкости мысли при построении логических выводов.

Задачи урока: - сформировать навыки построения чертежа пространственной фигуры;

- научиться применять формулу площади поверхности куба.

Оснащение урока: компьютер и проектор для демонстрации презентаций; на каждом ученическом столе по два цветных пластмассовых кубика и набор разверток; набор различных моделей куба у учителя.

Ход урока

1.Организация начала урока.

Здравствуйте! Сегодня мы отправимся в путешествие в одну очень интересную страну знаний, в страну под названием Геометрия. Живут в этой стране геометрические фигуры или геометрические тела. Все об этой стране вы узнаете в старших классах, а сегодня она поведает нам лишь некоторые свои тайны.

2.Сообщение темы, цели и задач урока

Посмотрите на рисунок (слайд №2),

на котором изображены две группы геометрических тел. Как вы думаете, по какому признаку эти геометрические тела разбиты на две группы? [ Одни тела круглые, а другие состоят из плоских фигур]

Сегодня мы будем изучать хорошо вам известное геометрическое тело, оно стоит у каждого на столе, и я держу его в руках. Что это за геометрическое тело? К какой группе тел оно относится? Правильно ли мы назвали это геометрическое тело подскажет компьютер, он объявит нам тему нашего урока, а мы запишем ее (слайд №3) в тетрадь.

Мы угадали правильно, сегодня мы будем говорить о кубе. Узнаем, как называются элементы куба, научимся чертить куб, узнаем, как находить площадь поверхности куба , где в жизни мы встречаемся с кубом. Руководить нашей работой будет компьютер, он будет подсказывать нам, что нам нужно делать.

3. Актуализация знаний учащихся.

Скажите, ребята, вы раньше встречались с кубом? Правильно, все мы в детстве играли в кубики. А все ли вы знаете о кубе? Давайте себя проверим.

3. Изучение нового материала.

Посмотрите на компьютер, на экране появилась новая запись (слайд №4),

запишем ее в тетрадь. Компьютер просит, чтобы мы внимательно посмотрели на куб.

Давайте возьмем в руки куб и рассмотрим его.

- Из чего состоит поверхность куба?

[ Из квадратиков]

- А что мы знаем о сторонах квадрата?

Посмотрите, у каждых соседних квадратиков одна сторона общая, что тогда мы можем сказать о всех квадратиках, из которых состоит куб?

[ Все квадраты равны]

Каждый такой квадратик называется гранью. Посчитайте, сколько таких граней-квадратиков у куба? Правильно, 6 граней, т.е. их много, поэтому куб еще называют многогранником.

У каждой грани есть граница. Проведите пальцем по границе каждого квадратика. Каждая граница называется ребро. Сколько ребер у куба?

[ 12 ребер]

Ребра квадратиков сходятся вместе и образуют углы куба. Каждый такой угол куба называется вершина. Из каждой вершины выходят ребра. Сколько ребер выходит из каждой вершины?

[ 3 ребра]

3. Первичное закрепление знаний

Давайте повторим:

Сколько граней у куба?

Сколько вершин у куба?

Сколько ребер у куба?

Сколько ребер выходит из одной вершины?

Сколько ребер у каждой грани?

Сколько соседних граней имеет каждая грань?

3. Усвоение новых знаний

Посмотрите, на экране появилась новая запись (слайд №5), давайте перенесем ее в тетрадь и будем учиться рисовать куб. Компьютер будет подсказывать, как это делать.

(Построение идет на доске с параллельным показом

слайда №6.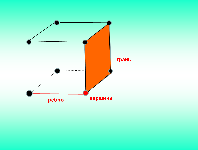

Для быстроты построения лучше взять за длину ребра четное количество клеточек).

Мы построили куб, подпишите его элементы. Вы обратили внимание, что некоторые ребра я изобразила сплошной линией, а некоторые – пунктирной? Как вы думаете, почему это, в чем различие? Сколько граней у куба мы всегда видим?

Мы с вами устали, давайте отдохнем и разгадаем ребусы(слайд №7 и №8).

Нам удалось расшифровать два слова: развертка и модель. Со словом модель мы встречались много раз, а вот как оно связано с кубом? Как вы думаете? Правильно, кубов много, они бывают разных размеров, изготовлены из разных материалов, но наш каждый куб является представителем всего семейства, поэтому наш куб – модель.

А вот слово «развертка» нам встретилось первый раз. На какое слово оно похоже? Посмотрите, компьютер советует, записать новое слово в тетрадь (слайд № 9)

Вот давайте развернем наш куб и посмотрим, что получится (слайд №10 и №11).

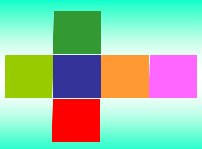
Во что развернулся куб? [ В 6 соединенных квадратиков]

А теперь подумайте над следующим вопросом: из любой развертки можно сложить куб? Посмотрите, на экране 8 разверток, из любой можно сложить куб?

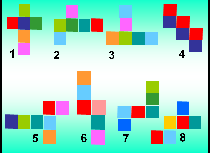
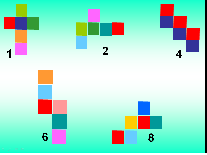
(Задача №922.Математика -5, Зубарева И.И., Мордкович А.Г. на экране, (слайд №12 и слайд №13), не могут быть разверткой куба №3, №5 и №7. Сразу отсевается №5, в ней 7 квадратов. Все остальные развертки вырезаны и на каждой парте лежит полный комплект, развертки находят перегибая выкройки и складывая куб.)

Выберите на развертках, где будет верхняя и нижняя грани. Подпишите на развертках буквы В и Н. У всех получилось одинаково? Почему получились разные отметки?

3. Применение новых знаний.

Мы с вами определили, что куб состоит из 6 квадратов. Как найти площадь квадрата? А шести квадратов? Посмотрите, компьютер показывает, какую запись мы должны сделать в тетрадь (слайд № 14).

Мы записали формулу площади поверхности куба.

А какая площадь поверхности у куба со стороной в 25 см? Проверим себя (слайд №15)

Знаете ребята, я так хочу поставить в нашем кассе аквариум в форме куба со стороной 1 м. Сколько стекла нужно будет купить?

[ 5 м²]

Почему 5м² , а не 6м² ? Правильно, рыбкам нужен воздух, какой грани у нас не будет?(слайд №16)

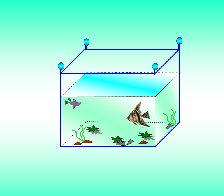
Где еще мы можем встретить куб?

[ Различные коробки, музыкальные центры, игрушки, украшения на люстрах]

3. Подведение итогов урока.

С какой геометрической фигурой мы сегодня работали?

С какими элементами куба мы познакомились?

Каких элементов 12? Каких 8? Каких 6?

Почему куб называют многогранником?

Какие новые слова мы узнали из ребусов?

Как найти площадь поверхности куба?

Где мы в жизни встречаемся с кубом?

3. Домашнее задание

На альбомном листе приготовить развертку куба со стороной 5см, изготовить из неё куб.

Найти площадь поверхности куба со стороной 12см.

Волкова Ольга Алексеевна

Учитель математики

Муниципальное бюджетное учреждение

средняя общеобразовательная школа №10

муниципального образования

г. Новороссийск

УРОК МАТЕМАТИКИ В 5 КЛАССЕ

ПО ТЕМЕ: «ОБЪЕМ»

ИЗ ГЛАВЫ

«ГЕОМЕТРИЧЕСКИЕ ТЕЛА»

УМК ЗУБАРЕВА И.И., МОРДКОВИЧ А.Г.

Волкова Ольга Алексеевна

Учитель математики

МБОУ СОШ №10

г. Новороссийск

Урок 3.

Тема урока: «Объем»

Цели урока:

а) обучающая - ввести понятия объёма тела;

- ввести понятие о единице измерения объема;

- вывести формулу объёма куба и прямоугольного

параллелепипеда;

б) развивающая - познакомиться с новыми понятиями;

- развитие познавательной активности с помощью

исторического материала;

- развитие элементов творческой деятельности

учащихся;

в) воспитывающая - воспитание точности корректности, логичности в

мышлении;

- воспитание прилежания, интереса к предмету.

Задачи урока: - научиться применять формулу объёма куба и прямоугольного параллелепипеда.

Оснащение урока: компьютер и проектор для демонстрации презентаций; на каждом ученическом столе набор маленьких цветных пластмассовых кубиков; набор различных моделей куба и прямоугольного параллелепипеда у учителя.

Ход урока

1. Организация начала урока.

Здравствуйте! Сегодня мы продолжим наше путешествие по стране Геометрия и рассмотрим еще одно важное свойство куба и прямоугольного параллелепипеда. Помогать нам в изучении нового свойства будет верный друг компьютер.

2. Сообщение темы, цели и задач урока.

Итак, тема сегодняшнего урока (слайд № 1),

запишите ее в тетрадь. Сегодня на уроке мы узнаем, что такое объем и как измеряется объем знакомых нам тел – куба и прямоугольного параллелепипеда.

3. Актуализация знаний учащихся.

Что такое объем? Кто знает? Я думаю, вы уже слышали это слово. Как рассказать, что такое объем вот этой банки? ( Банка стоит на столе)

Объем – это количество воды, песка, воздуха, крупы, которое войдет в эту банку.

4. Усвоение новых знаний.

Как же измеряется объем?

Для начала вспомним, как измеряются длины отрезков.

Правильно, единицей измерения длины – сантиметром. Вспомните, что мы с вами говорили на уроках об эталонах. Молодцы, вспомнили.

Компьютер просит сделать запись тетрадь (слайд №2)

Нарисуем в тетради отрезок длиной в 1 см (параллельно учитель ведет запись на доске)

А как измеряется площадь?

Правильно, единицей измерения площади – квадратным сантиметром.

Сделаем запись в тетрадь (слайд №3)

и изобразим квадратный сантиметр.

Значит, прежде чем что-то измерить, необходимо выбрать единицу измерения

А объем измеряется единицей измерения объема, делаем запись в тетрадь ( слайд № 4),

и посмотрите на единицу измерения объема - это кубик с ребром в один сантиметр. Вот он, посмотрите на него (модель): он такой маленький, а может измерить объем любого тела. Сколько кубиков войдет в тело, такой и объем тела. Кто еще знает, какие существуют единицы измерения объема? Правильно, баррель. А что это такое? Это бочка емкостью 159 литров. А Древнем Риме единицей измерения объема была амфора 25,5 литра

Нарисуем единицу измерения объёма в тетрадь, куб мы уже научились рисовать.

Давайте попробуем определить объем тел, сложенных из таких кубиков (слайд № 5),

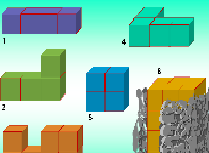
чтобы вам было проще, сложите такие тела из кубиков у вас на столе.

А теперь попробуем определить объем куба. Возьмем куб со стороной 5 см (слайд № 6) и разрежем его на такие маленькие кубики со стороной в 1 см.

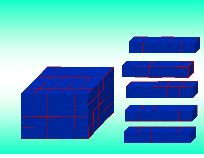
Посмотрите, что получилось. Сколь же этих маленьких кубиков, попробуем посчитать. На сколько слоев разрезали куб? Сколько кубиков в каждом слое? Сколько кубиков в 5 слоях?

Мы получили, что объем куба со стороной 5 см равен ( слайд № 7) и получили формулу для вычисления объема куба.

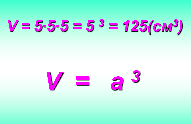
Проделаем то же с прямоугольным параллелепипедом с измерениями a =3 см, b=4см,

c=5см и разрежем его на кубики со стороной в 1 см (слайд №8).

На сколько слоев разрезали параллелепипед? Сколько кубиков в каждом слое? Сколько кубиков в 5 слоях? Мы получили, что объем равен (слайд № 9)

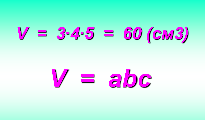
и формулу для вычисления объема параллелепипеда.

5. Первичное закрепление знаний.

1. Найти объем куба со стороной 6 см. (Приготовленная запись условия на откидном крыле)

a = 6 см V = a³ = 6 ³ = 216 ( см³)

Найти V

2. Найти объем параллелепипеда с измерениями a =5 см, b=6 см, c=7 см

a =5 см V = abc = 5∙6∙7 = 210 ( см³ )

b=6 см

c=7 см

Найти V

6. Обобщение и систематизация.

1. № 940.Математика – 5.Зубарева И.И., Мордкович А.Г. Приведите контрпример для утверждения: любые два прямоугольных параллелепипеда, имеющие равные площади поверхности, имеют равные объемы.

Трудный вопрос, но у нас есть верный друг компьютер, что он подскажет? (слайд №10), запись в тетрадь.

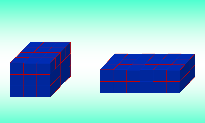
2. № 941. Математика – 5.Зубарева И.И., Мордкович А.Г. Приведите контр пример для утверждения: из любых двух прямоугольных параллелепипедов меньшую площадь поверхности имеет тот, у которого меньший объем. Попробуйте, подберите числа для измерений параллелепипеда. Опять нас выручает компьютер ( слайд № 11) и запись в тетрадь..

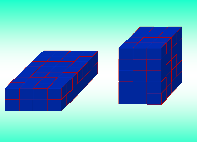
3. Давайте рассмотрим формулу объема параллелепипеда V = abc, какую величину мы

находим произведением ab ? Правильно, площадь донышка, математики еще говорят «площадь основания», поэтому формулу объема параллелепипеда можно записать по – другому ( слайд № 12)

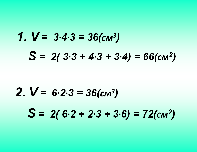
7. Контроль и проверка знаний.

Решение задач из контрольных вопросов Главы V, Математика – 5.Зубарева И.И., Мордкович А.Г. зависимости от оставшегося времени и работоспособности класса.

8. Подведение итогов урока.

С каким важным свойством куба и прямоугольного параллелепипеда мы познакомились?

[ У этих тел есть объем]

Какими единицами измеряется объем тел?

Что такое кубический сантиметр?

Что нужно сделать, чтобы найти объем куба?

[ Возвести длину стороны в куб]

Что нужно сделать, чтобы найти объем параллелепипеда?

Перемножить его измерения]

9. Домашнее задание: №№ 939, 942, 943